在排序数组中查找元素的第一个和最后一个位置

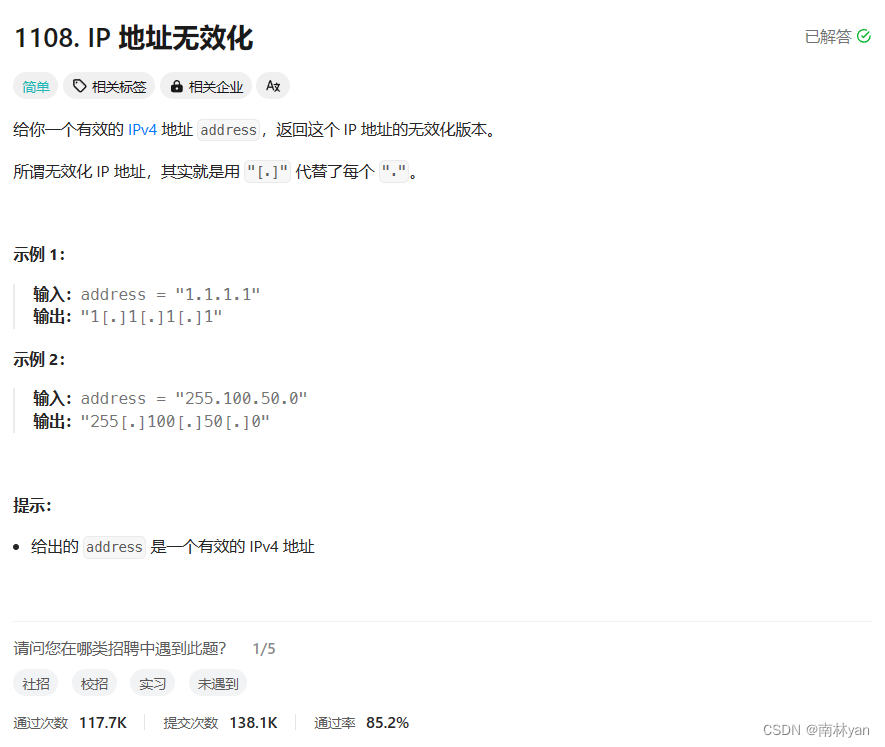
题目

在排序数组中查找元素的第一个和最后一个位置

解法一

class Solution {
   
public:
    vector<int> searchRange(vector<int>& nums, int target) {
   
        int size = nums.size();
        
        //先考虑边界条件
        if(size == 0) return {
   -1, -1};
        if(nums[0] > target || nums[size-1] < target) return {
   -1, -1};

        int left = -1, right = size;
         //直接从左端开始遍历，找到第一个和target相等的就是开始位置
        do
            left++;
        while(nums[left] != target && left < size-1); // left < size-1 可以防止越界

        //直接从右端开始遍历，找到第一个和target相等的就是结束位置
        do  
            right--;
        while(nums[right] != target && right >= 1);   
        
            
        // 可能出现left和right遍历一遍都没有找到目标位置的情况，所以需要判断，此时用nums[left]还是nums[right]都可以
        if(nums[left] == target)
            return {
   left, right};
        else
            return {
   -1, -1};
    }
};

解法二（二分查找）

代码展示

class Solution {
   
public:
    vector<int> searchRange(vector<int>& nums, int target) {
   
        int size = nums.size();
        //处理边界问题
        if(size == 0) return {
   -1, -1};
        int begin=-1, end=-1;
        // 找二分左端点
        int left = 0, right = size-1;
        while(left < right)
        {
   
            int mid = left+(right-left)/2;
            if(nums[mid] < target) left = mid+1;
            else right = mid; 
        }
        if(nums[left] == target) begin = left;
        else return {
   -1, -1};

        //找二分右端点
        left = 0, right = size-1;
        while(left < right)
        {
   
            int mid = left+(right-left+1)/2;
            if(nums[mid] <= target) left = mid;
            else right = mid-1; 
        }
        if(nums[right] == target) end = right;
        else return {
   -1, -1};


        return {
   begin, end};
    }
};

原理剖析

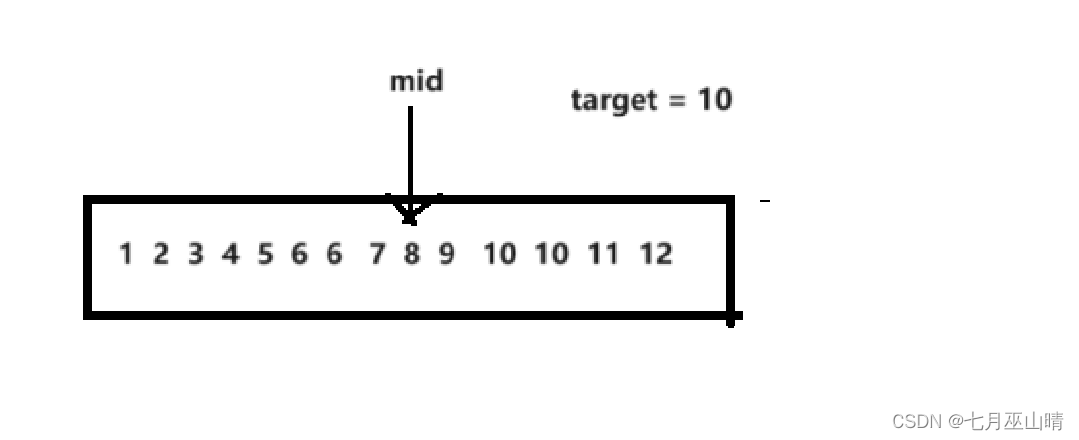
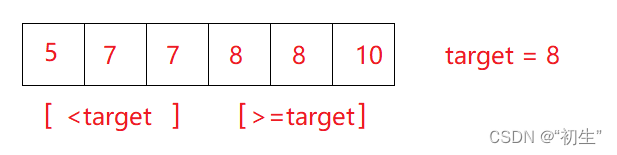
   二分查找需要通过得出这道题目所包含的二段性，来一步一步缩小范围，找到目标值，这道题一个关键的条件就是数组是非递减的，也就意味着数组是递增或者是相等的。二段性怎么找到呢？

   若要找到target，取中心位置为mid，那么就会立刻排出掉一半无关的值，然后再令left=mid,即可缩小排查范围。这样就可以发现这道题使用二分查找来解题的二段性。

首先确定循环结束条件
有两种选择：

1. while(left < right)
2. while(left <= right)

区别就在于是否需要当left == right时再进行判断。

1. 当left == right时， 已经找到了左端点或是右端点，此时不需要冗余的在进行。
2. 第二点原因之后解释。
   所以选择第一点更为合理。

利用二分找到左端点

1. 当nums[mid] < target时， 左端点在右半部分，所以left = mid+1;
2. 当nums[mid] > target时, 左端点在左半部分，所以right = mid-1
3. 当nums[mid] == target时，此时左端点就在left和right之间，此时不能移动left, 因为也许左端点就在mid的左边，也不能将right移动到mid的左边，因为这两种操作都会使得左端点在二分缩小里面被错过。所以可以移动right， 此时right = mid;。
4. 可以将2,3合并，得到若nums[mid] >= target， right = mid;。

利用二分找到右端点

1. 当nums[mid] < target时， 右端点在右半部分，所以left = mid+1;
2. 当nums[mid] > target时, 右端点在左半部分，所以right = mid-1
3. 当nums[mid] == target时，此时右端点就在left和right之间，此时不能移动right, 因为也许右端点就在mid的左边，也不能将right移动到mid的左边，因为这两种操作都会使得左端点在二分缩小里面被错过。所以可以移动right， 此时left = mid;。
4. 可以将1,3合并，得到若nums[mid] <= target， left = mid;。

while(left <= right)导致的死循环问题
   因为当left==right时， 无论是找左端点还是右端点，left 和 right依旧指向mid，永远不会改变，因此如果while(left <= right)的话，就会导致死循环。

mid的取值问题
   通过代码可以看到，mid的取值有两种，分别是：

1. mid = left+(right-left)/2;
2. mid = left+(right-left+1)/2;

   由于是二分，都是除二，所以上面1代表的意思就是二分后向下取整，2代表的意思就是向上取整。
   下面来看找二分右端点的特殊情况;

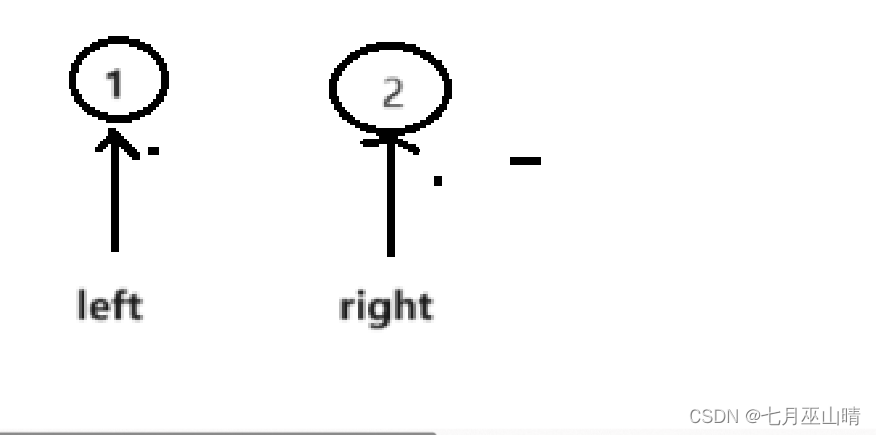
   若现在left和right的指向如上图所示，若是mid取值：mid = left+(right-left)/2;,则mid位于1处， 若target就是1， 此时执行的是if(nums[mid] <= target) left = mid;,就会导致left一直指向1，right一直指向不变，没有left<right,while循环就不会结束，就会造成死循环。所以得向上取整，此时mid位于2处， 就不会触发死循环。找左端点使用mid = left+(right-left)/2的原因也是如此。

    😄 创作不易，你的点赞和关注都是对我莫大的鼓励，再次感谢您的观看😄