一.二分查找
目前有一个有序数列,举个例子,假设是1~1000,让我们去查找931这个数字,浅显且暴力的做法就是直接从头到尾遍历一遍,直到找到931为止。当n非常大,比如达到100w时,这是一个非常大的量级,考虑到效率的优劣这是不能接收的。
二分查找是基于有序序列的一种查找算法,所谓的有序是序列严格递增:每次根据当前查找区间的中位数来判断是否与目标相同,如果不同就根据当前大小以上个区间的中点作为区间的某一端,继续执行这个二分查找过程~
高效的点在于,二分的每一步都可以去除区间中一半的元素,其时间复杂度是O(logn),学过数学的各位理科生都知道,对数的增加速度是非常慢的,甚至小于一次的幂函数,当N非常大的时候,越能体会到logN复杂度的含金量!

话不多说直接上代码,依旧是博主自研的vector函数版:
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void BinarySearch(vector<int> V,int x){
int left=0;
int right=V.size()-1; //数组的末位
int i=(left+right)/2; //初始中点
int flag=0;// flag为0意味着未查询到
while(flag==0&&left<=right)
{
cout<<"当前查询的元素下标为:"<<i<<endl;
if(V[i]==x)
{
cout<<i<<"位即为x的值~";
flag=1;
}
else if(x>V[i]) //目标大于当前中点,中点的右一位+1作为新区间的左端点
{
left=i+1;
i=(left+right)/2;
}
else if(x<V[i])//目标小于当前中点,中点的左一位-1作为新区间的左端点
{
right=i-1;
i=(left+right)/2;
}
}
if(flag==0)
cout<<"很遗憾,未找到~"<<endl;
}
int main() {
int n=0;
vector<int> V;
cout<<"请输入数列规模:"<<endl;
cin>>n;
for(int i=1;i<=n;i++) //读入数据
{
int temp=0;
cin>>temp;
V.push_back(temp);
}
sort(V.begin(),V.end());//排序一下,保证V本身有序!
//其实这种题目直接就是有序~
int x=0;
cout<<"请输入待查询的值:"<<endl;
cin>>x;
BinarySearch(V,x);
return 0;
}以书上的测试用例作为验证组:
10
3 7 8 11 15 21 33 52 66 88
11
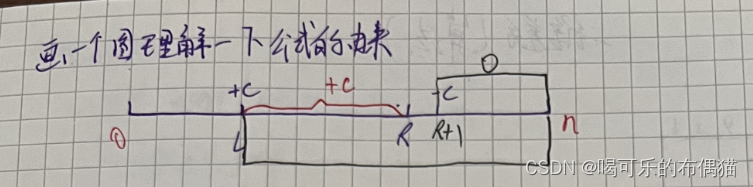
首先给大家图解画一下过程,其实不难想象:

测试结果如下,没什么bug:

tips:如果各位是考试或者写什么数构的伪码,其实用普通的数组就行,博主在实现的时候偏爱使用vector——这种随时可以扩展的数组(向量)属实给人极大的安全感,各位在阅读的时候不要见怪~
升级问题,假设序列中有多个相同的元素,请用二分法找到这个区间?(格式为左开右闭~)
其实和之前差不多,区别在于,我们要找到该元素第一次和最后一次出现的位置,因此之前的大小比较应该做出改善,如下:
- 找左端点时,还是用mid来与目标值对比,如果mid值大于等于目标值,则说明目标值第一次出现的位置有可能还要往左,因此还要往左查询,因此要令right=mid(向左缩小范围~);如果mid比目标值小,则说明目标值第一次出现的位置还要再往右,应该令left=mid+1
- 找右端点时,如果mid>x,说明最后的目标数x在mid处或者mid的左侧,因此应该在left~mid里面继续找,即right=mid;如果mid小于等于x,说明最后一个x一定在mid的右侧,因此令left=mid+1
- 其实两者改变区间的方式一致,区别就在于改变的条件~
先是找左端点的函数:
int FindLeft(vector<int> V,int x){
int left=0;
int right=V.size()-1; //数组的末位
int i=(left+right)/2; //初始中点
while(left<right)
{
//cout<<"当前查询的元素下标为:"<<i<<endl;
if(V[i]>=x) //如果当前值大于等于目标值,说明最小的有可能是mid或者mid的左边
{
right=i;
i=(left+right)/2;
}
else if(V[i]<x)
{
left=i+1;//如果当前值小于目标值,说明最小的还要再往右
i=(left+right)/2;
}
}
return left;
}然后是找右端点的函数:
int FindRight(vector<int> V,int x){
int left=0;
int right=V.size()-1; //数组的末位
int i=(left+right)/2; //初始中点
while(left<right)
{
//cout<<"当前查询的元素下标为:"<<i<<endl;
if(V[i]>x) //如果当前值大于等于目标值,说明最大的有可能是mid或者mid的左边
{
right=i;
i=(left+right)/2;
}
else if(V[i]<=x)
{
left=i+1;//如果当前值小于目标值,说明最大的可能还要再往右
i=(left+right)/2;
}
}
return right;
}最后main函数调用:
int main() {
int n=0;
vector<int> V;
cout<<"请输入数列规模:"<<endl;
cin>>n;
for(int i=1;i<=n;i++) //读入数据
{
int temp=0;
cin>>temp;
V.push_back(temp);
}
sort(V.begin(),V.end());//排序一下,保证V本身有序!
//其实这种题目直接就是有序~
int x=0;
cout<<"请输入待查询的值:"<<endl;
cin>>x;
cout<<x<<"的存在区间是:"<<endl;
cout<<"["<<FindLeft(V,x)<<","<<FindRight(V,x)<<")"<<endl;
return 0;
}两组测试用例:
- 【1,2,2,2,3,3,3,3,3,4】——3
- 【0,0,0,1,2,2,2,2,3,3】——2


没什么bug~
tips:其实写成双闭区间也可以,一个道理~修改一下if条件即可
一些注意事项:
- 在程序设计时,二分更多用的是非递归的设计方法
- 当上界超越int范围的一半时,计算中点的left+right这一算式可能会导致溢出,这里修改的策略是mid=left+(right-left)/2
- 上面找左右端点的时候,需要将条件改为left<mid,不然会造成死循环
进一步思考上一步中寻找区间端点的过程:本质上,所有需要用到二分法的题目都是在解决:寻找有序序列中第一个满足某条件元素的位置~

如上,核心点就在于修改判断的条件,这个条件,在序列中一定是从左到右先不满足,然后满足的过程~
二.应用
1.方程根的近似值
先来看一个简单的例子:求出根号n的近似值,也就是sqrt(n)。
与其用mid和sqrt(n)比,不如直接用mid平方和n比,再对mid开方,不难发现,这也是一个二分查找~
直接上代码:
#include <iostream>
#include <cmath>
using namespace std;
void Calsqrt(int x)
{
double n1=sqrt(x);
cout<<x<<"的真实开根号值为:"<<n1<<endl;
double left=trunc(n1),right=trunc(n1)+1;
cout<<x<<"的取值范围是:["<<left<<","<<right<<"]"<<endl;
double i=0;
while(right-left>0.0001) //设置精度
{
i=(left+right)/2;//初始中点
if((i*i)>x) //目标大于待查找值,所以将上一个值作为右端点,查询区间左移
right=i;
else //目标小于待查找值,所以将上一个值作为左端点,查询区间右移
left=i;
}
cout<<i<<endl;
}
int main() {
int n=0;
cout<<"请输入n的值:";
cin>>n;
Calsqrt(n);
return 0;
}注意点:
- 与真正的二分查找相比,本次的二分其实是针对一个连续的函数,因此所谓的left和right一定要为double型的,不然无效且死循环
- 同样的道理,在改变区间时,直接用left或者right与mid相等就行——考过考研数学一的道友肯定知道,对于连续性的函数,端点处划分到哪个区间都不影响!
2.装水问题

如上,其实还是一个同样的问题,关键要找到一个切入点:随着水高度h的增加,面积S是不断增加的——这符合二分要求序列递增的前提!
因此我们可以对h进行二分,并计算当前h下的面积与目标面积的差距,然后还是左右移动二分区间的套路,即可解决~
#include <iostream>
#include <cmath>
using namespace std;
#define Pi 3.14
void CalH(double R,double r)
{
double sq1=R*R*Pi;//原始面积
double sq2=sq1*r;//目标面积
double answer=sq2/Pi;//设置一个中间值为目标h的平方倍
double i=0; //二分中点
double left=0,right=R;// 二分区间
while(right-left>0.0001&&r<=1) //设置精度 ,比例不能超过1
{
i=(left+right)/2;//初始中点
if((i*i)>answer) //目标大于待查找值,所以将上一个值作为右端点,查询区间左移
right=i;
else //目标小于待查找值,所以将上一个值作为左端点,查询区间右移
left=i;
}
cout<<"目标h的值为:"<<i<<endl;
}
int main() {
double R=0,r=0;
cout<<"请输入半径的值:"<<endl;
cin>>R;
cout<<"请输入比例的值:"<<endl;
cin>>r;
CalH(R,r);
return 0;
}这里我们选一个测试用例检测一下:

没什么问题~

3.木棒切割问题

还是老套路:找到递增和目标值,两个条件直接选用二分!
不难发现,当每一根木棒的长度越大时,分出来的个数肯定越小,因此应该用当前单体长度来进行二分,从小到大——当对应木棒的个数不符合题意中要求的个数时,则结束二分。
直接上代码:
#include <iostream>
#include <vector>
#include <cmath>
using namespace std;
int Cut(vector<int>V,int k) //当前长度最多在数组中切多少~
{
int count=0;
for(int i=0;i<=V.size()-1;i++)
{
int temp=0;
temp=V[i]/k;
count+=temp;
}
return count;
}
void CalN(vector<int> V,int k)
{
int min=V[0];
for(int i=1;i<=V.size()-1;i++)
if(V[i]<min)
min=V[i];
//找出最小值作为二分区间的右端点
int left=1,right=min;//最短也要长度为1,最长也超不过单体的最短~
int i=0; //二分中点
while(right-left>1) //当差距是一位时,说明已经找到了,由于向下取整的原因会造成死循环,因此此时可以直接输出中点的值
{
i=(left+right)/2;//初始化中点
if(Cut(V,i)>=k) //如果当前长度下的段数比目标的多,说明每一段的长度还可以再长,因此区间右移
left=i;
else //如果当前的比目标的还少,应该缩短每一段的长度来增加个数,使得满足要求~
right=i;
}
cout<<"最大长度为:"<<i<<endl;
}
int main() {
int num=0;
vector<int> V;
cout<<"请输入木棒的个数:"<<endl;
cin>>num;
cout<<"请输入每段木棒的长度:"<<endl;
for(int i=1;i<=num;i++)
{
int temp=0;
cin>>temp;
V.push_back(temp);
}
int K=0;
cout<<"请输要求长度相等的木棒个数:"<<endl;
cin>>K;
CalN(V,K);
return 0;
}测试就用书上的测试两次:

和手算的结果一致,没什么问题:

三.快速幂
快速幂,顾名思义,一种快速计算幂函数的方法。博主的个人理解是,这玩意既像二分的思想,又像递归的思想,因此也可以称之为二分幂~
现有数2的10000000次方,我们当然不能把2累乘10000000次——这是相当失败的程序。其实中间有很多步骤可以省略:
- 当指数是偶数时,我们可以让指数除以2,底数乘以底数;
- 当指数是奇数时,我们可以将指数变为偶数;
举个例子,2的10次方,使用快速幂的思想,计算过程如下:
- 2的10次方,10是偶数,此时待算式为:4的5次
- 5为奇数,因此待算式为:4*4的4次
- 4为偶数,因此待算式为:4*16的2次
- 2为偶数,因此待算式为:4*16*256的一次
- 1为奇数,因此待算式为:4*16*256*256的0次,直接计算出来~
不难发现,上述过程只需要5步,而累乘需要10步,当指数变得非常大时,这一优势会愈加明显~
代码如下:
1.非递归形态
#include<iostream>
using namespace std;
long long fpow(long long a,long long b){//a是底数,b是指数
long long ans=1;//初始化答案为1
while(b){//当指数不为0时执行
if(b%2==0){//指数为偶数时,指数除以2,底数乘以底数
b/=2;
a*=a;
}else{//指数为奇数时,分离指数,ans乘以底数
ans*=a;
b--;
}
}
return ans;
}
int main(){
long long n,m;
cin>>n>>m;
cout<<fpow(n,m)<<endl;
}2.递归形态
#include<iostream>
using namespace std;
typedef long long LL;
LL binaryPow(LL a,LL b)
{
if(b==0) //递归边界——即0次方
return 1;
if(b%2==1) //奇偶各一次递归式
return a*binaryPow(a,b-1);
else{
LL mul =binaryPow(a,b/2);
return mul*mul;
}
}
int main(){
long long n,m;
cin>>n>>m;
cout<<binaryPow(n,m)<<endl;
}tips:写在最后
- 对于二分法的使用时机,主要要看两个点:需要找到某个数值第一次或者最后一次出现的位置,且在寻找这个值的过程中,满足该值单调递增(递减)
- 二分的循环条件,基本上都是right>left,或者作差大于某个值~
- 文中基本上全是博主根据伪码自创的实现方式,博主酷爱使用vector,可能有些朋友看起来比较吃力;此外所有的mid都写成了i,大家看的时候尽量理解~