前言
更好的阅读体验:https://blog.dwj601.cn/GPA/4th-term/OptMethod/
教材情况:
| 课程名称 | 选用教材 | 版次 | 作者 | 出版社 | ISBN号 |
|---|---|---|---|---|---|
| 最优化算法 | 最优化方法 | 2 | 孙文瑜 | 高等教育出版社 | 978-7-04-029763-8 |
第一章 基本概念
1.1 最优化问题简介
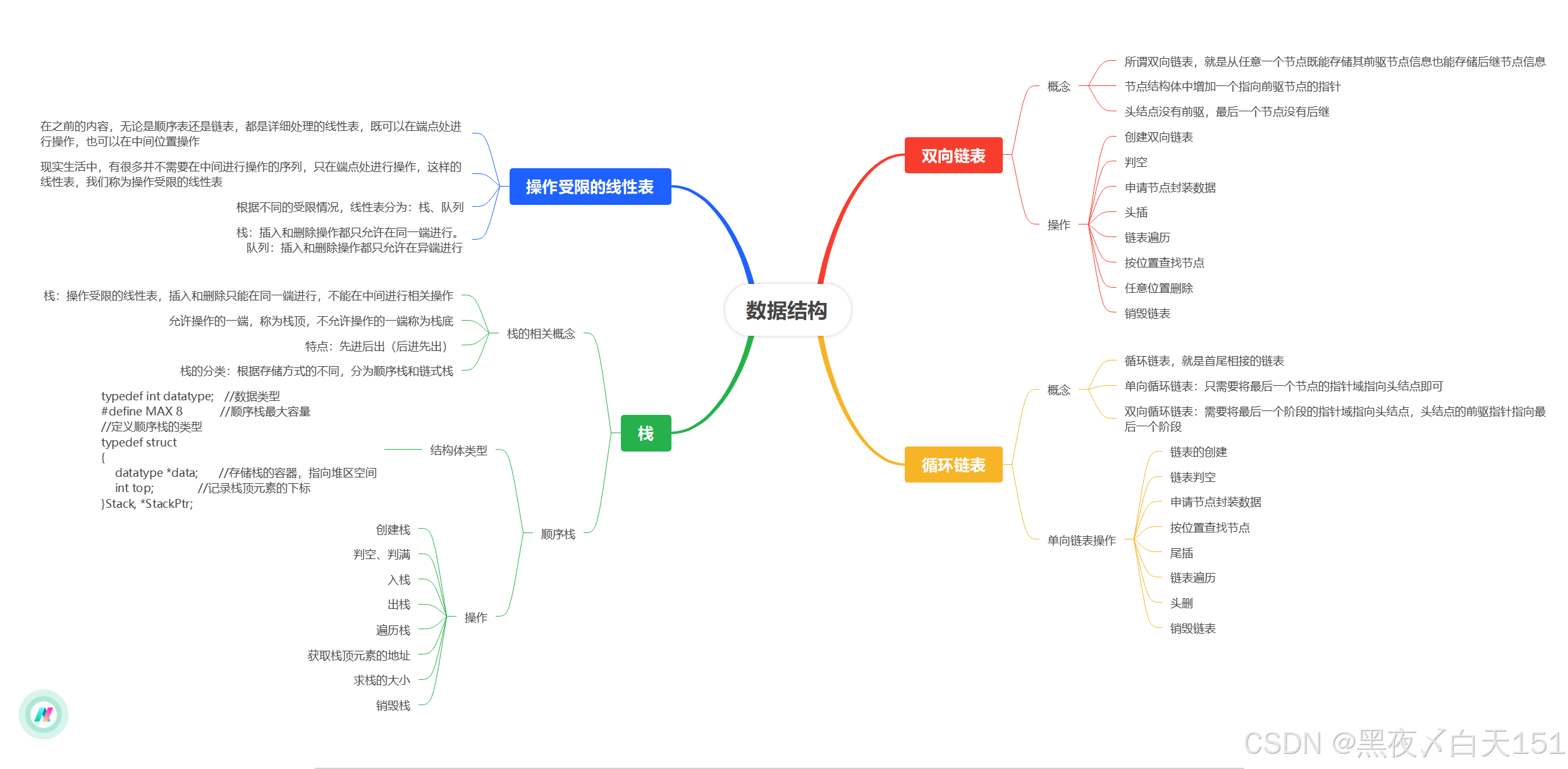
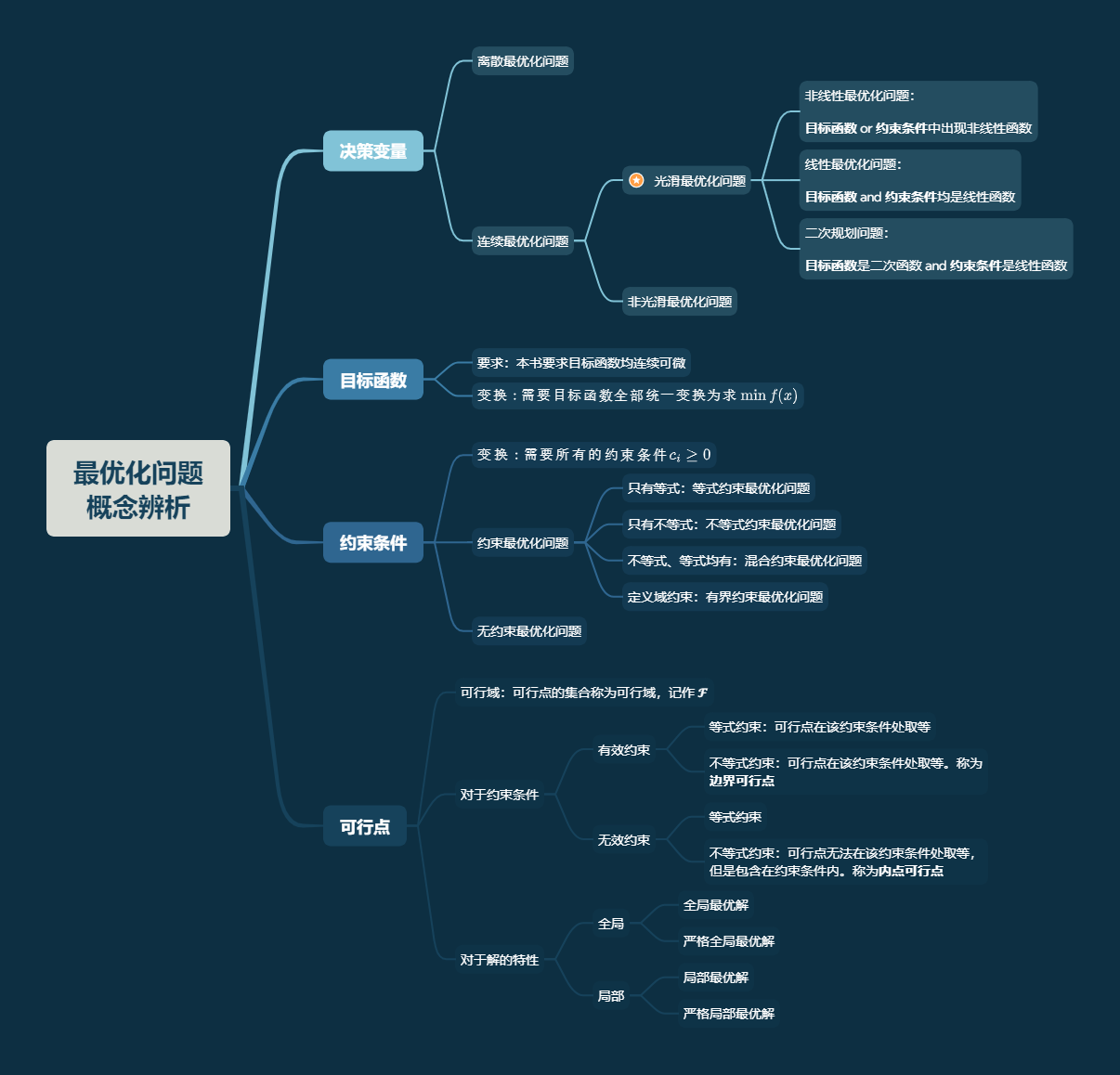
本目主要讲解最优化问题的一些分类,下附脑图(由 Xmind 软件制作):
{% fold light @分类脑图 %}
{% endfold %}
1.2 凸集和凸函数
{% note light %}
由于本书介绍的最优化求解方法一般只适用于求解局部最优解,那么如何确定全局最优解呢?以及如何确定唯一的全局最优解呢?本目揭晓答案:
( 唯一 ) 全局最优解 = 局部最优解 + ( 严格 ) 凸目标函数 + 凸可行域 (\text{唯一})\text{全局最优解}=\text{局部最优解}+(\text{严格})\text{凸目标函数}+\text{凸可行域} (唯一)全局最优解=局部最优解+(严格)凸目标函数+凸可行域
其中凸可行域包含于凸集,凸目标函数包含于凸函数,凸目标函数+凸可行域的问题称为凸规划问题。因此本目将分别介绍凸集、凸函数和凸规划三个概念。
{% endnote %}
1.2.1 凸集
凸集的定义:若集合中任意两点的线性组合都包含于集合,则称该集合为凸集。符号化即:
∀ x , y ∈ D ∧ λ ∈ [ 0 , 1 ] s . t . λ x + ( 1 − λ ) y ∈ D \begin{aligned} \forall \quad x,y \in D \ \land \ \lambda \in [0,1] \\ s.t. \quad \lambda x+(1-\lambda)y \in D \\ \end{aligned} ∀x,y∈D ∧ λ∈[0,1]s.t.λx+(1−λ)y∈D
凸集的性质:设 D 1 , D 2 ⊂ R n D_1,D_2 \subset R^n D1,D2⊂Rn 均为凸集(下列 x , y x,y x,y 均表示向量),则:
- 两凸集的交 D 1 ∩ D 2 = { x ∣ x ∈ D 1 ∧ x ∈ D 2 } D_1 \cap D_2 = \{x\ |\ x \in D_1 \land x \in D_2\} D1∩D2={x ∣ x∈D1∧x∈D2} 是凸集
- 两凸集的和 D 1 + D 2 = { x , y ∣ x ∈ D 1 , y ∈ D 2 } D_1 + D_2 = \{x,y\ |\ x \in D_1 , y \in D_2\} D1+D2={x,y ∣ x∈D1,y∈D2} 是凸集
- 两凸集的差 D 1 − D 2 = { x , y ∣ x ∈ D 1 , y ∈ D 2 } D_1 - D_2 = \{x,y\ |\ x \in D_1 , y \in D_2\} D1−D2={x,y ∣ x∈D1,y∈D2} 是凸集
- 对于任意非零实数 α \alpha α,集合 α D 1 = { α x ∣ x ∈ D 1 } \alpha D_1 = \{ \alpha x \ |\ x \in D_1 \} αD1={αx ∣ x∈D1} 是凸集
{% fold light @证明 %}

{% endfold %}
凸集的应用
刻画可行域
凸组合定义
设 x ( 1 ) , x ( 2 ) , ⋯ , x ( p ) ∈ R n , 且 ∑ i = 1 p α i = 1 ( a i ≥ 0 ) s . t . x = α 1 x 1 + α 2 x 2 + ⋯ + α p x p 则称 x 为向量 x ( 1 ) , x ( 2 ) , ⋯ , x ( p ) 的凸组合 \begin{aligned} \text{设}\ x^{(1)},x^{(2)}, \cdots, x^{(p)} \in R^n ,\text{且}\ \sum_{i=1}^p \alpha_i = 1(a_i \ge 0) \\ s.t. \quad x = \alpha_1x^1 + \alpha_2x^2 + \cdots + \alpha_px^p \\ \text{则称}\ x\ \text{为向量}\ x^{(1)},x^{(2)}, \cdots, x^{(p)}\ \text{的凸组合} \end{aligned} 设 x(1),x(2),⋯,x(p)∈Rn,且 i=1∑pαi=1(ai≥0)s.t.x=α1x1+α2x2+⋯+αpxp则称 x 为向量 x(1),x(2),⋯,x(p) 的凸组合凸组合定理: D ∈ R n D \in R^n D∈Rn 是凸集的充分必要条件是 D D D 中任取 m m m 个点 x i ( 1 , 2 , ⋯ m ) x^i(1,2,\cdots m) xi(1,2,⋯m) 的凸组合任属于 D D D,即:
∑ i = 1 m α i x i ∈ D ( α i ≥ 0 ( i = 1 , 2 , ⋯ , m ) , ∑ i = 1 m α i = 1 ) \sum_{i=1}^m \alpha_ix_i \in D\left( \alpha_i \ge 0(i=1,2,\cdots,m),\sum_{i=1}^m \alpha_i = 1 \right) i=1∑mαixi∈D(αi≥0(i=1,2,⋯,m),i=1∑mαi=1){% fold light @凸组合定理证明 %}

{% endfold %}
分析最优解的最优性条件
超平面定义(凸集分离定理):设 D 1 , D 2 ⊂ R n D_1,D_2 \subset R^n D1,D2⊂Rn 为两非空凸集,若存在非零向量 α ∈ R n \alpha \in R^n α∈Rn 和实数 β \beta β,使得
D 1 ⊂ H + = { x ∈ R n ∣ α T x ≥ β } D 2 ⊂ H − = { x ∈ R n ∣ α T x ≤ β } \begin{aligned} D_1 \subset H^+ = \{ x \in R^n \ | \ \alpha^T x \ge \beta\} \\ D_2 \subset H^- = \{ x \in R^n \ | \ \alpha^T x \le \beta\} \end{aligned} D1⊂H+={x∈Rn ∣ αTx≥β}D2⊂H−={x∈Rn ∣ αTx≤β}
则称超平面 H = { x ∈ R n ∣ α T x = β } H = \{ x \in R^n \ | \ \alpha^Tx=\beta \} H={x∈Rn ∣ αTx=β} 分离集合 D 1 D_1 D1 和 D 2 D_2 D2,严格分离时上述不等式无法取等投影定理:设 D ∈ R n D \in R^n D∈Rn 是非空闭凸集, y ∈ R n y \in R^n y∈Rn 但 y ∉ D y \notin D y∈/D,则
( 1 ) 存在唯一的点 x ‾ ∈ D , 使得集合 D 到点 y 的距离最小 ( 2 ) x ‾ ∈ D 是点 y 到集合D的最短距离点的充分必要条件为 : ∀ x ∈ D , < x − x ‾ , y − x ‾ > ≤ 0 \begin{align*} (1)& \text{存在唯一的点} \ \overline x \in D,\text{使得集合}D\text{到点} y \text{的距离最小} \\ (2)& \overline x \in D \text{是点} y \text{到集合D的最短距离点的充分必要条件为}:\forall x \in D,<x-\overline x,y - \overline x> \le 0 \end{align*} (1)(2)存在唯一的点 x∈D,使得集合D到点y的距离最小x∈D是点y到集合D的最短距离点的充分必要条件为:∀x∈D,<x−x,y−x>≤0
1.2.2 凸函数
凸函数的定义:设函数 f ( x ) f(x) f(x) 在凸集 D D D 上有定义
- 若 ∀ x , y ∈ D 和 λ ∈ [ 0 , 1 ] \forall x,y \in D\ \text{和}\ \lambda \in [0,1] ∀x,y∈D 和 λ∈[0,1] 有 f ( λ x + ( 1 − λ ) y ) ≤ λ f ( x ) + ( 1 − λ ) f ( y ) f(\lambda x + (1-\lambda)y) \le \lambda f(x) + (1-\lambda)f(y) f(λx+(1−λ)y)≤λf(x)+(1−λ)f(y),则称 f ( x ) f(x) f(x) 是凸集 D D D 上的凸函数
- 若 ∀ x , y ∈ D 和 λ ∈ ( 0 , 1 ) \forall x,y \in D\ \text{和}\ \lambda \in (0,1) ∀x,y∈D 和 λ∈(0,1) 有 f ( λ x + ( 1 − λ ) y ) < λ f ( x ) + ( 1 − λ ) f ( y ) f(\lambda x + (1-\lambda)y) < \lambda f(x) + (1-\lambda)f(y) f(λx+(1−λ)y)<λf(x)+(1−λ)f(y),则称 f ( x ) f(x) f(x) 是凸集 D D D 上的严格凸函数
凸函数的性质:
- 如果 f f f 是定义在凸集 D D D 上的凸函数,实数 α ≥ 0 \alpha \ge 0 α≥0,则 α f \alpha f αf 也是凸集 D D D 上的凸函数
- 如果 f 1 , f 2 f_1,f_2 f1,f2 是定义在凸集 D D D 上的凸函数,则 f 1 + f 2 f_1+f_2 f1+f2 也是凸集 D D D 上的凸函数
- 如果 f i ( x ) ( i = 1 , 2 , ⋯ , m ) f_i(x)(i=1,2,\cdots,m) fi(x)(i=1,2,⋯,m) 是非空凸集 D D D 上的凸函数,则 f ( x ) = max 1 ≤ i ≤ m ∣ f i ( x ) ∣ f(x) = \max_{1 \le i \le m} |f_i(x)| f(x)=max1≤i≤m∣fi(x)∣ 也是凸集 D D D 上的凸函数
- 如果 f i ( x ) ( i = 1 , 2 , ⋯ , m ) f_i(x)(i=1,2,\cdots,m) fi(x)(i=1,2,⋯,m) 是非空凸集 D D D 上的凸函数,则 f ( x ) = ∑ i = 1 m α i f i ( x ) ( α i ≥ 0 ) f(x) = \displaystyle \sum_{i=1}^m \alpha_i f_i(x)\quad(\alpha_i \ge 0) f(x)=i=1∑mαifi(x)(αi≥0) 也是凸集 D D D 上的凸函数
{% fold light @凸函数的性质证明 %}


{% endfold %}
凸函数的判定定理:
函数值角度:函数 f ( x ) f(x) f(x) 是 R n R^n Rn 上的凸函数的充分必要条件是 ∀ x , y ∈ R n \forall x,y \in R^n ∀x,y∈Rn,单变量函数 ϕ ( α ) = f ( x + α y ) \phi(\alpha)=f(x + \alpha y) ϕ(α)=f(x+αy) 是关于 α \alpha α 的凸函数
{% fold light @凸函数的判别定理证明:函数值角度 %}

{% endfold %}一阶梯度角度:设 f ( x ) f(x) f(x) 是定义在非空开凸集 D D D 上的可微函数,则:
- f ( x ) f(x) f(x) 是 D D D 上凸函数的充分必要条件是: f ( y ) ≥ f ( x ) + ∇ f ( x ) T ( y − x ) , ∀ x , y ∈ D f(y) \ge f(x)+\nabla f(x)^T(y-x), \quad \forall x,y \in D f(y)≥f(x)+∇f(x)T(y−x),∀x,y∈D
- f ( x ) f(x) f(x) 是 D D D 上严格凸函数的充分必要条件是: f ( y ) > f ( x ) + ∇ f ( x ) T ( y − x ) , ∀ x , y ∈ D , x ≠ y f(y) > f(x)+\nabla f(x)^T(y-x), \quad \forall x,y \in D,\quad x \ne y f(y)>f(x)+∇f(x)T(y−x),∀x,y∈D,x=y
{% fold light @凸函数的判别定理证明:一阶导数角度 %}
无需掌握证明,但是为了便于理解性记忆,可以从二次凸函数进行辅助理解记忆。

{% endfold %}二阶梯度角度:设 f ( x ) f(x) f(x) 是定义在非空开凸集 D D D 上的二阶可微函数,则:
- f ( x ) f(x) f(x) 是 D D D 上凸函数的充分必要条件是:海塞矩阵正半定
- f ( x ) f(x) f(x) 是 D D D 上严格凸函数的充分必要条件是:海塞矩阵正定?其实不一定,例如 x 4 x^4 x4 是严格凸函数,但是其海塞矩阵是正半定的并非正定。因此更严谨的定义应该是:海塞矩阵正定的是严格凸函数,严格凸函数的海塞矩阵是正半定的。
1.2.3 凸规划(个人补充)
本目为个人补充内容,用于整合上述 1.2.1 与 1.2.2 内容。我们知道,学习凸集和凸函数的终极目标是为了求解凸规划问题,凸规划问题可以简述为 凸可行域 + 凸目标函数 + 局部最优解 = 全局最优解,那么如何证明这个定理是正确的呢?局部最优解求出来以后,目标函数也确定为凸函数以后,如何确定可行域是凸集呢?下面揭晓:
证明凸规划问题的正确性
定理:在可行域是凸集,目标函数非严格凸的情况下,局部最优解 x ∗ x^* x∗ 也是全局最优解
{% fold light @证明(反证法) %}

{% endfold %}定理:在可行域是凸集,目标函数是严格凸的情况下,局部最优解 x ∗ x^* x∗ 也是唯一的全局最优解
{% fold light @证明(反证法) %}

{% endfold %}
确定可行域是否为凸集
定理:若约束条件 c i ( x ) ≥ 0 c_i(x) \ge 0 ci(x)≥0 中每一个约束函数 c i ( x ) c_i(x) ci(x) 都是凹函数,则可行域 F F F 是凸集
{% fold light @证明 %}

{% endfold %}定理:若约束条件 c i ( x ) ≤ 0 c_i(x) \le 0 ci(x)≤0 中每一个约束函数 c i ( x ) c_i(x) ci(x) 都是凸函数,则可行域 F F F 是凸集
{% fold light @证明 %}

{% endfold %}定理:若约束条件中每一个约束函数 c i ( x ) c_i(x) ci(x) 都恒等于零,则可行域 F F F 是凸集
{% fold light @证明 %}

{% endfold %}
1.3 最优性条件
{% note light %}
最优性条件是指最优化问题的最优解所必须满足的条件,本目介绍求解无约束最优化问题的一阶必要条件和二阶必要条件,再补充介绍二阶充分条件以及针对凸规划问题的二阶充分必要条件。最后简单介绍求解等式约束最优化问题的拉格朗日乘子法。
{% endnote %}
1.3.1 下降方向
在开始之前先简单介绍一下「下降方向」这个概念。
下降方向定义:设 f ( x ) f(x) f(x) 为定义在空间 R n R^n Rn 的连续函数,点 x ˉ ∈ R n \bar x \in R^n xˉ∈Rn,若对于方向 s ∈ R n s \in R^n s∈Rn 存在数 δ > \delta > δ> 0 使
f ( x ˉ + α s ) < f ( x ˉ ) , ∀ α ∈ ( 0 , δ ) f(\bar x+\alpha s) < f(\bar x),\quad \forall \alpha \in (0,\delta) f(xˉ+αs)<f(xˉ),∀α∈(0,δ)
成立,则称 s s s 为 f ( x ) f(x) f(x) 在 x ˉ \bar x xˉ 处的一个下降方向。在 点 x ˉ \bar x xˉ 处的所有下降方向的全体记为 D ( x ˉ ) D(\bar x) D(xˉ)下降方向定理:设函数 f ( x ) f(x) f(x) 在点 x ˉ \bar x xˉ 处连续可微,如存在非零向量 s ∈ R n s \in R^n s∈Rn 使
∇ f ( x ˉ ) T s < 0 \nabla f(\bar x)^Ts < 0 ∇f(xˉ)Ts<0
成立,则 s s s 是 f ( x ) f(x) f(x) 在点 x ˉ \bar x xˉ 处的一个下降方向{% fold light @证明 %}

{% endfold %}
1.3.2 充分必要条件
设 f : D ⊂ R n → R 1 f:D \subset R^n \to R^1 f:D⊂Rn→R1 是定义在开集 D D D 上的函数, x ∗ ∈ D x^* \in D x∗∈D 是该函数的局部极小点, f ( x ) f(x) f(x) 的一阶导数 g ( x ) = ∇ f ( x ) g(x)=\nabla f(x) g(x)=∇f(x),二阶导数 G ( x ) = ∇ 2 f ( x ) G(x)=\nabla ^2f(x) G(x)=∇2f(x)。
一阶必要条件。若目标函数在定义域 D 上连续可微,则 x ∗ x^* x∗ 是局部极小点的一阶必要条件为:
g ( x ∗ ) = 0 g(x^*)=0 g(x∗)=0二阶必要条件。若目标函数在定义域 D 上二阶连续可微,则 x ∗ x^* x∗ 是局部极小点的二阶必要条件为:
g ( x ∗ ) = 0 , G ( x ∗ ) ≥ 0 g(x^*)=0,\quad G(x^*)\ge 0 g(x∗)=0,G(x∗)≥0二阶充分条件。若目标函数在定义域 D 上二阶连续可微,则 x ∗ x^* x∗ 是严格局部极小点的二阶充分条件为:
g ( x ∗ ) = 0 , G ( x ∗ ) 是正定的 g(x^*)=0,\quad G(x^*) \text{是正定的} g(x∗)=0,G(x∗)是正定的充分必要条件(凸最优性定理)。在无约束最优化问题中,如果目标函数是凸的,则 x ∗ x^* x∗ 是全局极小点的充分必要条件是:
g ( x ∗ ) = 0 g(x^*)=0 g(x∗)=0
1.3.3 拉格朗日乘子法
如果现在最优化问题不是单纯的无约束最优化问题,而是增设了等式约束的等式约束最优化问题,如何求解呢?我们引入 Lagrange \text{Lagrange} Lagrange 乘子法,将所有的等式约束都转化到目标函数中得到一个等价的无约束最优化问题,即:
对于这样的等式约束最优化问题:
min f ( x ) s.t. c i ( x ) = 0 , i = 1 , 2 , ⋯ , m . \begin{aligned} \min\quad& f(x)\\ \text{s.t.}\quad&c_i(x)=0,i=1,2,\cdots,m. \end{aligned} mins.t.f(x)ci(x)=0,i=1,2,⋯,m.
引入拉格朗日乘子将其转化为无约束最优化问题,进而利用上述无约束最优化问题的求解策略进行求解:
L ( x , λ ) = f ( x ) − ∑ i = 1 m λ i c i ( x ) L(x,\lambda) = f(x) - \sum_{i=1}^m\lambda_ic_i(x) L(x,λ)=f(x)−i=1∑mλici(x)
1.4 最优化方法概述
现实生活中,对于常见问题的建模往往是极其复杂的,为了求得最优解,我们需要对建立的模型进行微分算子的求解。但是问题是,尽管我们知道最优解一定存在于微分算子的数值解中,但是我们往往不能很快的计算出其数值解,因此我们需要采用别的方法进行计算。最常用的方法就是本书介绍的迭代法。
大概就两步:确定初值开始判断,如果符合条件的约束则停止迭代得到最终的解;如果不符合约束则对当前迭代值赋予修正量并继续迭代判断。直到找到最终的解。接下来将对 5 个专有名词进行解释,分别为:初始点的选取、迭代点好坏的判定、收敛速度、迭代的终止条件、修正量 s ( k ) s^{(k)} s(k) 的确定。
1.4.1 初始点的选取
初始点的选取取决于算法的收敛性能。
- 如果一个算法可以做到全局收敛,则初始点的选取是任意的
- 如果一个算法只能局部收敛,则初始点的选取往往需要尽可能的接近最优解,而这往往是困难的,因为我们并不知道的最优解是什么。此时可以采用借鉴之前的经验来选择初始点
1.4.2 迭代点好坏的判定
判定一个迭代点的好坏时,我们往往会设计一个评价函数,而评价函数的设计取决于约束问题的种类。
- 对于无约束最优化问题。我们可以直接将目标函数 f ( x ) f(x) f(x) 设计为评价函数。很显然,如果一个迭代点对应的的函数值比之前点对应的函数值更小,则可以说明当前迭代点由于之前的点
- 对于有约束最优化问题。此时我们不仅仅需要考虑函数值的大小,也要考虑当前迭代点的可行程度(离可行域的距离)。因此此类最优化问题往往既包含目标函数,也包含约束函数。
1.4.3 收敛速度
若当前算法一定收敛,我们还需要判断收敛的速度,接下来介绍收敛的速度。
假设
- 设向量序列 { x ( k ) ⊂ R n } \{ x^{(k)} \subset R^n \} {x(k)⊂Rn} 收敛于 x ∗ x^* x∗
定义
- 误差序列: e k = x ( k ) − x ∗ e_k = x^{(k)} - x^* ek=x(k)−x∗
- 收敛率表达式: lim k → ∞ ∣ ∣ e k + 1 ∣ ∣ ∣ ∣ e k ∣ ∣ r = C \displaystyle \lim_{k \to \infty} \frac{|| e_{k+1} ||}{||e_k||^r} = C k→∞lim∣∣ek∣∣r∣∣ek+1∣∣=C,并称序列 { x ( k ) } \{x^{(k)}\} {x(k)} 的 r r r 阶以 C C C 为因子收敛于 x ∗ x^* x∗
线性收敛
- 定义: r = 1 , 0 < C < 1 r=1,0 < C<1 r=1,0<C<1
- 性质: C C C 越小,算法收敛越快
超线性收敛
定义: r = 1 , C = 0 r=1,C=0 r=1,C=0
定理: r > 1 r>1 r>1 时的算法均为超线性收敛算法
{% fold light @证明 %}

{% endfold %}
1.4.4 迭代的终止条件
对于收敛速度比较慢的算法:
根据一阶必要条件,我们知道最优解一定取在微分算子为 0 的向量上,因此我们以下式为终止条件是一种可行的选择
∣ ∣ ∇ f ( x ( k ) ∣ ∣ ≤ ϵ ||\nabla f(x^{(k)}|| \le \epsilon ∣∣∇f(x(k)∣∣≤ϵ
但是问题在于这对收敛速度很快的算法不使用,如下图的无约束最优化问题。已知两个局部最优解分别为 x 1 ∗ , x 2 ∗ x_1^*,x_2^* x1∗,x2∗,迭代的两个解分别为 x ‾ 1 , x ‾ 2 \overline{x}_1,\overline{x}_2 x1,x2,可以看出:尽管 2 号点相对于 1 号点更靠近局部最优解,但是由于 2 号点的梯度更大,明显不如 1 号点更加局部最优,因此利用微分算子作为迭代的终止条件不适用于收敛速度快的算法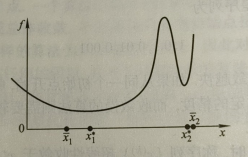
对于超线性收敛的算法:
一个理想的收敛终止条件为 ∣ ∣ x ( k ) − x ∗ ∣ ∣ ≤ ϵ ||x^{(k)} - x^*|| \le \epsilon ∣∣x(k)−x∗∣∣≤ϵ,但是由于最优解 x ∗ x^* x∗ 是未知的,因此该方案不可行,同理 f ( x ∗ ) f(x^*) f(x∗) 也是未知的,因此 ∣ ∣ f ( x ( k ) ) − f ( x ∗ ) ∣ ∣ ≤ ϵ ||f(x^{(k)}) - f(x^*)|| \le \epsilon ∣∣f(x(k))−f(x∗)∣∣≤ϵ 也是不可行的。那么有没有什么替代的方案呢?答案是有的。
方案一:利用函数解序列进行替代。即以下式作为迭代的终止条件
∣ ∣ x ( k + 1 ) − x ( k ) ∣ ∣ ≤ ϵ || x^{(k+1)} - x^{(k)} || \le \epsilon ∣∣x(k+1)−x(k)∣∣≤ϵ{% fold light @证明 %}

{% endfold %}方案二:利用函数值序列进行替代。即以下式作为迭代的终止条件
∣ ∣ f ( x ( k + 1 ) ) − f ( x ( k ) ) ∣ ∣ ≤ ϵ || f(x^{(k+1)}) - f(x^{(k)}) || \le \epsilon ∣∣f(x(k+1))−f(x(k))∣∣≤ϵ{% fold light @证明 %}

{% endfold %}
一般情况下,对于上述超线性算法的判断收敛的方法,只用其中一种往往不适当。此时一般使用两种方法集成的思路进行判断。
1.4.5 修正量的确定
本书介绍的迭代修正值都是使得当前迭代后的值小于上一个状态的函数值,我们称这类使评价函数值下降的算法为单调下降算法。至于如何得出修正量,我们往往通过求解一个相对简单易于求解的最优化问题(通常成为子问题),来计算获得修正量。
第二章「约束最优化」线性规划
{% note light %}
目标函数和约束函数都是线性函数。
{% endnote %}
2.1 线性规划问题和基本性质
2.1.1 线性规划问题
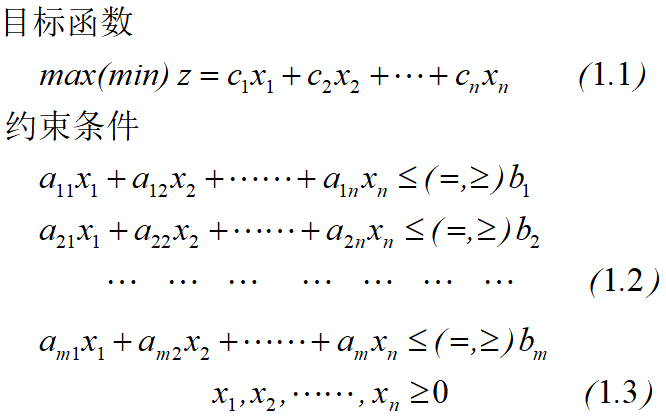
2.1.2 图解法
仅适用于二元变量的线性规划问题。我们将所有的约束条件全部画到平面直角坐标系中构成一个可行域,然后将目标函数作为一条直线进行平移,直到与可行域初次有交点,则该交点就是最优解对应的点。当然不一定会有交点,一共分为四种情况:
{% fold light @刚好只有一个最优解 %}
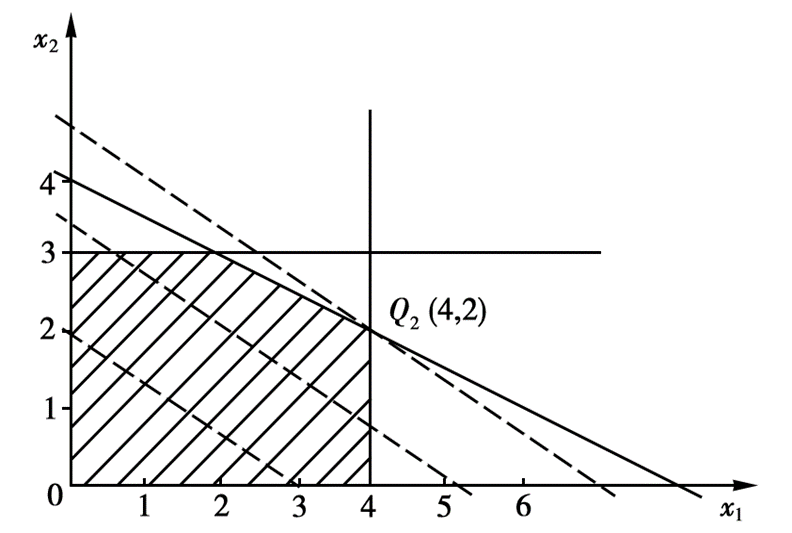
{% endfold %}
{% fold light @有无穷多最优解 %}
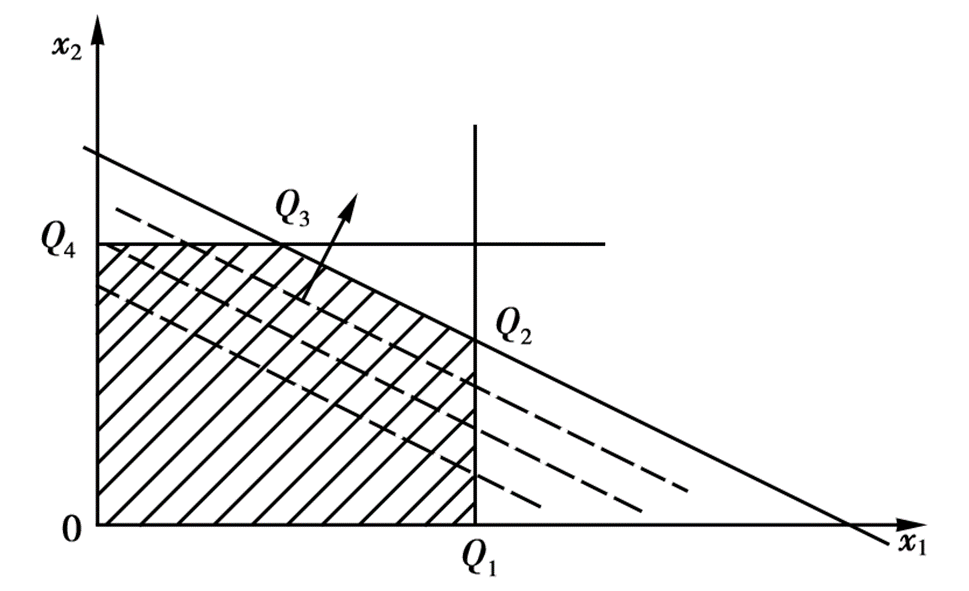
{% endfold %}
{% fold light @有无界解 %}
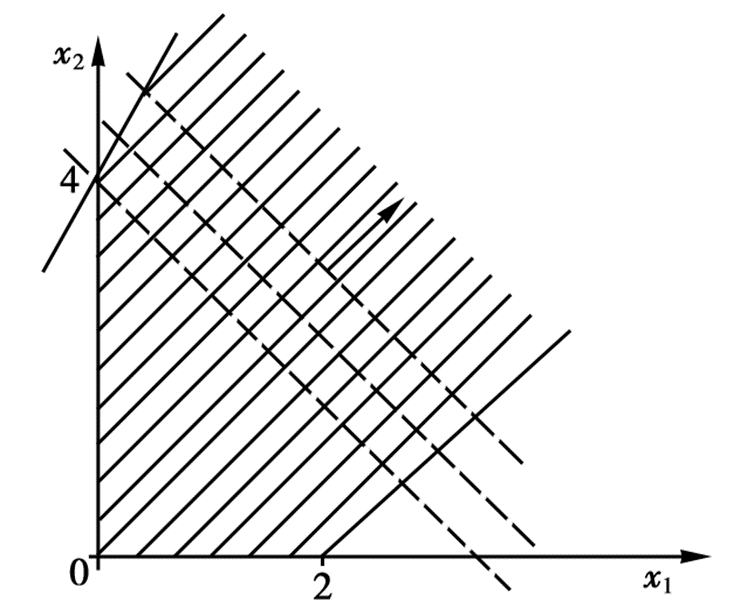
{% endfold %}
{% fold light @无可行解 - 可行域为空集 %}
{% endfold %}
2.1.3 基本性质
线性规划问题的可行域如果非空,则是一个凸集
{% fold light @证明 %}

{% endfold %}如果线性规划问题有最优解,那么最优解可在可行域的顶点中确定
如果可行域有界且可行域只有有限个顶点,则问题的最优解必存在,并在这有限个顶点中确定
最优解可由最优顶点处的有效约束形成的方程组的解确定
2.1.4 线性规划的标准形
为什么要学习线性规划的标准形?
- 我们要学习单纯形法来计算多维线性规划的最优解
- 单纯形法需要线性规划的具有所谓的标准形
线性规划的标准形的定义:
- 只含有线性等式约束和对变量的非负约束
一般线性规划转化为标准形的方法:
- 对于目标函数:需要将取 max \max max 通过取相反数转化为取 min \min min
- 对于约束条件:需要将不等式约束松弛转化为等式约束
- 对于 ≤ \le ≤ 的不等式约束,等式左边加上非负新变量,从而转化为等式
- 对于 ≥ \ge ≥ 的不等式约数,等式左边减去非负新变量,从而转化为等式
- 对于无约束的变量:需要将其转化为两个新变量之差(可正可负),产生了一个新的等式,如果该无约束变量存在于目标函数中,还需要将目标函数中的该变量表示为两个新变量之差
{% fold light @举个例子 %}

{% endfold %}
2.1.5 基本可行解
直接说结论:对于标准形的线性规划问题,其基本可行解就是凸集的顶点。
假设系数矩阵 A m , n A_{m, n} Am,n。基本可行解 ⊂ \subset ⊂ 基本解,而基本解的个数 ≤ C n m \le C_{n}^{m} ≤Cnm(因为分块矩阵 B m × m B_{m \times m} Bm×m 不一定可逆)。其中基本可行解需要满足解序列元素非负。如果基本变量向量对应的解中含有 0 元素,称其为退化的基本可行解,产生退化的基本可行解的原因是存在可删除的约数条件。
2.1.6 最优解的性质
若可行域有界,则线性规划问题的目标函数一定可以在其可行域的顶点上达到最优。
{% fold light @证明 - 反证法 %}

{% endfold %}有时,目标函数可能在多个顶点处达到最大,这时在这些顶点的凸组合上也达到最大值,这时线性规划问题有无限多个最优解。
2.2 单纯形法
{% note light %}
本目主要介绍一种常用的计算线性规划问题可行解的方法:单纯形法。其中,前三条分别介绍单纯性方法计算步骤的理论可行性,第四条具体介绍单纯形法的计算步骤与过程。
{% endnote %}
2.2.1 初始基可行解的确定
- 直接观察:直接看出系数矩阵中含有 m × m m \times m m×m 的单位矩阵,则选择该单位矩阵为初始基
- 加松弛变量:当所有的约束条件都是 ≤ \le ≤ 时,每一个约束条件都加一个非负的松弛变量,则这 m m m 个松弛变量的系数就对应了一个 m × m m \times m m×m 的单位矩阵,选择其为初始基即可
- 加非负的人工变量:求解方法与常规的线性规划问题不一样,见下述 2.2.3 条。
- 对于 = = = 约束,我们在约束条件的左边加上非负人工变量
- 对于 ≥ \ge ≥ 约束,我们先在约束条件的左边减去非负松弛变量,再在约束条件的左边加上非负的人工变量
2.2.2 最优性检验
{% fold light @符号说明 %}
一、当前局面:已经计算出一个基本可行解
1.1 确定线性规划的目标
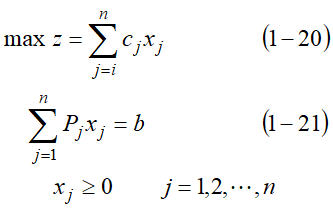
1.2 添加松弛变量

1.3 用非基变量线性表示基变量
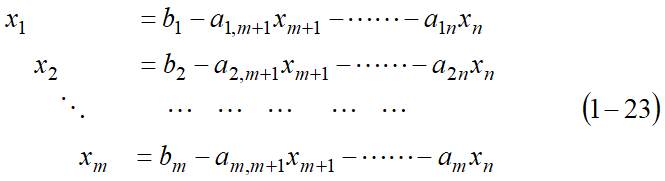
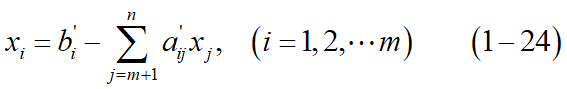
二、最优性检验

{% endfold %}
唯一最优解判别定理:对于目标函数求解最大值的情形。若 ∀ j ∈ [ m + 1 , n ] \forall j \in [m+1, n] ∀j∈[m+1,n] 有 σ j ≤ 0 \sigma_j \le 0 σj≤0 则当前基本可行解 x ( k ) x^{(k)} x(k) 为最优解。
无穷多最优解判别定理:在满足第一条所有的检验数非正的情况下, ∃ j ∈ [ m + 1 , n ] \exist j \in [m+1, n] ∃j∈[m+1,n],有 σ j = 0 \sigma_j=0 σj=0,则该线性规划问题有无穷多最优解。
{% fold light @证明 %}
我们可以将任意一个检验数为 0 的非基变量与基变量进行置换得到新的一个基本可行解对应的目标函数值保持不变。于是下述凸组合内的可行解都是最优解
x ( k ) s . t . { k ∈ [ m + 1 , n ] σ k = 0 \begin{aligned} & x^{(k)} \\ & s.t. \begin{cases} k &\in& [m+1, n] \\ \sigma_k &=& 0 \end{cases} \end{aligned} x(k)s.t.{kσk∈=[m+1,n]0
{% endfold %}无界解判别定理:pass
无解判别定理:可行域为空集
2.2.3 计算新的基本可行解
对于常规的线性规划问题(初始基本可行解 x ( 0 ) x^{(0)} x(0) 可以直接找到)
- 向量方程法
- 确定入基变量:选择目标函数中系数最大的变量作为入基变量,即将其对应的系数列向量与出基变量对应的系数列向量进行置换
- 确定出基变量:线性表示基方程组以后,利用变量非负的特性找到入基变量刚好取 0 0 0 时对应的变量即为出基变量(示例的第二轮迭代中出基变量即为 x 5 x_5 x5)
- 系数矩阵法
- pass
对于添加人工变量的线性规划问题(初始基本可行解 x ( 0 ) x^{(0)} x(0) 不能直接找到,需要手动构造 x ( 0 ) x^{(0)} x(0))
- 大 M 法:pass
- 两阶段法
- 第一阶段:pass
- 第二阶段:pass
2.2.4 单纯形表法
向量方程法:
{% fold light @实战演练 %}


{% endfold %}
单纯形表法:
{% fold light @实战演练 %}


{% endfold %}
2.3 对偶与对偶单纯形法
2.3.1 确定对偶问题
已知原问题的表达式,如何求解对偶问题的表达式?我们需掌握以下对偶转换规则:
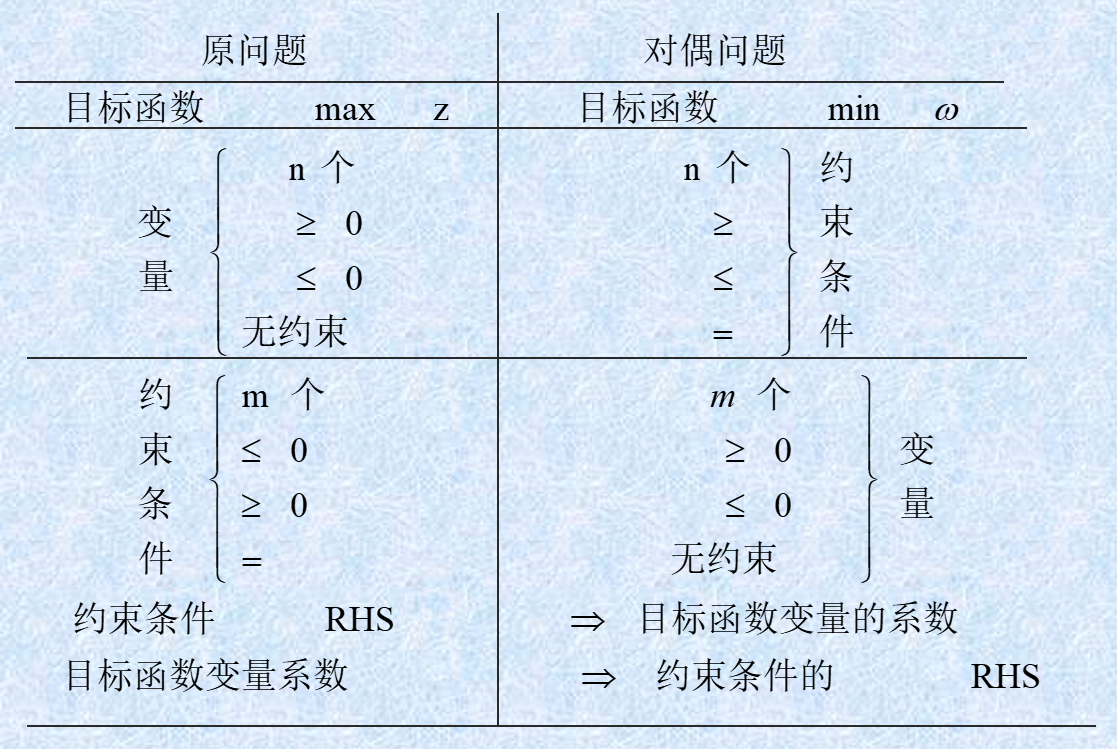
从上图不难发现,其实就是对线性规划的三个部分进行转换:目标函数、m个约束条件、n个自变量,下面分别进行文字介绍:
- 约束条件:从 m 个变为 n 个
- 常量矩阵中的元素为原问题中自变量的系数
- 二元关系的变化取决于转化方向
- max to min:对偶问题约束条件的符号和原问题自变量的符号相同
- min to max:对偶问题约束条件的符号和原问题自变量的符号相反
- 线性约束为原问题线性约束的转置
- 自变量:从 n 个变为 m 个
- 二元关系的变化同样取决于转化方向
- max to min:对偶问题自变量的符号和原问题约束条件的符号相反
- min to max:对偶问题自变量的符号和原问题约束条件的符号相同
- 二元关系的变化同样取决于转化方向
- 目标函数:自元个数从 n 个变为 m 个
- 变元的系数就是原问题中约束条件的常量矩阵对应的元素值
{% fold light @实战演练 %}
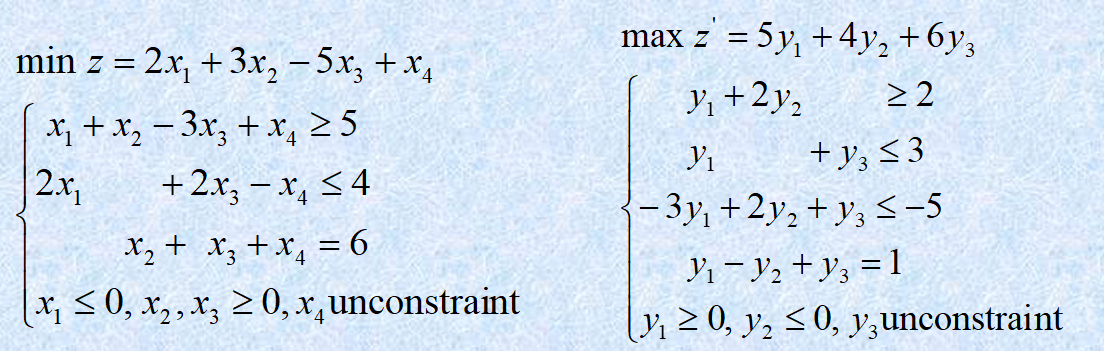
{% endfold %}
2.3.2 对偶定理
- 对称性:对偶问题的对偶问题是原问题
- 无界性:若原问题是无界解,则对偶问题无可行解
- 对偶定理:若原问题有最优解,那么对偶问题也有最优解,且目标函数值相等
- 互补松弛性:若原问题最优解为 x ∗ x^* x∗,对偶问题的最优解为 y ∗ y^* y∗,则有 x ∗ y s = 0 , y ∗ x s = 0 x^* y_s=0,y^*x_s=0 x∗ys=0,y∗xs=0,其中 x s , y s x_s,y_s xs,ys 分别为原问题的松弛变量和对偶问题的松弛变量
{% fold light @实战演练 %}

对于上述问题,我们可以先写出其对偶问题:
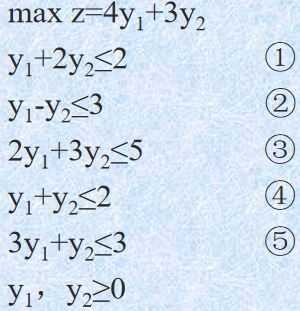
显然的对于 y ∗ = ( 4 5 , 3 5 ) T y^*=(\frac{4}{5},\frac{3}{5})^T y∗=(54,53)T,上述 2,3,4 是取不到等号的,对应的 x ∗ = ( − , 0 , 0 , 0 , − ) T x^*=(-,0,0,0,-)^T x∗=(−,0,0,0,−)T。还剩两个变量 x 1 , x 5 x_1,x_5 x1,x5 通过 1,5 两个不等式取等进行计算:
x 1 + 3 x 2 = 4 2 x 1 + x 2 = 3 \begin{aligned} x_1+3x_2=4\\ 2x_1+x_2=3 \end{aligned} x1+3x2=42x1+x2=3
计算可得 x 1 = 1 , x 5 = 1 x_1=1,x_5=1 x1=1,x5=1,于是原问题的最优解 x ∗ = ( 1 , 0 , 0 , 0 , 1 ) T x^*=(1, 0, 0, 0, 1)^T x∗=(1,0,0,0,1)T
{% endfold %}
2.3.3 对偶单纯形法
{% fold light @实战演练 %}


{% endfold %}
第三章 线性搜索
{% note light %}
本章介绍最优化问题中迭代解 x k + 1 = x k + α k d k x_{k+1} = x_k + \alpha_kd_k xk+1=xk+αkdk 基于「线性搜索」的迭代方式。
假设搜索方向 d k d_{k} dk 是一个定值且一定是下降方向,我们讨论步长因子 α k \alpha_{k} αk 的计算选择策略。分为两步:
- 确定步长的搜索区间
- 通过精确 or 不精确算法来搜索合适的步长
本章的内容分布:
- 3.1 介绍确定初始搜索区间的「进退法」
- 3.2 介绍缩小搜索区间的「精确线性搜索算法」:0.618 法、斐波那契法、二分法、插值法
- 3.3 介绍缩小搜索区间的「不精确线性搜索算法」:Armijo 准则、Goldstein 准则、Wolfe 准则
{% endnote %}
3.1 确定初始搜索区间
确定初始搜索区间 [ a , b ] [a,b] [a,b],我们利用 进退法
3.2 精确线性搜索算法
{% fold light @预备知识:单峰函数定理 %}
在正式开始介绍之前,我们先了解单峰函数定理:
定理:对于在区间 [ a , b ] [a,b] [a,b] 上的一个单峰函数 f ( x ) f(x) f(x), x ∗ ∈ [ a , b ] x^* \in [a,b] x∗∈[a,b] 是其极小点, x 1 x_1 x1 和 x 2 x_2 x2 是 [ a , b ] [a,b] [a,b] 上的任意两点,且 a < x 1 < x 2 < b a<x_1<x_2<b a<x1<x2<b,可以通过比较 f ( x 1 ) , f ( x 2 ) f(x_1),f(x_2) f(x1),f(x2) 的值来确定点的保留和舍弃
迭代:
若 f ( x 1 ) ≥ f ( x 2 ) f(x_1) \ge f(x_2) f(x1)≥f(x2) 则 x ∗ ∈ [ x 1 , b ] x^* \in [x_1,b] x∗∈[x1,b]
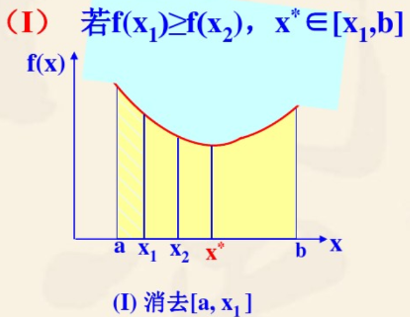
若 f ( x 1 ) < f ( x 2 ) f(x_1) < f(x_2) f(x1)<f(x2) 则 x ∗ ∈ [ a , x 2 ] x^* \in [a,x_2] x∗∈[a,x2]
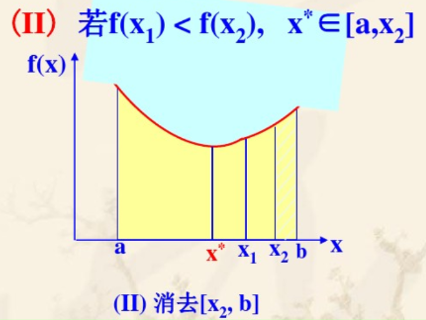
若 f ( x 1 ) = f ( x 2 ) f(x_1) = f(x_2) f(x1)=f(x2) 则 x ∗ ∈ [ x 1 , x 2 ] x^* \in [x_1,x_2] x∗∈[x1,x2]
于是迭代的关键就在于如何取点 x 1 x_1 x1 和 x 2 x_2 x2,下面开始介绍三种取点方法。
{% endfold %}
{% fold light @计算代码:基于 python 实现 0.618 法、斐波那契法、二分法 %}
迭代计算代码:
class ExactLinearSearch:
def __init__(self,
a: float, b: float, delta: float,
f: Callable[[float], float],
criterion: str="0.618", max_iter=100) -> None:
self.a = a
self.b = b
self.delta = delta
self.f = f
self.max_iter = max_iter
if criterion == "0.618":
new_a, new_b, x_star, count = self._f_goad()
elif criterion == "fibonacci":
new_a, new_b, x_star, count = self._f_fibo()
else: # criterion == "binary"
new_a, new_b, x_star, count = self._f_binary()
fixed = lambda x, acc: round(x, acc)
print(f"算法为:“{criterion}” 法")
print(f"共迭代:{count} 次")
print(f"左边界: {fixed(new_a, 4)}")
print(f"右边界: {fixed(new_b, 4)}")
print(f"最优解: {fixed(x_star, 4)}")
print(f"最优值: {fixed(f(x_star), 6)}\n")
def _f_goad(self) -> Tuple[float, float, float, int]:
a, b, delta, f = self.a, self.b, self.delta, self.f
count = 0
lam = a + 0.382 * (b - a)
mu = b - 0.382 * (b - a)
while count <= self.max_iter:
phi_lam = f(lam)
phi_mu = f(mu)
if phi_lam <= phi_mu:
b = mu
else:
a = lam
lam = a + 0.382 * (b - a)
mu = b - 0.382 * (b - a)
if b - lam <= delta:
return a, b, lam, count
if mu - a <= delta:
return a, b, mu, count
count += 1
return a, b, lam if f(lam) <= f(mu) else mu, count
def _f_fibo(self) -> Tuple[float, float, float, int]:
a, b, delta, f, max_iter = self.a, self.b, self.delta, self.f, self.max_iter
count = None
F = [0.0] * max_iter
F[1] = F[2] = 1
for i in range(3, max_iter):
F[i] = F[i - 1] + F[i - 2]
if F[i] >= (b - a) / delta:
count = i - 2
break
if count == None:
ValueError("区间过大或精度过高导致,找不到合适的迭代次数")
lam, mu = a, b
for i in range(3, count + 1):
lam = a + (1 - F[i - 1] / F[i]) * (b - a)
mu = b - (1 - F[i - 1] / F[i]) * (b - a)
if f(lam) <= f(mu):
b = mu
else:
a = lam
return a, b, lam if f(lam) <= f(mu) else mu, count
def _f_binary(self) -> Tuple[float, float, float, int]:
a, b, delta, f, max_iter = self.a, self.b, self.delta, self.f, self.max_iter
count = None
count = np.ceil(np.log2((b - a) / delta)).astype(int)
if count > max_iter:
ValueError("区间过大或精度过高导致迭代次数过高")
for _ in range(count):
c = (a + b) / 2.0
if f(c) >= 0.0:
b = c
else:
a = c
return a, b, c, count
分别调用 0.618 法、斐波那契法、二分法进行迭代计算:
a, b, delta = -1, 1, 0.01
f = lambda x: np.exp(-x) + np.exp(x) # 原函数
calc_goad = ExactLinearSearch(a, b, delta, f, criterion="0.618")
calc_fibo = ExactLinearSearch(a, b, delta, f, criterion="fibonacci")
a, b, delta = -3, 6, 0.1
f = lambda x: 2 * x + 2 # 导函数
calc_bina = ExactLinearSearch(a, b, delta, f, criterion="binary")
计算结果为:
算法为:“0.618” 法
共迭代:10 次
左边界: -0.0031
右边界: 0.0069
最优解: 0.0007
最优值: 2.000001
算法为:“fibonacci” 法
共迭代:11 次
左边界: -0.0225
右边界: 0.0
最优解: -0.0139
最优值: 2.000193
算法为:“binary” 法
共迭代:7 次
左边界: -1.0312
右边界: -0.9609
最优解: -0.9609
最优值: 0.078125
{% endfold %}
3.2.1 0.618 法
基于「函数值」进行选点。
按照黄金分割的比例取点 x 1 x_1 x1 和 x 2 x_2 x2,不断迭代判断 f ( x 1 ) f(x_1) f(x1) 和 f ( x 2 ) f(x_2) f(x2) 的值,直到 b k − λ k < δ b_k-\lambda_k<\delta bk−λk<δ 或 μ k − a k < δ \mu_k-a_k<\delta μk−ak<δ 则结束迭代,取最优解 x ∗ x^* x∗ 为对应的 λ k \lambda_k λk 或 μ k \mu_k μk 即可。
3.2.2 Fibonacci 法
基于「函数值」进行选点。
第 k k k 次迭代的区间长度是上一个区间长度的 F n − k F n − k + 1 \frac{F_{n-k}}{F_{n-k+1}} Fn−k+1Fn−k,即:
b k + 1 − a k + 1 = F n − k F n − k + 1 ( b k − a k ) b_{k+1} - a_{k+1} = \frac{F_{n-k}}{F_{n-k+1}} (b_{k} - a_{k}) bk+1−ak+1=Fn−k+1Fn−k(bk−ak)
经过 n n n 次迭代后,得到区间 [ a n , b n ] [a_n,b_n] [an,bn],且 b n − a n ≤ δ b_n-a_n \le \delta bn−an≤δ,于是可得:
b n − a n = F 1 F 2 ( b n − 1 − a n − 1 ) = F 1 F 2 F 2 F 3 ( b n − 2 − a n − 2 ) = ⋯ = F 1 F 2 F 2 F 3 ⋯ F n − 1 F n ( b 1 − a 1 ) = F 1 F n ( b 1 − a 1 ) ≤ δ \begin{aligned} b_n-a_n &= \frac{F_1}{F_2}(b_{n-1}-a_{n-1}) \\ &= \frac{F_1}{F_2} \frac{F_2}{F_3}(b_{n-2}-a_{n-2}) \\ &= \cdots \\ &= \frac{F_1}{F_2} \frac{F_2}{F_3} \cdots \frac{F_{n-1}}{F_n}(b_{1}-a_{1}) \\ &= \frac{F_1}{F_n}(b_1-a_1) \le \delta \end{aligned} bn−an=F2F1(bn−1−an−1)=F2F1F3F2(bn−2−an−2)=⋯=F2F1F3F2⋯FnFn−1(b1−a1)=FnF1(b1−a1)≤δ
在已知上界 δ \delta δ 的情况下可以直接计算出 n n n 的值,于是迭代 n n n 次即可得到最终的步长值 λ n \lambda_n λn 或 μ n \mu_n μn
3.2.3 二分法
基于「一阶导数」进行选点。
单调性存在于导数上。极值点左边导数 < 0 <0 <0,极值点右边导数 > 0 >0 >0,于是可以进行二分搜索。
3.2.4 插值法
基于「函数值、一阶导数」进行选点。
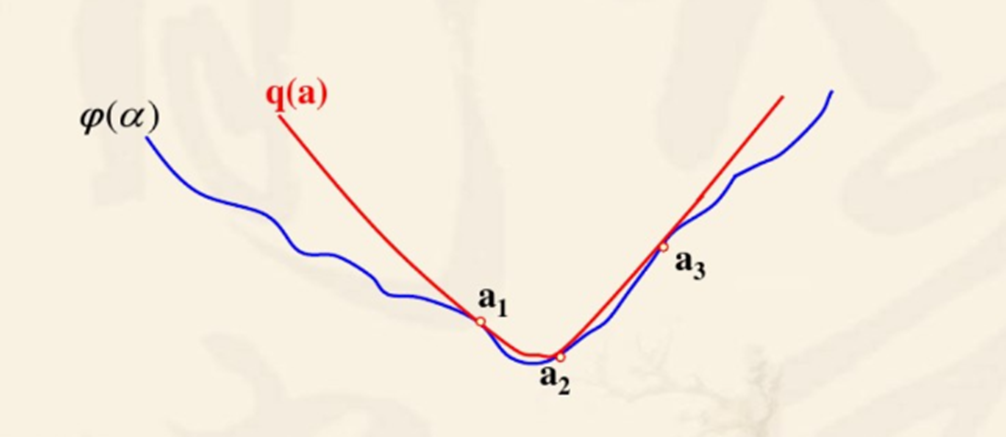
三点二次插值法。给定初始迭代区间 [ a 0 , b 0 ] [a_0,b_0] [a0,b0] 和初始迭代解 t 0 t_0 t0。每次在目标函数上取三个点来拟合一个二次函数,通过拟合出来的二次函数的最小值,来更新三个点为 a 1 , b 1 , t 1 a_1,b_1,t_1 a1,b1,t1,直到区间小于上界长度 δ \delta δ,终止迭代,极小值就是当前状态二次函数的最小值。
那么我们如何求解当前状态二次函数的最小值呢?假定三个已知点为 x 1 < x 2 < x 3 x_1<x_2<x_3 x1<x2<x3,且 f ( x 1 ) > f ( x 2 ) < f ( x 3 ) f(x_1)>f(x_2)<f(x_3) f(x1)>f(x2)<f(x3),我们需要知道二次函数的三个参数 a , b , c a,b,c a,b,c,刚好三个已知点可以得到三个方程,从而解出二次函数的三个未知数。
两点二次插值法。只不过少取了一个点,多利用了一个点的导数值来确定二次函数的三个参数罢了,其余迭代过程与三点二次插值完全一致。
3.3 不精确线性搜索算法
{% note light %}
精确搜索有时会导致搜索时间过长,尤其是当最优解离当前点还很远时。接下来我们介绍不精确线性搜索方法,在确保每一步的函数值都有充分下降的必要条件下,确保收敛并提升计算效率。真的有这么厉害的算法吗?其实根本逻辑很简单,Armijo 准则限定了搜索方向的上界、Goldstein 准则在前者的基础上又限定了搜索方向的下界(防止过小导致收敛过慢)、Wolfe 准则在前者的基础上又完善了下界的约束(确保不会把可行解排除在搜索区间外)
{% endnote %}
符号定义:我们在已知上一步解 x k x_k xk 和下次迭代的下降方向 d k d_k dk 的基础上,需要寻找合适的 α \alpha α。于是唯一变量就是 α \alpha α,我们直接定义关于 α \alpha α 的一元函数 ϕ ( α ) = f ( x k + α d k ) \phi(\alpha) = f(x_k + \alpha d_k) ϕ(α)=f(xk+αdk), g k g_k gk 表示梯度。
3.3.1 Armijo 准则
只限定搜索上界,给定初始点 x 0 x_0 x0、系数 ρ \rho ρ:
f ( x k + α d k ) ≤ ρ ⋅ g k T d k ⋅ α + f ( x k ) f(x_k + \alpha d_k) \le \rho \cdot g_k^Td_k \cdot \alpha + f(x_k) f(xk+αdk)≤ρ⋅gkTdk⋅α+f(xk)
3.3.2 Goldstein 准则
又限定了搜索下界,同样给定初始点 x 0 x_0 x0、系数 ρ \rho ρ:
f ( x k + α d k ) ≤ ρ ⋅ g k T d k ⋅ α + f ( x k ) f ( x k + α d k ) ≥ ( 1 − ρ ) ⋅ g k T d k ⋅ α + f ( x k ) \begin{aligned} f(x_k + \alpha d_k) \le &\rho \cdot g_k^Td_k \cdot \alpha + f(x_k)\\ f(x_k + \alpha d_k) \ge &(1-\rho) \cdot g_k^Td_k \cdot \alpha + f(x_k) \end{aligned} f(xk+αdk)≤f(xk+αdk)≥ρ⋅gkTdk⋅α+f(xk)(1−ρ)⋅gkTdk⋅α+f(xk)
3.3.3 Wolfe 准则
完善了搜索下界的约束,即保证新点的梯度 g k + 1 T d k g_{k+1}^Td_k gk+1Tdk 不低于老点梯度 g k T d k g_{k}^Td_k gkTdk 的 σ \sigma σ 倍。给定 x 0 , ρ , σ x_0,\rho,\sigma x0,ρ,σ:
f ( x k + α d k ) ≤ ρ ⋅ g k T d k ⋅ α + f ( x k ) g ( x k + α k d k ) T d k ≥ σ g k T d k 0 < ρ < σ < 1 \begin{aligned} f(x_k + \alpha d_k) \le &\rho \cdot g_k^Td_k \cdot \alpha + f(x_k)\\ g(x_k + \alpha_kd_k)^Td_k \ge& \sigma g_{k}^Td_k\\ 0 < \rho < \sigma < 1 \end{aligned} f(xk+αdk)≤g(xk+αkdk)Tdk≥0<ρ<σ<1ρ⋅gkTdk⋅α+f(xk)σgkTdk
参考:
第四章「无约束最优化」
{% note light %}
本章介绍无约束函数的最优化算法。其中:
- 最速下降法基于「一阶梯度」。最基本的方法
- 牛顿法基于「二阶梯度」。最主要的方法
- 共轭梯度法基于「一阶梯度」。解大型最优化问题的首选
- 拟牛顿法基于「函数值和一阶梯度」。尤其是其中的 BFGS 是目前最成功的方法
{% endnote %}
{% fold light @极小化 Rosenbrock 函数的 python 代码 %}
目标函数 f f f、一阶梯度 g g g、二阶梯度 G G G、初始点 x 0 x_0 x0
def f(x: np.ndarray) -> float:
return (1 - x[0])**2 + 100 * (x[1] - x[0]**2)**2
def g(x: np.ndarray) -> np.ndarray:
grad_x = -2 * (1 - x[0]) - 400 * x[0] * (x[1] - x[0]**2)
grad_y = 200 * (x[1] - x[0]**2)
return np.array([grad_x, grad_y])
def G(x: np.ndarray) -> np.ndarray:
grad_xx = 2 - 400 * x[1] + 1200 * x[0]**2
grad_xy = -400 * x[0]
grad_yx = -400 * x[0]
grad_yy = 200
return np.array([
[grad_xx, grad_xy],
[grad_yx, grad_yy]
])
initial_point = [-1.2, 1]
已知最优点为 x ∗ = ( 1 , 1 ) T x^*=(1, 1)^T x∗=(1,1)T,最优解 f ( x ∗ ) = 0 f(x^*)=0 f(x∗)=0,以书中例题初始点 ( − 1.2 , 1 ) T (-1.2,1)^T (−1.2,1)T 为例开始迭代。
一、最速下降法
def gradient_descent(initial_point, max_iter=5, eps=1e-6):
x = np.array(initial_point)
points = [x]
gradients = [g(x)]
alphas = []
for _ in range(max_iter):
grad = gradients[-1]
# 搜索方向
direction = -grad
# 步长因子:无法确定准确的步长最小化函数,因此此处采用二分法搜索最优步长
alpha = 1
while f(x + alpha * direction) > f(x):
alpha /= 2
x = x + alpha * direction
points.append(x)
gradients.append(g(x))
alphas.append(alpha)
if np.linalg.norm(grad) < eps:
break
return points, gradients, alphas
points, gradients, alphas = gradient_descent(initial_point, max_iter=100, eps=1e-6)
for i, (point, grad, alpha) in enumerate(zip(points, gradients, [1] + alphas)):
print(f"Iteration {i}:")
print(f" Point = {point}")
print(f" Gradient = {grad}")
print(f" Step Size = {alpha}")
print(f" Direction = {-grad}")
print(f" Function Val= {f(point)}\n")
迭代100次后输出为:
Iteration 98:
Point = [0.93432802 0.87236513]
Gradient = [ 0.0942865 -0.12074477]
Step Size = 0.00390625
Direction = [-0.0942865 0.12074477]
Function Val= 0.004349256784446673
Iteration 99:
Point = [0.93414387 0.87260096]
Gradient = [-0.12281587 -0.00476179]
Step Size = 0.001953125
Direction = [0.12281587 0.00476179]
Function Val= 0.004337086557103718
Iteration 100:
Point = [0.93438374 0.87261026]
Gradient = [ 0.04171114 -0.09254423]
Step Size = 0.001953125
Direction = [-0.04171114 0.09254423]
Function Val= 0.004326904052586884
二、牛顿法
def newton_method(initial_point, max_iter=5, eps=1e-6):
x = np.array(initial_point)
points = [x]
gradients = [g(x)]
Hessians = [G(x)]
for _ in range(max_iter):
grad = gradients[-1]
Hessian = Hessians[-1]
# 搜索方向
direction = np.linalg.inv(Hessian) @ grad
# 步长因子:假定使用固定步长的牛顿法
alpha = 1
x = x - alpha * direction
points.append(x)
gradients.append(g(x))
Hessians.append(G(x))
if np.linalg.norm(grad) < eps:
break
return points, gradients, Hessians
points, gradients, Hessians = newton_method(initial_point, max_iter=50, eps=1e-6)
for i, (point, grad, Hessian) in enumerate(zip(points, gradients, Hessians)):
print(f"Iteration {i}:")
print(f" Point = {point}")
print(f" Gradient = {grad}")
print(f" Hessian = {Hessian}")
print(f" Function Val= {f(point)}\n")
迭代7次即收敛:
Iteration 5:
Point = [0.9999957 0.99999139]
Gradient = [-8.60863343e-06 -2.95985458e-11]
Hessian = [[ 801.99311306 -399.99827826]
[-399.99827826 200. ]]
Function Val= 1.8527397192178054e-11
Iteration 6:
Point = [1. 1.]
Gradient = [ 7.41096051e-09 -3.70548037e-09]
Hessian = [[ 802.00000001 -400. ]
[-400. 200. ]]
Function Val= 3.4326461875363225e-20
Iteration 7:
Point = [1. 1.]
Gradient = [-0. 0.]
Hessian = [[ 802. -400.]
[-400. 200.]]
Function Val= 0.0
三、共轭梯度法
def conjugate_gradient(initial_point, max_iter=5, eps=1e-6):
x = np.array(initial_point)
points = [x]
gradients = [g(x)]
directions = [-g(x)]
alphas = []
for i in range(max_iter):
grad = gradients[-1]
# 搜索方向:FR公式
if i == 0:
direction = -grad
else:
beta = np.dot(g(x), g(x)) / np.dot(g(points[-2]), g(points[-2]))
direction = -g(x) + beta * direction
# 步长因子:精确线搜索直接得到闭式解
alpha = -np.dot(grad, direction) / np.dot(direction, G(x) @ direction)
x = x + alpha * direction
directions.append(direction)
alphas.append(alpha)
points.append(x)
gradients.append(g(x))
if np.linalg.norm(grad) < eps:
break
return points, gradients, alphas
points, gradients, alphas = conjugate_gradient(initial_point, max_iter=1000, eps=1e-6)
for i, (point, grad, alpha) in enumerate(zip(points, gradients, alphas)):
print(f"Iteration {i}:")
print(f" Point = {point}")
print(f" Gradient = {grad}")
print(f" Step Size = {alpha}")
print(f" Direction = {-grad}")
print(f" Function Val= {f(point)}\n")
迭代1000次后输出为:
Iteration 997:
Point = [0.9999994 0.99999875]
Gradient = [ 1.90794906e-05 -1.01414007e-05]
Step Size = 0.0005161468619784313
Direction = [-1.90794906e-05 1.01414007e-05]
Function Val= 6.191018745155016e-13
Iteration 998:
Point = [0.99999931 0.99999861]
Gradient = [ 5.43686111e-06 -3.40374227e-06]
Step Size = 0.0005078748917694624
Direction = [-5.43686111e-06 3.40374227e-06]
Function Val= 4.986125950068217e-13
Iteration 999:
Point = [0.9999993 0.9999986]
Gradient = [ 1.34784246e-06 -1.36924747e-06]
Step Size = 0.0005356250138048412
Direction = [-1.34784246e-06 1.36924747e-06]
Function Val= 4.881643528976312e-13
四、拟牛顿法
def bfgs(initial_point, max_iter=5, eps=1e-6):
x = np.array(initial_point)
points = [x]
gradients = [g(x)]
B = G(x)
for _ in range(max_iter):
grad = gradients[-1]
# 迭代公式
x = x - np.linalg.inv(B) @ grad
# 更新 B 矩阵
s = x - points[-1]
y = g(x) - gradients[-1]
B = B + np.outer(y, y) / (s @ y) - (B @ np.outer(s, s) @ B) / (s @ B @ s)
points.append(x)
gradients.append(g(x))
if np.linalg.norm(grad) < eps:
break
return points, gradients
points, gradients = bfgs(initial_point, max_iter=1000, eps=1e-6)
for i, (point, grad) in enumerate(zip(points, gradients)):
print(f"Iteration {i}:")
print(f" Point = {point}")
print(f" Gradient = {grad}")
print(f" Function Val= {f(point)}\n")
迭代 78 次收敛:
Iteration 76:
Point = [1.00000075 0.99999921]
Gradient = [ 0.000918 -0.00045825]
Function Val= 5.255482679080297e-10
Iteration 77:
Point = [1.00000006 1.00000012]
Gradient = [ 6.46055099e-07 -2.63592925e-07]
Function Val= 3.7061757712619374e-15
Iteration 78:
Point = [1. 1.]
Gradient = [6.75185684e-10 4.68913797e-10]
Function Val= 6.510026595267928e-19
{% endfold %}
4.1 最速下降法
放一张生动的图:

迭代公式:
x k + 1 = x k − α k ∇ f ( x k ) x_{k+1} = x_k - \alpha_k \nabla f(x_k) xk+1=xk−αk∇f(xk)
每次迭代时,下降方向 d k d_k dk 采用当前解 x k x_k xk 处的负梯度方向 − ∇ f ( x k ) - \nabla f(x_k) −∇f(xk),步长因子 α k \alpha_k αk 采用精确线性搜索算法的计算结果。
易证相邻迭代解 x k , x k + 1 x_k,x_{k+1} xk,xk+1 的方向 d k , d k + 1 d_k,d_{k+1} dk,dk+1 是正交的:由于 ϕ ( α ) = f ( x k + α d k ) \phi(\alpha) = f(x_k + \alpha d_k) ϕ(α)=f(xk+αdk),在采用线搜索找最优步长时,步长的搜索结果 α k \alpha_k αk 即为使得 ϕ ′ ( α ) = 0 \phi'(\alpha)=0 ϕ′(α)=0 的解,于是可得 0 = ϕ ′ ( α ) = ϕ ′ ( α k ) = ∇ f ( x k + α k d k ) d k = − d k + 1 T ⋅ d k 0=\phi'(\alpha) = \phi'(\alpha_k) = \nabla f(x_k+\alpha_k d_k)d_k = -d_{k+1}^T \cdot d_k 0=ϕ′(α)=ϕ′(αk)=∇f(xk+αkdk)dk=−dk+1T⋅dk,即 d k + 1 T ⋅ d k = 0 d_{k+1}^T \cdot d_k = 0 dk+1T⋅dk=0。如图:
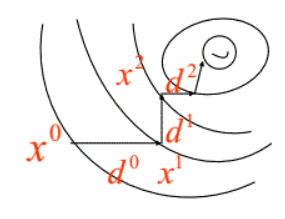
也正因为搜索方向正交的特性导致最速下降法的收敛速度往往不尽如人意。优点在于程序设计简单并且计算和存储量都不大,以及对初始点的要求不高。
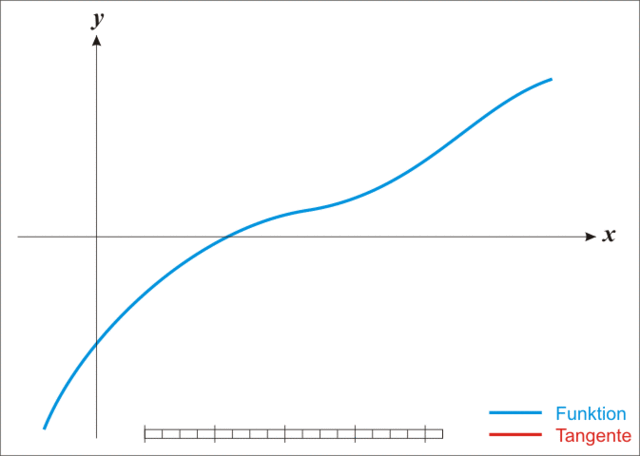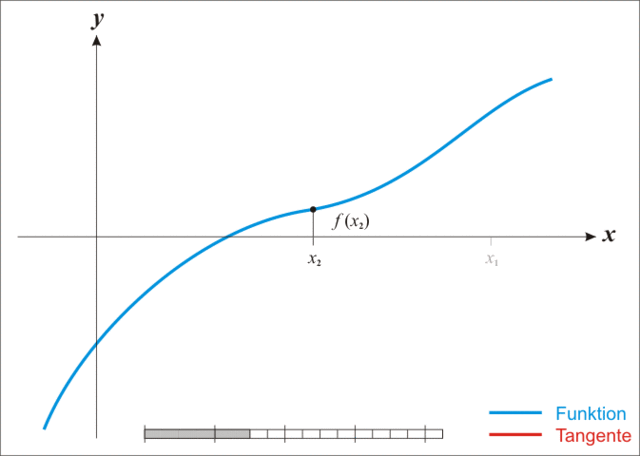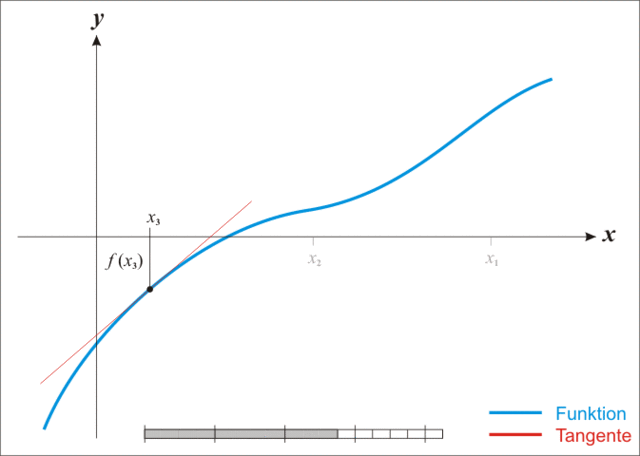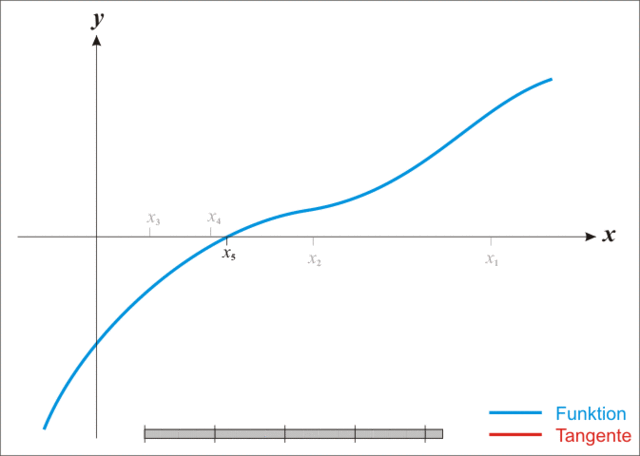
4.2 牛顿法
放一张生动的图:
{% note warning %}
注:本图演示的是求解一维函数零点的迭代过程,需要使得 f ( x ) = 0 f(x)=0 f(x)=0,因此比值式为原函数除以导函数。后续介绍的是极小化函数的过程,需要使得 f ′ ( x ) = 0 f'(x)=0 f′(x)=0,因此比值式为一阶导数除以二阶导数,高维就是二阶梯度的逆乘以一阶梯度。
{% endnote %}
迭代公式:
x k + 1 = x k − ∇ 2 f ( x k ) − 1 ∇ f ( x k ) x_{k+1} = x_k - \nabla^2f(x_k)^{-1}\nabla f(x_k) xk+1=xk−∇2f(xk)−1∇f(xk)
牛顿法相较于最速下降法有了更快的收敛速度,但是由于需要计算和存储海塞矩阵导致计算量增加并且有些目标函数可能根本求不出二阶梯度。同时牛顿法对于初始迭代点的选择比最速下降法要苛刻的多。
4.3 共轭梯度法
我们利用共轭梯度法解决「正定二次函数」的极小化问题。由于最速下降法中相邻迭代点的方向是正交的导致搜索效率下降,牛顿法又由于需要计算和存储海塞矩阵导致存储开销过大,共轭梯度法的核心思想是相邻两个迭代点的搜索方向是关于正定二次型的正定阵正交的。这样既保证了迭代收敛的速度也避免了计算存储海塞矩阵的开销。美中不足的是当共轭梯度法解决其他问题是往往会出现对线搜索的过度依赖,一旦线搜索变差会导致整个迭代过程精度变差。
概念补充:
- 共轭: x x x 与 y y y 共轭当且仅当 x T G y = 0 x^TGy=0 xTGy=0,其中 G 为对称正定阵
- 正定二次: f ( x ) = 1 2 x T G x − b T x + c f(x) =\frac{1}{2} x^TGx - b^Tx + c f(x)=21xTGx−bTx+c
公式推导:
首先给定初始迭代点 x 0 x_0 x0,收敛阈值 ϵ \epsilon ϵ,迭代公式是不变的: x k + 1 = x k + α k d k x_{k+1} = x_k + \alpha_k d_k xk+1=xk+αkdk,关键在于计算每一次迭代过程中的步长因子 α k \alpha_k αk 和搜索方向 d k d_k dk
确定步长因子 α k \alpha_k αk:
α = min α ϕ ( α ) = min α f ( x k + α d k ) = min α 1 2 ( x k + α d k ) T G ( x k + α d k ) − b T ( x k + α d k ) + c = min α 1 2 ( x k T G x k + 2 α x k T G d k + α 2 d K T d k ) − b T x k − b T α d k + c = min α 1 2 x k T G x k + α x k T G d k + 1 2 α 2 d k T G d k − b T α d k + c \begin{aligned} \alpha &= \min_{\alpha} \phi(\alpha) \\ &= \min_{\alpha} f(x_k+\alpha d_k) \\ &= \min_{\alpha} \frac{1}{2}(x_k+\alpha d_k)^TG(x_k+\alpha d_k) - b^T(x_k+\alpha d_k) + c \\ &= \min_{\alpha} \frac{1}{2} (x_k^TGx_k + 2\alpha x_k^T G d_k + \alpha^2d_K^Td_k) - b^Tx_k - b^T \alpha d_k + c\\ &= \min_{\alpha} \frac{1}{2} x_k^TGx_k + \alpha x_k^T G d_k + \frac{1}{2}\alpha^2d_k^T G d_k - b^T \alpha d_k + c \end{aligned} α=αminϕ(α)=αminf(xk+αdk)=αmin21(xk+αdk)TG(xk+αdk)−bT(xk+αdk)+c=αmin21(xkTGxk+2αxkTGdk+α2dKTdk)−bTxk−bTαdk+c=αmin21xkTGxk+αxkTGdk+21α2dkTGdk−bTαdk+c
由于目标函数是正定二次型,显然可以直接求出步长因子的闭式解:
d ϕ ( α ) d α = x k T G d k + α d k T G d k − b T d k = 0 \begin{aligned} \frac{d \phi(\alpha)}{d\alpha} &= x_k^T G d_k + \alpha d_k^T G d_k - b^Td_k \\ &=0 \end{aligned} dαdϕ(α)=xkTGdk+αdkTGdk−bTdk=0
于是可以导出当前的步长因子 α k \alpha_k αk 的闭式解为:
α k = ( b T − x T G ) d k d k T G d k = − g k T d k d k T G d k \begin{aligned} \alpha_k &= \frac{(b^T - x^TG)d_k}{d_k^TGd_k} \\ &= -\frac{g_k^T d_k}{d_k^TGd_k} \end{aligned} αk=dkTGdk(bT−xTG)dk=−dkTGdkgkTdk确定搜索方向 d k d_k dk:
d k = − g k + β d k − 1 d_k = -g_k + \beta d_{k-1} dk=−gk+βdk−1
可见只需要确定组合系数 β \beta β。由于共轭梯度法遵循相邻迭代点的搜索方向共轭,即 d k − 1 T G d k = 0 d_{k-1}^TGd_k=0 dk−1TGdk=0,因此对上式两侧同时左乘 d k − 1 T G d_{k-1}^TG dk−1TG,有:
d k − 1 T G d k = − d k − 1 T G g k + β d k − 1 T G d k − 1 = 0 \begin{aligned} d_{k-1}^TGd_k &= -d_{k-1}^TGg_k + \beta d_{k-1}^TGd_{k-1} \\ &= 0 \end{aligned} dk−1TGdk=−dk−1TGgk+βdk−1TGdk−1=0
于是可得当前的组合系数 β \beta β 为:
β = d k − 1 T G g k d k − 1 T G d k − 1 \beta = \frac{d_{k-1}^TGg_k}{d_{k-1}^TGd_{k-1}} β=dk−1TGdk−1dk−1TGgk
{% note warning %}上述组合系数 β \beta β 的结果是共轭梯度最原始的表达式,后人又进行了变形,
没证出来,难崩,直接背吧,给出 FR 的组合系数表达式:
β = g k T g k g k − 1 T g k − 1 \begin{aligned} \beta = \frac{g_k^Tg_k}{g_{k-1}^T g_{k-1}} \end{aligned} β=gk−1Tgk−1gkTgk
{% endnote %}当然了由于初始迭代时没有前一个搜索方向,因此直接用初始点的梯度作为搜索方向,即:
d 0 = − g 0 d_0=-g_0 d0=−g0
于是可以导出当前的搜索方向 d k d_k dk 的闭式解为:
d k = − g k + g k T g k g k − 1 T g k − 1 d k − 1 d_k = -g_k + \frac{g_k^Tg_k}{g_{k-1}^T g_{k-1}} d_{k-1} dk=−gk+gk−1Tgk−1gkTgkdk−1
迭代公式:
x k + 1 = x k + α k d k = x k + ( − g k T d k d k T G d k ) ( − g k + g k T g k g k − 1 T g k − 1 d k − 1 ) \begin{aligned} x_{k+1} =& x_k + \alpha_k d_k\\ =& x_k + (-\frac{g_k^T d_k}{d_k^TGd_k}) (-g_k + \frac{g_k^Tg_k}{g_{k-1}^T g_{k-1}} d_{k-1}) \end{aligned} xk+1==xk+αkdkxk+(−dkTGdkgkTdk)(−gk+gk−1Tgk−1gkTgkdk−1)
4.4 拟牛顿法
4.1 和 4.2 介绍的基于一阶梯度和二阶梯度的下降法都可以统一成下面的表达式:
x k + 1 = x k − α k B k ∇ f ( x k ) x_{k+1} = x_k - \alpha_k B_k \nabla f(x_k) xk+1=xk−αkBk∇f(xk)
- 4.1 的最速下降法的步长因子通过精确线搜索获得,海塞矩阵的逆 B k B_k Bk 不存在,可以看做为单位阵 E E E
- 4.2 的牛顿法的步长因子同样可以通过精确线搜索获得,当然也可以设置为定值,海塞矩阵的逆 B k B_k Bk 对应二阶梯度的逆 ( ∇ 2 f ( x k ) ) − 1 (\nabla^2 f(x_k))^{-1} (∇2f(xk))−1
前者收敛速度差、后者计算量和存储量大,我们尝试构造一个对称正定阵 B k B_k Bk 来近似代替二阶梯度的逆,即 B k ≈ ( ∇ 2 f ( x k ) ) − 1 B_k \approx (\nabla^2 f(x_k))^{-1} Bk≈(∇2f(xk))−1,使得该法具备较快的收敛速度与较少的内存开销。
介绍最著名的 BFGS 拟牛顿法,它的核心思想是每次迭代过程中对其进行快速校正,从而在确保收敛速度的情况下提升计算效率。迭代公式如下:
x k + 1 = x k − B k − 1 g k 记: { s k = x k + 1 − x k y k = g k + 1 − g k 则: { B 0 = ∇ 2 f ( x 0 ) B k + 1 = B k + y k y k T s k T y k − B k s k s k T B k s k T B k s k \begin{aligned} &x_{k+1} = x_k - B_k^{-1}g_k \\ &\text{记: } \begin{cases} s_k= x_{k+1} - x_k\\ y_k=g_{k+1} - g_k \end{cases}\\ &\text{则: } \begin{cases} B_0 = \nabla^2f(x_0)\\ \displaystyle B_{k+1} = B_k + \frac{y_ky_k^T}{s_k^Ty_k} - \frac{B_ks_ks_k^TB_k}{s_k^TB_ks_k} \end{cases} \end{aligned} xk+1=xk−Bk−1gk记: {sk=xk+1−xkyk=gk+1−gk则: ⎩
⎨
⎧B0=∇2f(x0)Bk+1=Bk+skTykykykT−skTBkskBkskskTBk
参考:
第五章「无约束最优化」最小二乘
{% note light %}
本章继续介绍无约束函数的最优化算法。不过和第四章的区别在于现在的目标函数是二次函数,称为「最小二乘问题」。
所谓的无约束最小二乘问题,本质上是第四章介绍的无约束问题的一个子集,只不过因为使用场景很多所以单独拿出来进行讨论。也正因为使用场景多,学者们针对此类问题设计出了更加高效的最优化算法。
无约束最小二乘问题的形式定义为:
min x ∈ R n f ( x ) = 1 2 ∑ i = 1 m [ r i ( x ) ] 2 , m ≥ n \begin{aligned} \min_{x\in R^n}f(x)=\frac{1}{2}\sum_{i=1}^m[r_{i}(x)]^2,\quad m\ge n \end{aligned} x∈Rnminf(x)=21i=1∑m[ri(x)]2,m≥n
其中 r i ( x ) r_i(x) ri(x) 称为「残量函数」。本质上最小二乘问题就是寻找一个函数 f ( x , α i ) , ( i = 1 , 2 , ⋯ , m ) f(x,\alpha_i),(i=1,2,\cdots,m) f(x,αi),(i=1,2,⋯,m) 来拟合 b b b,于是问题就转化为了
min ∑ i = 1 m [ r i ( x ) ] 2 = min ∑ i = 1 m [ f ( x , α i ) − b i ] 2 \begin{aligned} \min { \sum_{i=1}^m [r_i(x)]^2 }=\min { \sum_{i=1}^m [f(x,\alpha_i) - b_i]^2 } \end{aligned} mini=1∑m[ri(x)]2=mini=1∑m[f(x,αi)−bi]2
当 r i ( x ) r_i(x) ri(x) 为线性函数时,当前问题为线性最小二乘问题;当 r i ( x ) r_i(x) ri(x) 为非线性函数时,当前问题为非线性最小二乘问题。本章将分别讨论这两种最小二乘问题的优化求解策略。
{% endnote %}
5.1 线性最小二乘
此时可以直接将目标函数写成:
min f ( x ) = 1 2 ∣ ∣ A x − b ∣ ∣ 2 = 1 2 x T A T A x − b T A x + 1 2 b T b \begin{aligned} \min f(x)&=\frac{1}{2}|| Ax-b ||^2\\ &= \frac{1}{2}x^TA^TAx-b^TAx+\frac{1}{2}b^Tb \end{aligned} minf(x)=21∣∣Ax−b∣∣2=21xTATAx−bTAx+21bTb
利用一阶必要条件可得:
∇ f ( x ) = A T A x − A T b = 0 \begin{aligned} \nabla f(x)&=A^TAx - A^Tb\\ &=0 \end{aligned} ∇f(x)=ATAx−ATb=0
于是可得最优闭式解:
x ∗ = ( A T A ) − 1 A T b x^*=(A^T A)^{-1}A^Tb x∗=(ATA)−1ATb
当然 A T A A^TA ATA 并不都是可逆的,并且在数据量足够大时,即使可逆也会让求逆操作即为耗时。针对此问题,提出了线性最小二乘的 QR 正交分解算法。
5.2 非线性最小二乘
同样可以采用第四章学到的各种下降迭代算法,这里引入高斯牛顿法,推导的解的迭代公式为:
x k + 1 = x k − ( A k T A k ) − 1 A k T r k x^{k+1}=x^k - (A_k^TA_k)^{-1}A_k^Tr_k xk+1=xk−(AkTAk)−1AkTrk
其中:
A k = [ ∇ r 1 ( x k ) ∇ r 2 ( x k ) ⋮ ∇ r m ( x k ) ] , r k = [ r 1 ( x k ) r 2 ( x k ) ⋮ r m ( x k ) ] \begin{aligned} A_k = \begin{bmatrix} \nabla r_1(x_k)\\ \nabla r_2(x_k)\\ \vdots \\ \nabla r_m(x_k) \end{bmatrix},\quad r_k = \begin{bmatrix} r_1(x_k)\\ r_2(x_k)\\ \vdots \\ r_m(x_k) \end{bmatrix}\\ \end{aligned} Ak=
∇r1(xk)∇r2(xk)⋮∇rm(xk)
,rk=
r1(xk)r2(xk)⋮rm(xk)
参考:
第六章「约束最优化」二次规划
{% note light %}
目标函数是二次函数,约束函数是线性函数。一般形式为:
min q ( x ) = 1 2 x T G x + g T x s . t . { a i T x = b i , i ∈ S a i T x ≥ b i , i ∈ M \begin{aligned} &\min \quad q(x) = \frac{1}{2}x^TGx + g^Tx \\ &s.t.\quad \begin{cases} a_i^Tx = b_i& ,i\in S\\ a_i^Tx \ge b_i& ,i \in M\\ \end{cases} \end{aligned} minq(x)=21xTGx+gTxs.t.{aiTx=biaiTx≥bi,i∈S,i∈M
本章将分别讨论约束函数「含有等式」和「含有不等式」两类二次规划问题。
{% endnote %}
6.1 等式约束二次规划
我们引入拉格朗日方法 (Lagrange Method, 简称 LM)。此时可以用矩阵表示问题和约束条件,并且不加证明的给出最优解和对应乘子就是满足 KKT 条件下的解。
拉格朗日函数:
L ( x , λ ) = 1 2 x T G x + g T x − λ T ( A T x − b ) L(x,\lambda) = \frac{1}{2}x^TGx+g^Tx -\lambda^T(A^Tx - b) L(x,λ)=21xTGx+gTx−λT(ATx−b)
一阶必要条件:
∂ L ( x , λ ) ∂ x = G x + g − A λ = 0 ∂ L ( x , λ ) ∂ λ = A x − b = 0 \begin{aligned} \frac{\partial L(x, \lambda) }{\partial x} &= Gx+g-A\lambda = 0 \\ \frac{\partial L(x, \lambda) }{\partial \lambda} &= A^x - b = 0 \end{aligned} ∂x∂L(x,λ)∂λ∂L(x,λ)=Gx+g−Aλ=0=Ax−b=0
最优解的矩阵形式:
[ G − A − A T 0 ] [ x ∗ λ ∗ ] = − [ g b ] \begin{aligned} \begin{bmatrix} G & -A \\ -A^T & 0 \end{bmatrix} \begin{bmatrix} x^* \\ \lambda^* \end{bmatrix} =- \begin{bmatrix} g \\ b \end{bmatrix} \end{aligned} [G−AT−A0][x∗λ∗]=−[gb]
6.2 不等式约束二次规划
我们引入有效集方法 (Active Set Method, 简称 ASM)。首先显然的最优解一定成立于等式约束,或成立于不等式取等。我们可以直接枚举每一种约束条件的组合(所有等式+枚举的不等式,并将不等式看做等式约束),然后判定当前的解是否满足没有选择的不等式约束。这种方法是可行的但是计算量极大。于是有效集方法应运而生。
算法流程:
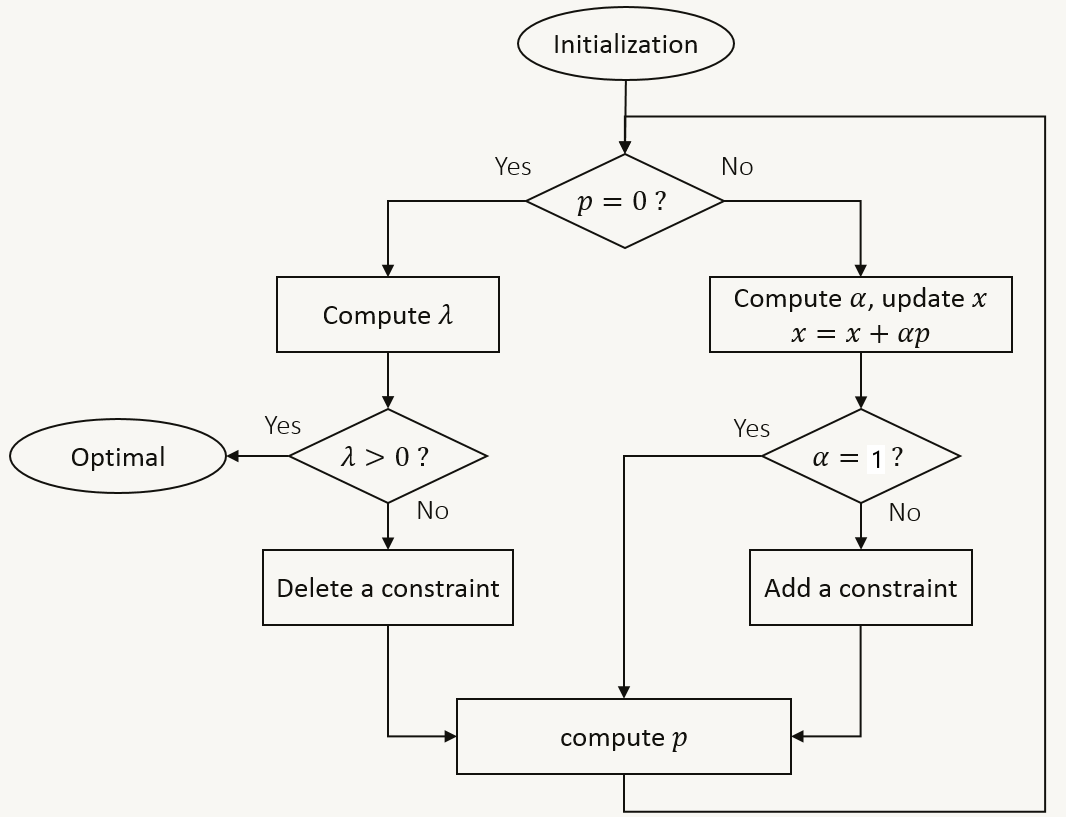
算法解析:
- 计算初始可行点 x ( 0 ) x^{(0)} x(0),可用线性规划中的大 M 法计算获得
- 计算前进方向 p k p_k pk,通过求解等式约束二次规划子问题获得
- 若 p k = 0 p_k = \bf{0} pk=0,则计算工作集约束 W k W_k Wk 对应的所有拉格朗日乘子 λ i \lambda_i λi
- 若所有 λ i ≥ 0 \lambda_i \ge 0 λi≥0,则停止迭代,得到最优解 x ∗ = x ( k ) x^*=x^{(k)} x∗=x(k)
- 若存在 λ i < 0 \lambda_i < 0 λi<0,则在工作集中剔除 λ i \lambda_i λi 最小时对应的约束 a j a_j aj,得 W k + 1 = W k ∖ { a j } W_{k+1}=W_k \setminus \set{a_j} Wk+1=Wk∖{aj}
- 若 p k ≠ 0 p_k \ne \bf{0} pk=0,则计算步长因子 α k \alpha_k αk,并置 x ( k + 1 ) = x ( k ) + α k p k x^{(k+1)} = x^{(k)} + \alpha_kp_k x(k+1)=x(k)+αkpk
- 若 α k = 1 \alpha_k=1 αk=1,则工作集不变,得 W k + 1 = W k W_{k+1}=W_k Wk+1=Wk
- 若 α k < 1 \alpha_k < 1 αk<1,则在工作集中添加 α k \alpha_k αk 最小时对应的约束 a j a_j aj,得 W k + 1 = W k ⋃ { a j } W_{k+1}=W_k \bigcup \set {a_j} Wk+1=Wk⋃{aj}
参考:
第七章「约束最优化」
{% note light %}
本章我们简单讨论约束最优化问题中,针对等式约束的「二次罚函数」算法,以及拉格朗日乘子法。
{% endnote %}
二次罚函数法
对于等式约束问题:
min f ( x ) s . t . a i ( x ) = 0 , i = 1 , 2 , . . . , p \begin{aligned} &\min\quad f(x) \\ &s.t.\quad a_i(x) = 0,\ i=1,2,...,p \end{aligned} minf(x)s.t.ai(x)=0, i=1,2,...,p
我们定义二次罚函数 P E ( x , σ ) P_E(x, \sigma) PE(x,σ),其中 σ \sigma σ 为惩罚因子:
P E ( x , σ ) = f ( x ) + 1 2 σ ∑ i = 1 p a i 2 ( x ) P_E(x, \sigma) = f(x) + \frac{1}{2} \sigma\sum_{i=1}^p a_i^2(x) PE(x,σ)=f(x)+21σi=1∑pai2(x)
不加证明的给出结论:当惩罚因子 → ∞ \to \infty →∞ 时,目标函数趋于最小值。下面给出算法流程:

拉格朗日乘子法
目标函数:
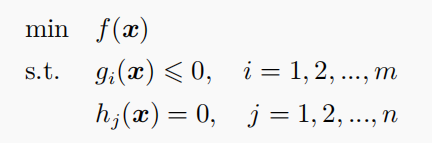
拉格朗日函数:
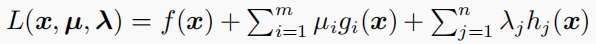
KKT 条件:

在实际求解时,我们只需要罗列上述 KKT 条件中的 (1) 和 (5),另外三个显然不需要再罗列了。我们只需要对 m m m 个不等式约束条件对应的乘子进行是否为零的讨论即可,显然需要讨论 2 m 2^m 2m 次。