神经网络的可学习性指从训练数据中自动获取最优权重参数的性质。而使得神经网络可以学习,就少不了损失函数。神经网络学习的过程可以看作是最小化损失函数的输出值的过程。换句话说,找到了最小的损失函数值,我们也就找到了一组最优的权重参数。神经网络的学习中所用的指标称为损失函数(loss function)。这个损失函数可以使用任意函数,但一般用均方误差MSE(mean squared error)和交叉熵误差(cross entropy error)等。
对于实现手写数字5识别,直接想出可以识别手写数字5的专用算法很难。如果利用机器学习技术学习数字5图像的特征量,使用人为设计的特征量(SIFT、HOG)将图像数据转换为向量,然后对其使用SVM(支持向量机)或者KNN(k近邻算法)等分类器进行学习,不失为一种方法。第三种方法是利用深度学习技术,由神经网络从收集的数据中学习,找到规律。以上三种方法的人为介入是逐渐减少的(灰色代表人未介入)。
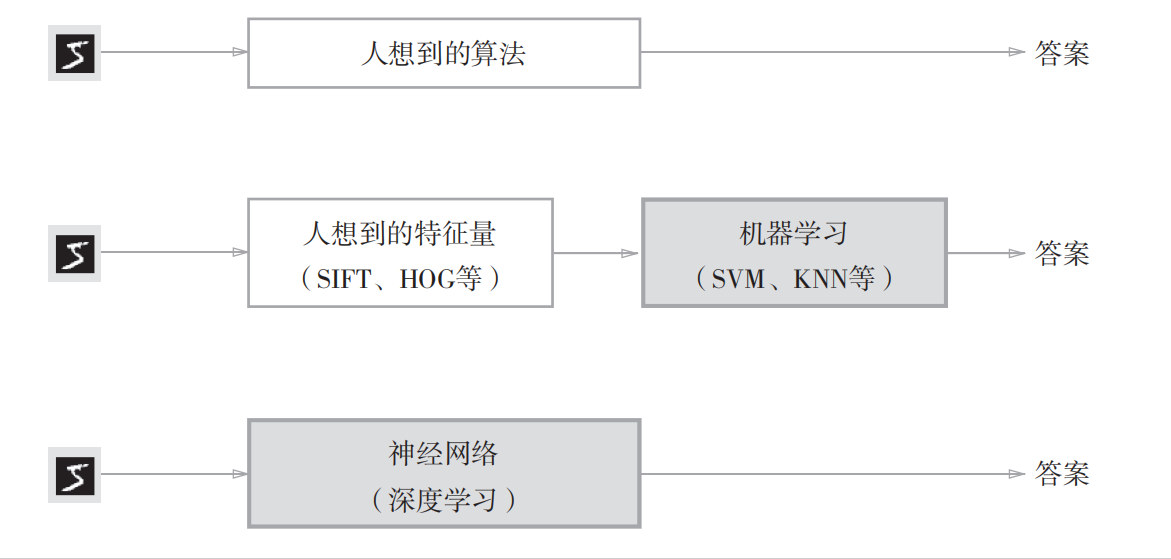
神经网络的优点是对所有的问题都可以用同样的流程来解决。无论是识别5,还是猫或人脸,其都可以通过学习所提供的数据,尝试发现待解决问题的模式。因此,神经网络解决问题与待处理的问题无关,可以将数据直接作为原始数据,进行“端对端”的学习。
在机器学习中,一般将数据分为训练数据和测试数据两部分来进行学习和实验。使用训练数据进行学习,寻找最优的参数。然后,使用测试数据评价训练得到的模型的实际能力,目的是展现模型的泛化能力。过拟合(over fitting)指的是一个模型在训练数据上表现得异常好,但在新的、未见过的数据上表现得非常差,即模型对训练数据的学习过于精确,以至于不能很好地泛化到其他数据上的情况。
1.损失函数
1.1均方误差
均方误差是最有名的损失函数,其定义如下:

yk表示神经网络的输出,tk为监督数据,k代表数据的维度。
以手写数字识别为例:
y= [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
y中十个数字依次代表神经网络输出该张图片中手写数字为0~9的概率,其中索引为2的概率最大,为0.6。而监督数据t中索引为2的位置为1,表示正确解为“2”,将正确解标签表示为1,其他标签表示为0的表示方法称为one-hot表示,也称独热编码。
那么,均方误差是如何计算的呢?根据均方误差的定义用python实现如下,并给出计算实例:
def mean_squared_error(y, t): # y和t是NumPy数组,分别对应上述的y和t
return 0.5 * np.sum((y-t)**2)
# 例子1,正确解是“2”,神经网络的输出的最大值是“2”,计算出的误差较小
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
mean_squared_error(np.array(y1), np.array(t)) # 计算出误差为0.097500000000000031
# 例子2,正确解是“2”,神经网络的输出的最大值是“7”,计算出的误差较大
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
mean_squared_error(np.array(y2), np.array(t)) # 误差为:0.59750000000000003
1.2交叉熵误差
除均方误差外,交叉熵误差(cross entropy error)也经常被用作损失函数。交叉熵误差如下式所示:
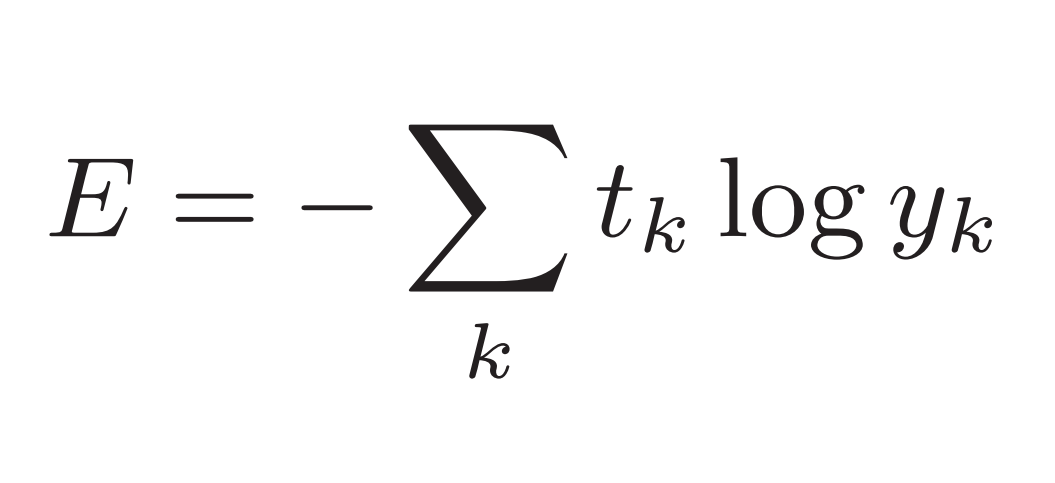
log表示以e为底数的自然对数(log e ),yk是神经网络的输出,tk是正确解标签(为独热编码)。因此,上式仅计算正确解标签对应的神经网络输出的自然对数。例如,正确解标签为“2”,与之之对应的神经网络的输出是0.6,则交叉熵误差是−log 0.6 = 0.51;若“2”对应的输出是0.1,则交叉熵误差为−log 0.1 = 2.30。也就是说,交叉熵误差的值是由正确解标签所对应的输出结果决定的。正确解标签对应的输出越大,上式的值越接近0;当神经网络对应于正确解标签的输出为1时,交叉熵误差为0。依然用上述的例子进行演示:
def cross_entropy_error(y, t):
delta = 1e-7
return -np.sum(t * np.log(y + delta)) # 添加一个微小值delta防止负无穷大(log(0))的发生
# 例子1,正确解是“2”,神经网络的输出的最大值是“2”,计算出的误差较小
y1 = [0.1, 0.05, 0.6, 0.0, 0.05, 0.1, 0.0, 0.1, 0.0, 0.0]
t = [0, 0, 1, 0, 0, 0, 0, 0, 0, 0]
cross_entropy_error(np.array(y), np.array(t)) # 计算出误差为0.51082545709933802
# 例子2,正确解是“2”,神经网络的输出的最大值是“7”,计算出的误差较大
y2 = [0.1, 0.05, 0.1, 0.0, 0.05, 0.1, 0.0, 0.6, 0.0, 0.0]
cross_entropy_error(np.array(y), np.array(t)) # 误差为:2.3025840929945458
# 与均方误差结果一致,仅误差表示方法不同!
2.损失函数的实际应用
上述的损失函数介绍只是从基本原理进行介绍,实际使用时会根据神经网络数据处理的特点进行调整。因此以下介绍mini-batch版交叉熵误差的实现。
2.1 mini-batch学习
机器学习使用训练数据进行学习,严格说就是针对训练数据计算损失函数的值,找出使该值尽可能小的参数。。因此,计算损失函数时必须将所有的训练数据作为对象。也就是说,如果训练数据有100个,我们就要把这100个损失函数的总和作为学习的指标。以交叉熵误差为例,将包含所有训练数据的损失函数定义如下:

假设数据有N个,tnk表示第n个数据的第k个元素的值(ynk是神经网络的输出,tnk是监督数据)。式子虽然看起来有一些复杂,其实只是把求单个数据的损失函数扩大到了N份数据,不过最后还要除以N进行正则化(Normalization)。通过除以N,可以求单个数据的“平均损失函数”。通过这样的平均化,可以获得和训练数据的数量无关的统一指标。 如遇到海量数据,可能会有几百万、几千万之多,这种情况下以全部数据为对象计算损失函数是不现实的。因此需要从全部数据中选出一部分,作为全部数据的“近似”。神经网络的学习也是从训练数据中选出一批数据(称为mini-batch,小批量),然后对每个mini-batch进行学习。比如,从60000个训练数据中随机选择100批(每批600张手写数字图片),再用这100批数据进行学习,这种学习方式称为mini-batch学习。
编写从训练数据中随机选择指定个数的数据的代码,从而进行mini-batch学习。
import sys, os
sys.path.append(os.pardir)
import numpy as np
from dataset.mnist import load_mnist # load_mnist函数是用于读入MNIST数据集
(x_train, t_train), (x_test, t_test) = \
load_mnist(normalize=True, one_hot_label=True)
print(x_train.shape) # 训练数据 (60000, 784)
print(t_train.shape) # 监督数据 (60000, 10)
train_size = x_train.shape[0] # train_size = 60000
batch_size = 10
batch_mask = np.random.choice(train_size, batch_size) # np.random.choice()可以从指定的数字中随机选择想要的数字
x_batch = x_train[batch_mask]
t_batch = t_train[batch_mask]
# 我们只需指定这些随机选出的索引,取出mini-batch,然后使用这个mini-batch计算损失函数即可。
2.2 mini-batch版交叉熵误差的实现
如何实现对应mini-batch的交叉熵误差呢?首先实现一个可以同时处理单个数据和批量数据(数据作为batch集中输入)两种情况的函数。
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(t * np.log(y + 1e-7)) / batch_size
# 当监督数据是标签形式(非one-hot表示)时,交叉熵误差可通过如下代码实现
def cross_entropy_error(y, t):
if y.ndim == 1:
t = t.reshape(1, t.size)
y = y.reshape(1, y.size)
batch_size = y.shape[0]
return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size
# np.arange (batch_size)会生成一个从0到batch_size-1的数组。比如当batch_size为5时,np.arange(batch_size)会生成一个NumPy 数组[0, 1, 2, 3, 4]。因为t中标签是以[2, 7, 0, 9, 4]的形式存储的,所以y[np.arange(batch_size), t]能抽出各个数据的正确解标签对应的神经网络的输出(在这个例子中,y[np.arange(batch_size), t] 会生成 NumPy 数 组 [y[0,2], y[1,7], y[2,0],y[3,9], y[4,4]])。
为什么要导入损失函数呢?不应该把识别精度作为指标吗?在神经网络的学习中,寻找最优参数(权重和偏置)时,要寻找使损失函数的值尽可能小的参数。为了找到使损失函数的值尽可能小的地方,需要计算参数的导数(确切地讲是梯度),然后以这个导数为指引,逐步更新参数的值。
假设有一个神经网络,关注这个神经网络中的某一个权重参数。此时,对该权重参数的损失函数求导表示的是“如果稍微改变这个权重参数的值,损失函数的值会如何变化”。如果导数的值为负,通过使该权重参数向正方向改变,可以减小损失函数的值;反过来,如果导数的值为正,则通过使该权重参数向负方向改变,可以减小损失函数的值。不过,当导数的值为0时,无论权重参数向哪个方向变化,损失函数的值都不会改变,此时该权重参数的更新会停在此处。之所以不能用识别精度作为指标,是因为这样一来绝大多数地方的导数都会变为0,导致参数无法更新。
为什么用识别精度作为指标时,参数的导数在绝大多数地方都会变成0呢?为了回答这个问题,思考另一个具体例子。假设某个神经网络正确识别出了100批训练数据中的32笔,此时识别精度为32 %。如果以识别精度为指标,即使稍微改变权重参数的值,识别精度也仍将保持在32 %,不会出现变化。也就是说,仅仅微调参数,是无法改善识别精度的。即便识别精度有所改善,它的值也不会像32.0123 ... %这样连续变化,而是变为33 %、34 %这样的不连续的、离散的值。而如果把损失函数作为指标,则当前损失函数的值可以表示为0.92543...这样的值。并且,如果稍微改变一下参数的值,对应的损失函数也会像0.93432...这样发生连续性的变化。
识别精度对微小的参数变化基本上没有什么反应,即便有反应,它的值也是不连续地、突然地变化。作为激活函数的阶跃函数也有同样的情况。出于相同的原因,如果使用阶跃函数作为激活函数,神经网络的学习将无法进行。
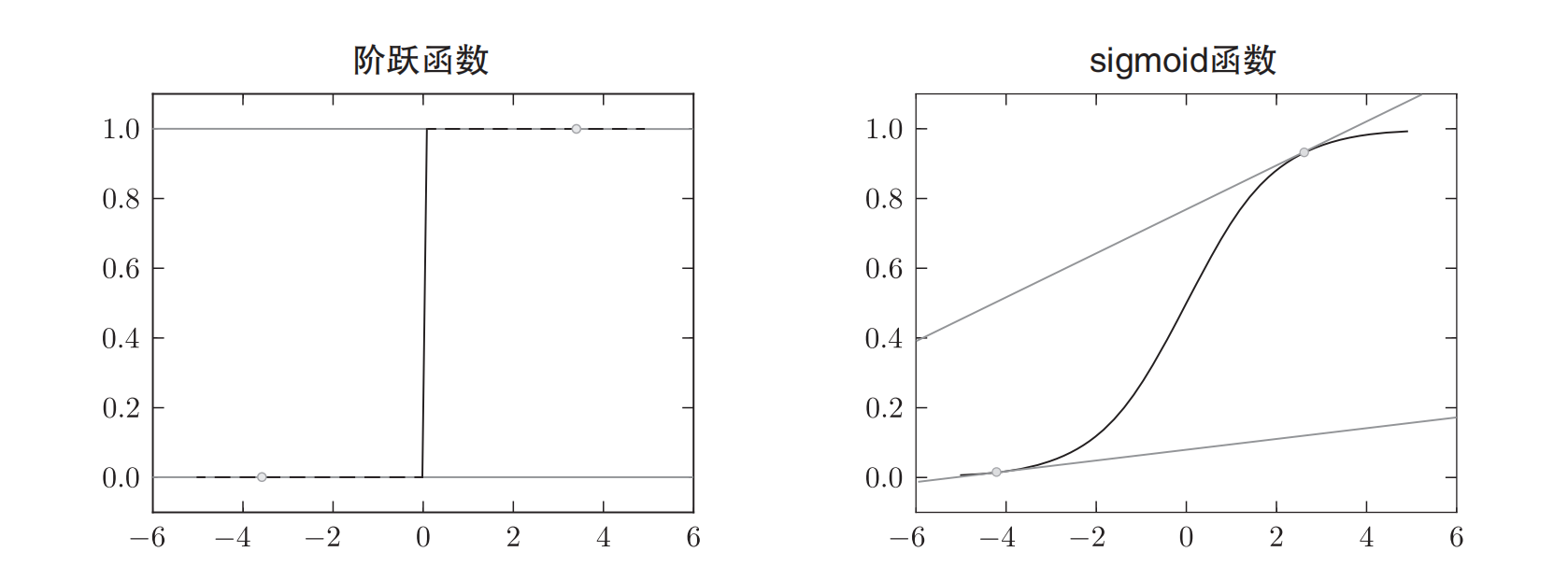
阶跃函数就像“竹筒敲石”一样,只在某个瞬间产生变化。而sigmoid函数,如上图所示,不仅函数的输出(竖轴的值)是连续变化的,曲线的斜率(导数)也是连续变化的。也就是说,sigmoid函数的导数在任何地方都不为0。这对神经网络的学习非常重要。得益于这个斜率不会为0的性质,神经网络的学习得以正确进行。