C++树（二）【直径，中心】

目录：

树的直径：

树的直径的性质： 

性质1：直径的端点一定是叶子节点                

性质2：任意点的最长链端点一定是直径端点。

性质3：如果一棵树有多条直径,那么它们必然相交，且有极长连续段（可以是一个点，交点为树的中心）

性质4：树T1的直径为x,y，树T2的直径为s,t。现有一边u,v与两颗树相连，新树的直径端点一点是x,y,s,t中的两个

树的直径求解方法：

树的直径的端点

树的中心

树的中心求解：

树的中心两个性质：

        证明：

公共点公共边的求法：

总结：

一、树的直径的四个基础性质

二、树的直径相关求解问题

树的直径：

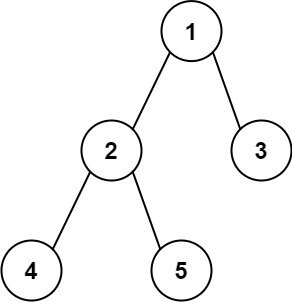
定义：树的直径是树上两点间距离的最大值。即树中最远的两个节点之间的距离被称为树的直径，连接这两点的路径被称为树的最长链。

链1) 5- 7 - 8 -3

链2) 1- 4 - 7 - 8 - 3

直径为17

树的直径的性质： 

性质1：直径的端点一定是叶子节点                

        证明：假设直径s-t外存在一点p相连->s-t-p st+tp>st<sp   不成立

性质2：任意点的最长链端点一定是直径端点。

        证明：

性质3：如果一棵树有多条直径,那么它们必然相交，且有极长连续段（可以是一个点，交点为树的中心）

        证明：

性质4：树T1的直径为x,y，树T2的直径为s,t。现有一边u,v与两颗树相连，新树的直径端点一点是x,y,s,t中的两个

证明：

         性质4分析：

uv连接后有两种情况

1.新直径不过uv，即现直径为st或为xy。2.新直径过uv，则现直径为

max(vs,vt)+max(ux,uy)+uv。

这两种情况都能保证新直径端点为x,y,s,t中的任意两个。新直径为以上三个中最大值。

        连边uv求新树直径最小：

引理性质4可知：

st与xy不变，此时只能减下过uv的直径大小。以max(vs,vt)为例，要使该值最小，则v应当在树的中心位置，这样vs与vt越均衡。

同理u也应该在T2的树的中心位置。

        连边uv求新树直径最大：

与前面一致，以max(vs,vt)为例，要使得该值最大，则v应当选择直径端点位置。

因此uv选择各自直径的端点位置时，直径最大。

树的直径求解方法：

引理性质2：任意点的最长链端点一定是直径端点。

方法：随意找一个点x,进行dfs找到最长链的端点s,再以端点s做第二遍dfs，此时可以找到直径的第二个端点t。此时端点s到t的距离就是树的直径。

树的直径的端点

通过记录父亲节点的方式能够把直径上的所有点全部记录下来。

在树中，直径端点是常用点(假设端点为s,t)，我们树上任意一点p所能到的最大距离，只有可能是到ps或pt

找到所有点到两个直径端点的距离方法

法一（朴素方法）:

        求出直径端点后，以每个点为根做dfs，找到根节点到端点的距离。

        复杂度O(N2)。

法二（优化方法）：

        第一次从任意点出发，必然能到达直径的一个端点s。

        第二次从s点进行dfs找到端点t，此时记录所有点到s的距离。

        第三次从t点进行dfs，记录所有点到t的距离。

        复杂度：O(n)

树的中心

概念：以树的中心为根时，从该根到每个叶子节点的最长路径最短，使得路径和平衡。

树的中心求解：

        我们现在已经知道求解任意一点到两端点的距离，即根据性质2可很轻松得到每个点能到的最长路径。求出每个点后的路径后，一次遍历便可知树的中心点。

树的中心两个性质：

性质1：树的中心一定在直径上，且趋向于中点位置

性质2：树的中心可以有一个(单中心)，也可以有两个(双中心)

        证明：

引理性质2，若树的中心p不在直径st上，st上有一点q与直径联通。中心点能到的最远距离为：

max(qs,qt)+pq，若要使得该值最小，pq应当为0，因此p在直径上。

同时为了让max(qs,qt)更小，树的中心要在直径中点处。

直径公共点证明与求解方法

以当一颗树存在多条直径时，引理性质3，公共边一定连续，因此可以直接对公共点/边进行求解

公共点公共边的求法：

        找到直径左右端点s,t，从左往右遍历直径上的点进行

        dfs，如果某点r在直径外找到一点与到右端点t距离相同，点r右边的点一定不是公共点。

        同理，从右往左遍历直径上的点进行dfs，如果某点l在直径外找到一点与到左端点s距离相同，l左边的点一定不是公共点。此时，l->r就是我们直径的公共点。

        因此我们只需要找到公共点边界l,r即可。使得l尽可能靠右，r尽可能靠左。

总结：

一、树的直径的四个基础性质

性质1：直径的端点一定是叶子节点

性质2：任意点的最长链端点一定是直径端点

性质3：如果一棵树有多条直径,那么它们必然相交，且有极长连续段

性质4：两颗树加一条边相连，构成的新树直径端点一点是x,y,s,t中的两个

二、树的直径相关求解问题

1. 树的直径以及所有点到直径左右端点距离的解法。

2. 树的中心的含义以及求解方法。

3. 直径的公共点/边的求解方法。

4. 两颗树连边后求新树的最小/大直径方法。