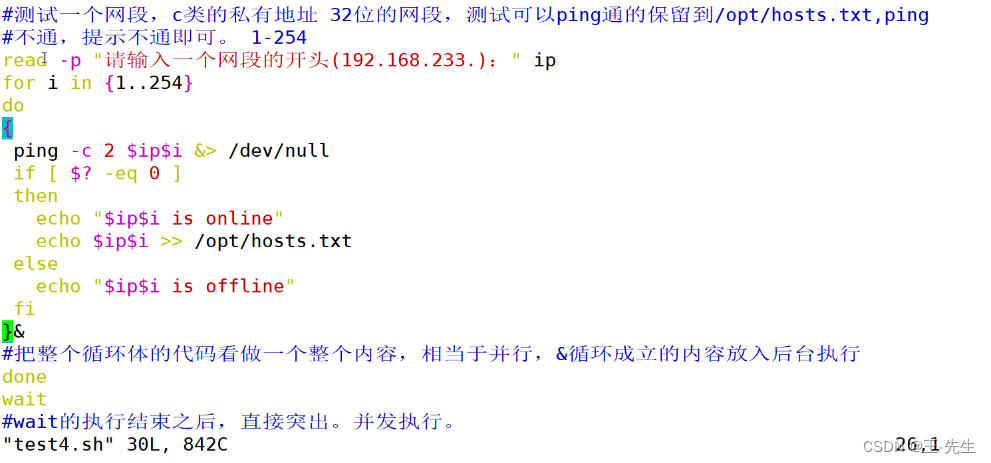
以下是一个简单的二叉搜索树实现,包括插入和查找操作的示例代码:
#include <iostream>
// 定义二叉搜索树的节点结构
struct TreeNode {
int val;
TreeNode *left;
TreeNode *right;
TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
};
// 二叉搜索树类
class BinarySearchTree {
public:
BinarySearchTree() : root(nullptr) {}
// 插入操作
void insert(int val) {
root = insertRecur(root, val);
}
// 查找操作
bool find(int val) const {
return findRecur(root, val) != nullptr;
}
private:
TreeNode *root;
// 递归插入操作
TreeNode* insertRecur(TreeNode* node, int val) {
if (!node) {
return new TreeNode(val);
}
if (val < node->val) {
node->left = insertRecur(node->left, val);
} else if (val > node->val) {
node->right = insertRecur(node->right, val);
}
// 如果val已经存在,则不插入
return node;
}
// 递归查找操作
TreeNode* findRecur(TreeNode* node, int val) const {
if (!node || node->val == val) {
return node;
}
if (val < node->val) {
return findRecur(node->left, val);
} else {
return findRecur(node->right, val);
}
}
};
// 面试时,你可以解释这段代码,并讨论二叉搜索树的各种操作。
int main() {
BinarySearchTree bst;
bst.insert(50);
bst.insert(30);
bst.insert(20);
bst.insert(40);
bst.insert(70);
bst.insert(60);
bst.insert(80);
if (bst.find(60)) {
std::cout << "Found 60 in the BST." << std::endl;
} else {
std::cout << "60 is not in the BST." << std::endl;
}
return 0;
}
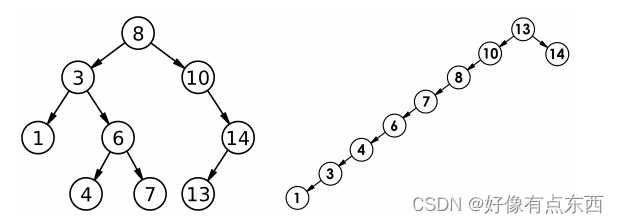
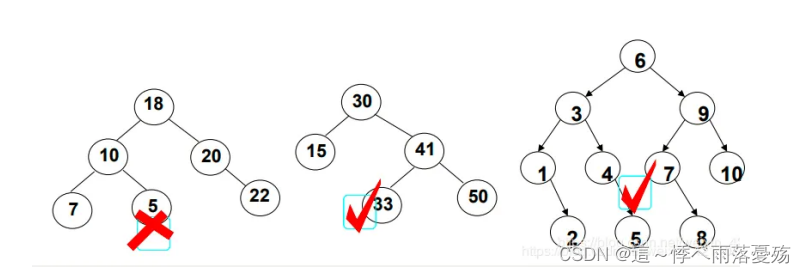
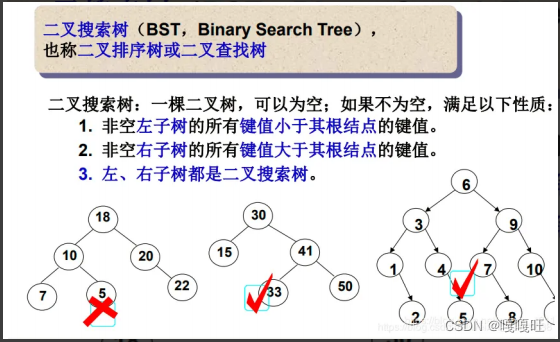
二叉搜索树的特点:
有序性:对于BST中的任意节点,其左子树上所有节点的值均小于该节点的值,右子树上所有节点的值均大于该节点的值。
二叉树结构:每个节点最多有两个子节点,通常左子节点称为左子树,右子节点称为右子树。
动态数据结构:二叉搜索树可以在运行时动态地添加和删除节点。
时间复杂度:在平衡的情况下,BST的查找、插入和删除操作的时间复杂度为O(log n)。但在最坏的情况下(例如,树退化为链表),时间复杂度为O(n)。
遍历方式:BST可以通过中序遍历(In-Order Traversal)来实现有序遍历。
二叉搜索树的实现要点:
节点定义:通常使用一个结构体或类来定义树的节点,包含数据域和指向左右子节点的指针。
插入操作:根据BST的特性,递归地将新节点插入到正确的位置。
查找操作:从根节点开始,根据目标值与当前节点值的比较结果,决定是向左子树还是向右子树搜索。
删除操作:删除节点稍微复杂,需要考虑三种情况:无子节点、有一个子节点、有两个子节点。
平衡问题:为了保持BST的高效性,需要考虑平衡问题,可以使用AVL树或红黑树等自平衡二叉搜索树。
面试回答示例:
"二叉搜索树是一种非常有效的数据结构,用于快速查找、插入和删除操作。它的核心特点是每个节点的值都大于其左子树上所有节点的值,小于其右子树上所有节点的值。这保证了二叉搜索树可以进行中序遍历,从而获得有序的数据序列。
在实现BST时,我们需要定义一个节点结构,包含数据域和指向左右子节点的指针。插入操作是通过递归地比较节点值来完成的。查找操作则是从根节点开始,根据目标值与当前节点值的比较结果,决定搜索的方向。
然而,如果不考虑平衡,二叉搜索树在最坏的情况下可能会退化成链表,导致操作的时间复杂度退化为O(n)。为了解决这个问题,我们可以使用平衡二叉搜索树,如AVL树或红黑树,它们通过旋转操作来保持树的平衡,确保所有操作的时间复杂度接近O(log n


![[<span style='color:red;'>C</span>++]<span style='color:red;'>二</span><span style='color:red;'>叉</span><span style='color:red;'>搜索</span><span style='color:red;'>树</span>](https://img-blog.csdnimg.cn/direct/6a5be3369a064765bb55ef13cb9d8460.png)

























![[巨详细]安装HBuilder-X教程](https://img-blog.csdnimg.cn/b161eb27bad34615904c5600b4108e58.gif#pic_center)