目标
在这个实验中,你将:
- 使用梯度下降自动优化 w w w 和 b b b 的过程。
Tools
import math, copy
import numpy as np
import matplotlib.pyplot as plt
plt.style.use('./deeplearning.mplstyle')
from lab_utils_uni import plt_house_x, plt_contour_wgrad, plt_divergence, plt_gradients
怎么理解:
import math, copyimport math, copy这行代码是Python中的导入语句,它用于导入两个不同的模块:math和copy。math模块提供了许多数学函数和常数,例如三角函数、对数函数等。通过导入math模块,你可以使用这些函数而无需自己实现。例如,你可以使用math.sin()函数来计算正弦值,math.sqrt()函数来计算平方根等。copy模块提供了用于复制对象的函数。在Python中,赋值操作通常是对象的引用,这意味着当你将一个对象赋值给另一个变量时,它们实际上指向相同的内存地址。使用copy模块可以创建对象的浅拷贝或深拷贝,从而在需要时避免修改原始对象。例如,你可以使用copy.copy()函数创建一个对象的浅拷贝,或者使用copy.deepcopy()函数创建一个对象的深拷贝。
浅拷贝和深拷贝是什么
浅拷贝(shallow copy)和深拷贝(deep copy)是在Python中用于复制对象的两种不同方式。
- 浅拷贝:
- 浅拷贝创建一个新对象,其内容是原始对象的引用。这意味着新对象的顶层元素是原始对象中元素的引用,而不是元素的副本。
- 对于可变对象(如列表、字典等),浅拷贝将创建一个新对象,但是新对象中的可变元素仍然与原始对象共享。这意味着修改新对象中的可变元素也会影响原始对象中的元素。
- 浅拷贝可以通过
copy.copy()函数实现。
- 深拷贝:
- 深拷贝创建一个完全独立于原始对象的新对象,包括对象的所有内容。这意味着即使原始对象是嵌套的,新对象中的所有元素也都是副本,而不是引用。
- 无论对象的层级结构多深,深拷贝都会递归地复制整个对象树。
- 深拷贝可以通过
copy.deepcopy()函数实现。
在选择使用浅拷贝还是深拷贝时,需要考虑对象的结构以及是否需要修改新对象而不影响原始对象。通常情况下,如果对象中包含嵌套的可变对象,并且你不希望修改新对象会影响原始对象,那么应该使用深拷贝。如果对象结构较简单,或者你希望新对象与原始对象共享部分内容,那么可以使用浅拷贝。
- 浅拷贝:
问题陈述
让我们继续使用之前的两个数据点:
| 面积(1000平方英尺) | 价格(千美元) |
|---|---|
| 1 | 300 |
| 2 | 500 |
# Load our data set
x_train = np.array([1.0, 2.0]) #features
y_train = np.array([300.0, 500.0]) #target value
计算代价
这是在上一个实验中开发的。我们将在这里再次需要它。
# 计算代价函数
def compute_cost(x, y, w, b):
m = x.shape[0] # 样本数量
cost = 0
for i in range(m):
f_wb = w * x[i] + b # f_wb:预测的函数值
cost = cost + (f_wb - y[i])**2
total_cost = 1 / (2 * m) * cost
return total_cost
梯度下降总结
到目前为止,在这门课程中,你已经开发了一个线性模型,用于预测 f w , b ( x ( i ) ) f_{w,b}(x^{(i)}) fw,b(x(i)):
f w , b ( x ( i ) ) = w x ( i ) + b (1) f_{w,b}(x^{(i)}) = wx^{(i)} + b \tag{1} fw,b(x(i))=wx(i)+b(1)
在线性回归中,你利用输入训练数据来拟合参数 w , b w,b w,b,通过最小化我们的预测值 f w , b ( x ( i ) ) f_{w,b}(x^{(i)}) fw,b(x(i)) 和实际数据 y ( i ) y^{(i)} y(i) 之间的误差度量来完成。
这个度量被称为 c o s t cost cost, J ( w , b ) J(w,b) J(w,b)。在训练中,你测量所有训练样本 x ( i ) , y ( i ) x^{(i)},y^{(i)} x(i),y(i) 上的代价:
J ( w , b ) = 1 2 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) 2 (2) J(w,b) = \frac{1}{2m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})^2\tag{2} J(w,b)=2m1i=0∑m−1(fw,b(x(i))−y(i))2(2)
在讲座中,梯度下降算法 被描述为:
repeat until convergence: { w = w − α ∂ J ( w , b ) ∂ w b = b − α ∂ J ( w , b ) ∂ b } (3) \text{repeat until convergence:} \lbrace \\ \; w = w - \alpha \frac{\partial J(w,b)}{\partial w} \tag{3} \\ b = b - \alpha \frac{\partial J(w,b)}{\partial b} \\ \rbrace repeat until convergence:{w=w−α∂w∂J(w,b)b=b−α∂b∂J(w,b)}(3)
其中,参数 w , b w,b w,b 同时被更新。直到 w 、 b w、b w、b 不再因为额外的步骤而发生很大的变化。
∂ J ( w ) ∂ w i \frac{\partial J(\mathbf{w})}{\partial w_i} ∂wi∂J(w) 的意义
它告诉我们在当前参数值下,代价函数值的变化方向和速率。具体来说,偏导数 ∂ J ( w ) ∂ w i \frac{\partial J(\mathbf{w})}{\partial w_i} ∂wi∂J(w) 表示了当参数 w i w_i wi 发生微小变化时,代价函数 J ( w J(\mathbf{w} J(w) 的变化率。如果偏导数为正,意味着增加 w i w_i wi 会导致代价函数增加,我们应该减小 w i w_i wi;如果偏导数为负,意味着增加 w i w_i wi 会导致代价函数减小,我们应该增大 w i w_i wi。
通过梯度下降等优化算法,我们可以沿着代价函数的负梯度方向逐步更新参数 w \mathbf{w} w,直到找到使代价函数最小化的参数值。因此,代价函数对参数 w \mathbf{w} w 求偏导的意义在于指导优化算法寻找最优的参数值,从而使模型的预测更准确。
理解梯度下降
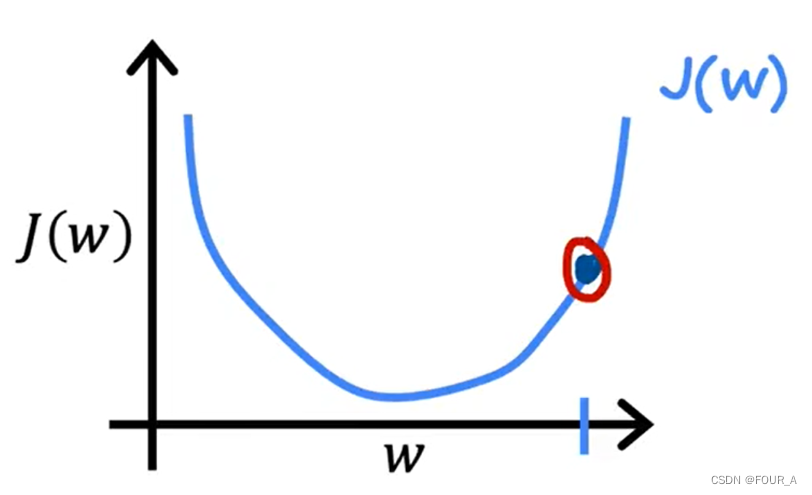
将函数简化为二维,即 b = 0 b = 0 b=0 时,
假设一开始 w w w 在红圈处,记为 w = w 0 w=w_0 w=w0
此时根据梯度下降的公式: w = w − α ∂ J ( w , b ) ∂ w w = w - \alpha \frac{\partial J(w,b)}{\partial w} w=w−α∂w∂J(w,b)
由于 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 为 J ( w ) J(w) J(w) 在 w = w 0 w=w_0 w=w0 处的切线斜率,显然为正数
则, w w w 的值显然会减小,即朝着使 J ( w ) J(w) J(w) 更小的方向去了
梯度被定义为:
∂ J ( w , b ) ∂ w = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) x ( i ) (4) \frac{\partial J(w,b)}{\partial w} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)})x^{(i)} \tag{4}\\ ∂w∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))x(i)(4)
∂ J ( w , b ) ∂ b = 1 m ∑ i = 0 m − 1 ( f w , b ( x ( i ) ) − y ( i ) ) (5) \frac{\partial J(w,b)}{\partial b} = \frac{1}{m} \sum\limits_{i = 0}^{m-1} (f_{w,b}(x^{(i)}) - y^{(i)}) \tag{5}\\ ∂b∂J(w,b)=m1i=0∑m−1(fw,b(x(i))−y(i))(5)
这里的 同时 意味着在更新任何参数之前,你计算所有参数的偏导数。
实现梯度下降
你将为一个特征实现梯度下降算法。你需要三个函数。
compute_gradient实现上述方程 (4) 和 (5)compute_cost实现上述方程 (2)(来自前一个实验室的代码)gradient_descent,利用compute_gradient和compute_cost
约定:
- 包含偏导数的Python变量命名遵循这种模式, ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 将被命名为
dj_db。 - w.r.t 是 With Respect To 的缩写,表示对于,即 J ( w b ) J(wb) J(wb) 的偏导数 With Respect To b b b。
计算梯度
compute_gradient 实现了上述 (4) 和 (5) 并返回 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b), ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b)。嵌入式注释描述了操作。
def compute_gradient(x, y, w, b):
# Number of training examples
m = x.shape[0] # m : 样例的个数
dj_dw = 0
dj_db = 0
for i in range(m):
f_wb = w * x[i] + b # f_wb:预测值
dj_dw_i = (f_wb - y[i]) * x[i] # j对w求偏导
dj_db_i = f_wb - y[i] # j对b求偏导
# 偏导求和
dj_db += dj_db_i
dj_dw += dj_dw_i
dj_dw = dj_dw / m
dj_db = dj_db / m
return dj_dw, dj_db
讲座描述了梯度下降如何利用代价相对于某个参数的偏导数在某一点来更新该参数。
让我们使用我们的 compute_gradient 函数来找到并绘制成本函数相对于其中一个参数 w 0 w_0 w0 的一些偏导数。
plt_gradients(x_train,y_train, compute_cost, compute_gradient)
plt.show()
解释一下:
plt_gradients(x_train,y_train, compute_cost, compute_gradient)这个函数的目的是帮助你可视化代价函数相对于参数 w 0 w_0 w0 的变化情况,从而更好地理解梯度下降算法如何更新参数以最小化代价函数。
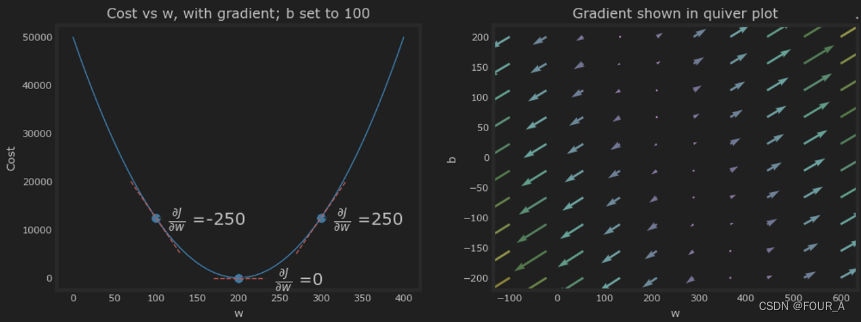
上面,左图显示了 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b),即在三个点处相对于 w w w 的成本曲线的斜率。在图的右侧,导数为正,而在左侧导数为负。由于 ‘碗形’ 的形状,导数将始终引导梯度下降向着梯度为零的底部。
左图中, b = 100 b=100 b=100 是固定的。梯度下降将利用 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 和 ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b) 来更新参数。
右侧的 quiver plot 提供了查看两个参数的梯度的方法。
箭头的大小反映了该点处梯度的大小。
箭头的方向和斜率反映了该点处 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 和 ∂ J ( w , b ) ∂ b \frac{\partial J(w,b)}{\partial b} ∂b∂J(w,b)的比率。
请注意,梯度指向 远离 最小值。请回顾上述方程 (3)。在当前值 w w w 或 b b b 上 减去 缩放后的梯度。这将使参数朝着降低代价的方向移动。
梯度下降
现在可以计算梯度了,在上述方程 (3) 中描述的梯度下降可以在下面的 gradient_descent 中实现。实现的细节在注释中描述。在下面,你将利用这个函数在训练数据上找到 w w w 和 b b b 的最优值。
def gradient_descent(x, y, w_in, b_in, alpha, num_iters, cost_function, gradient_function):
w = copy.deepcopy(w_in) # 避免修改了原始的 w,因为 w 和 b 要同时计算
J_history = [] #用于保存每次迭代后的成本值
p_history = [] #用于保存每次迭代后的参数 w 和 b 的数值
# b_in 是传入的初始偏置值,而 b 则是在梯度下降过程中实时更新的偏置值。
b = b_in
# w_in 是传入的初始权重值,而 w 则是在梯度下降过程中实时更新的权重值
w = w_in
# num_iters:迭代的总次数,即梯度下降算法将执行的总迭代次数。
for i in range(num_iters):
# gradient_function函数的作用是计算成本函数相对于权重 w 和偏置 b 的偏导数
# 即之前已经写好的函数:compute_gradient
dj_dw, dj_db = gradient_function(x, y, w , b)
# 使用上面的方程(3)更新参数
b = b - alpha * dj_db
w = w - alpha * dj_dw
# 在每次迭代过程中保存成本函数 J 的值
if i<100000: # 避免资源耗尽问题,即在大规模迭代时不会占用太多内存或计算资源。
#这行代码将当前迭代后计算得到的代价函数值,即 J(w,b),添加到名为 J_history 的列表中。
J_history.append( cost_function(x, y, w , b))
# 这行代码将当前迭代后的参数w和b的数值,以列表 [w,b] 的形式添加到名为 p_history 的列表中。
p_history.append([w,b])
# 用于在每隔一定的迭代次数输出迭代过程中的一些信息
# 包括当前迭代次数、成本函数值、权重和偏置的梯度值,以及更新后的权重和偏置值。
if i % math.ceil(num_iters/10) == 0:
print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e} ",
f"dj_dw: {dj_dw: 0.3e}, dj_db: {dj_db: 0.3e} ",
f"w: {w: 0.3e}, b:{b: 0.5e}")
return w, b, J_history, p_history
解释一下:
i % math.ceil(num_iters/10) == 0这部分代码是用来检查当前迭代次数是否是总迭代次数的十分之一的倍数。
这样做的目的是为了控制输出信息的频率,使得输出信息不会太频繁,同时能够在迭代过程中观察到一些关键的信息。
解释一下:
print(f"Iteration {i:4}: Cost {J_history[-1]:0.2e}这部分代码是使用 Python 的
f-string格式化字符串功能,用来打印每次迭代的信息。具体来说,它会输出当前迭代次数
i、最新的成本函数值J_history[-1]。:4和:0.2e分别表示将i和J_history[-1]的值格式化为占据四个字符宽度的整数和科学计数法形式的浮点数。解释一下:
return w, b, J_history, p_history这部分代码使用
return语句返回了四个值:w、b、J_history和p_history。这些值将作为函数的输出,可以在函数被调用的地方进行使用。具体来说:w: 是经过梯度下降算法迭代更新后得到的最终权重值。b: 是经过梯度下降算法迭代更新后得到的最终偏置值。J_history: 是一个列表,包含了每次迭代后的成本函数值。p_history: 是一个列表,包含了每次迭代后的参数w和b的数值。
这些返回值可以用于进一步的分析、可视化以及其他需要使用这些结果的操作。
# 将初始的权重 w_init 和偏置 b_init 分别设为 0。
w_init = 0
b_init = 0
# 将迭代次数设置为 10000 次
iterations = 10000
# 将学习率设置为 0.01
tmp_alpha = 1.0e-2
# 调用 gradient descent 函数
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,
iterations, compute_cost, compute_gradient)
print(f"(w,b) found by gradient descent: ({w_final:8.4f},{b_final:8.4f})")
请稍作注意,并注意上面打印出的梯度下降过程的一些特点。
- 成本从一个较大的值开始,随着时间的推移迅速下降,就像讲座中所描述的那样。
- 偏导数
dj_dw和dj_db也在迅速减小,起初速度很快,然后逐渐变慢。正如讲座中所示的那样,随着过程接近 ‘碗底’,进展变得更慢,这是由于该点处导数的值较小。 - 尽管学习率 alpha 保持不变,但进展变慢。
代价与梯度下降迭代次数的关系图
代价与梯度下降迭代次数的关系图是衡量梯度下降进展的有用指标。在成功运行中,成本应始终下降。成本的变化在最初是如此迅速,因此在不同的比例上绘制初始下降与最终下降是有用的。请注意下面图表中的成本轴的比例和迭代步骤。
# plot cost versus iteration
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))
ax1.plot(J_hist[:100])
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])
ax1.set_title("Cost vs. iteration(start)"); ax2.set_title("Cost vs. iteration (end)")
ax1.set_ylabel('Cost') ; ax2.set_ylabel('Cost')
ax1.set_xlabel('iteration step') ; ax2.set_xlabel('iteration step')
plt.show()
解释一下:
fig, (ax1, ax2) = plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))这行代码创建了一个包含两个子图的图形窗口。具体来说:
plt.subplots(1, 2, constrained_layout=True, figsize=(12,4))创建了一个包含一行两列的子图布局,即创建了两个子图。- 参数
constrained_layout=True表示自动调整子图布局以防止重叠 - 参数
figsize=(12,4)设置了图形窗口的大小为宽度 12 英寸、高度 4 英寸。 fig, (ax1, ax2)分别返回了整个图形窗口对象和两个子图对象ax1和ax2,可以通过这两个对象分别对两个子图进行操作。
解释一下:
ax1.plot(J_hist[:100])这行代码在第一个子图
ax1上绘制了代价函数随迭代次数的变化曲线。具体来说,ax1.plot(J_hist[:100])绘制了J_hist列表中前 100 个元素对应的曲线。这个曲线显示了梯度下降算法在初始阶段的成本函数值随着迭代次数的变化情况。解释一下:
ax2.plot(1000 + np.arange(len(J_hist[1000:])), J_hist[1000:])plot函数的两个参数分别是:- x 轴数据:
1000 + np.arange(len(J_hist[1000:]))1000是为了从 1000 开始计数,因为我们从第 1000 个元素开始记录成本函数值。np.arange(len(J_hist[1000:]))生成一个等差数列,长度与J_hist[1000:]的长度相同,表示迭代次数。
- y 轴数据:
J_hist[1000:]J_hist[1000:]表示从第 1000 个元素开始到最后一个元素的成本函数值,用于绘制曲线。
- x 轴数据:
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传
预测
现在你已经发现了参数 w w w 和 b b b 的最优值,你可以使用模型根据我们学到的参数来预测房屋价值。正如预期的那样,预测值与相同房屋的训练值几乎相同。此外,预测中未包含的值与预期值一致。
# 这段代码用于打印根据学到的参数进行的房屋价值预测
print(f"1000 sqft house prediction {w_final*1.0 + b_final:0.1f} Thousand dollars")
print(f"1200 sqft house prediction {w_final*1.2 + b_final:0.1f} Thousand dollars")
print(f"2000 sqft house prediction {w_final*2.0 + b_final:0.1f} Thousand dollars")
绘图
你可以通过绘制代价函数随迭代次数的变化曲线,并在成本函数 J ( w , b ) J(w,b) J(w,b) 的等高线图上显示梯度下降的进展情况。
fig, ax = plt.subplots(1,1, figsize=(12, 6))
# 在参数空间中绘制代价函数 J(w, b) 的等高线图,并在图中显示梯度下降过程中的参数**更新路径**
plt_contour_wgrad(x_train, y_train, p_hist, ax)
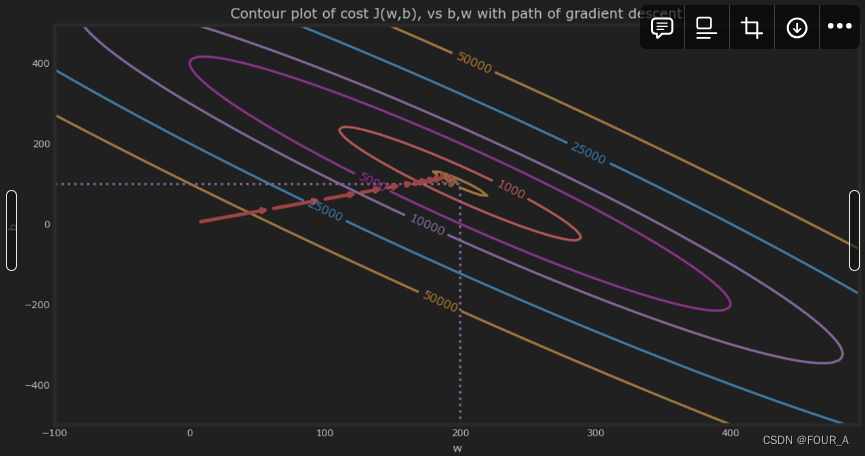
上面的等高线图显示了在一定范围内 w w w 和 b b b 的成本函数 J ( w , b ) J(w,b) J(w,b)。成本水平由等高线表示。叠加在图上的是梯度下降的路径,用红色箭头表示。以下是一些需要注意的事项:
- 路径朝着目标稳定(单调)地前进。
- 初始步长比接近目标时的步长要大得多。
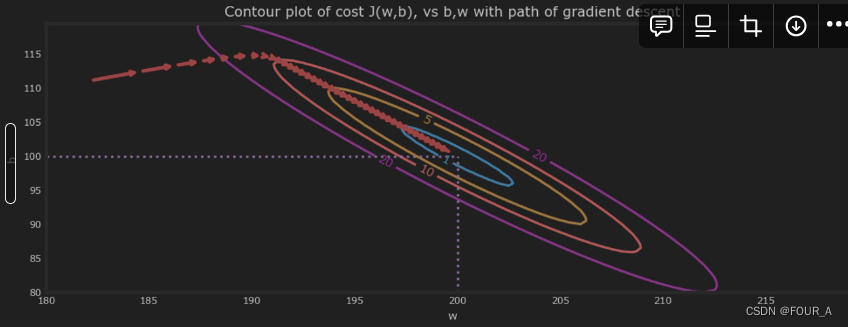
放大后,我们可以看到梯度下降的最后几步。注意随着梯度接近零,步长之间的距离在缩小。
fig, ax = plt.subplots(1,1, figsize=(12, 4))
plt_contour_wgrad(x_train, y_train, p_hist, ax, w_range=[180, 220, 0.5], b_range=[80, 120, 0.5],
contours=[1,5,10,20],resolution=0.5)
# contours=[1,5,10,20] 指定了要显示的等高线的值。
# resolution=0.5 指定了等高线图的分辨率。
增大学习率
在讲座中,有关方程(3)中学习率 α \alpha α 的合适值的讨论。 α \alpha α 越大,梯度下降收敛到解的速度越快。但是,如果它太大,梯度下降会发散。上面是一个收敛良好的解的示例。
让我们尝试增大 α \alpha α 的值,看看会发生什么:
# initialize parameters
w_init = 0
b_init = 0
# set alpha to a large value
iterations = 10
tmp_alpha = 8.0e-1
# run gradient descent
w_final, b_final, J_hist, p_hist = gradient_descent(x_train ,y_train, w_init, b_init, tmp_alpha,
iterations, compute_cost, compute_gradient)
在上面的例子中, w w w 和 b b b 在正负之间来回反弹,绝对值随着每次迭代而增加。此外,每次迭代 ∂ J ( w , b ) ∂ w \frac{\partial J(w,b)}{\partial w} ∂w∂J(w,b) 都会改变符号,成本增加而不是减少。这清楚地表明 学习率过大,解决方案正在发散。
让我们用一个图来可视化这一点。
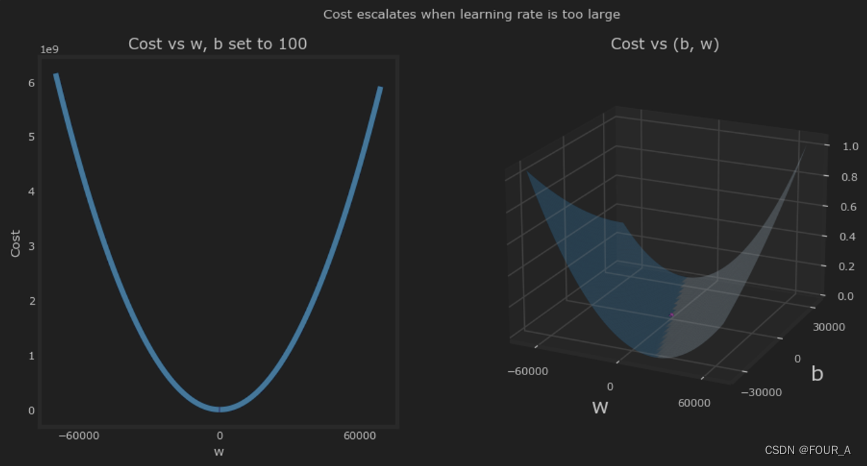
上面,左图显示了梯度下降的前几步中 w w w 的变化。 w w w 在正负之间振荡,成本迅速增长。梯度下降同时作用于 w w w 和 ∗ ∗ b ∗ ∗ **b** ∗∗b∗∗,所以需要右边的 3D 图来完整地展示情况。
总结
在这个实验中,你:
- 深入了解了单变量梯度下降的细节。
- 开发了计算梯度的程序。
- 可视化了梯度是什么。
- 完成了梯度下降例程。
- 利用梯度下降找到了参数。
- 考察了学习率大小对结果的影响。


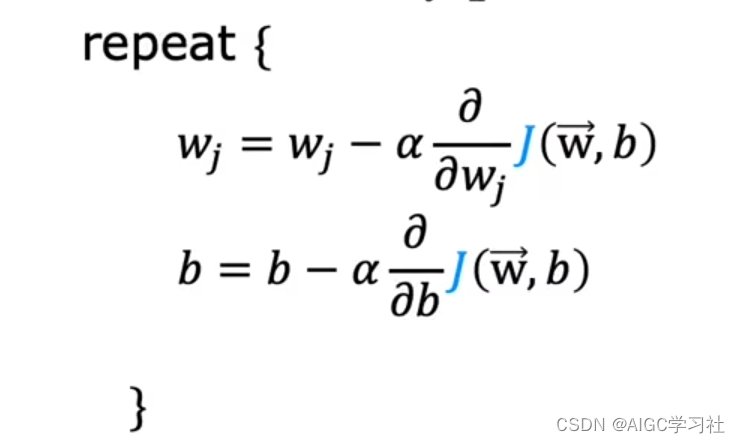


























![[muduo网络库]——muduo库三大核心组件之Channel类(剖析muduo网络库核心部分、设计思想)](https://img-blog.csdnimg.cn/direct/c835e66dd7f3493e94b40369c641205e.png)