基于感知机+全批量梯度下降，实现鸢尾花数据二分类

本文章是笔者在大三时的《模式识别》课程作业，如今将此作业上传供网友学习。

1 感知机的基本原理

1.1概述

感知机（perceptron）是二分类的线性分类模型，属于监督学习算法。输入为实例的特征向量，输出为实例的类别（取+1和-1）。感知机旨在求出将输入空间中的实例划分为两类的分离超平面。为求得超平面，感知机导入了基于误分类的损失函数，利用梯度下降法对损失函数进行最优化求解。

如果训练数据集是线性可分的，则感知机一定能求得分离超平面。如果是非线性可分的数据，则无法获得超平面。

感知机具有简单而易于实现的优点，分为原始形式和对偶形式。感知机预测是用学习得到的感知机模型对新的实例进行预测的,因此属于判别模型。感知机是神经网络和支持向量机的基础。

1.2 感知机模型

假设训练数据集为 $D=\left\{(x_i,y_i) \right\}_{i=1}^{m}$ ,其中, $x_i\in \boldsymbol{X}\subseteq \boldsymbol{R}^n,y_i\in \boldsymbol{Y}=\left\{ +1,-1 \right\}$ 。

感知机模型为： $f(x)=sign(w\cdot y+b)\tag{1}$

其中， $w$ 和 $b$ 称为感知机参数模型， $w\in \boldsymbol{R}^n$ 叫做权值或者权值向量， $b\in \boldsymbol{R}$ 叫做偏置。 $W\cdot x$ 表示 $w$ 和 $x$ 的内积。 $s i g n$ 函数为符号函数：
$=\begin{cases} +1 \qquad x\geqslant 0\\ -1 \qquad x<0\\ \end{cases}\tag{2}$
感知机模型的其中一个超平面是：
${w\cdot x+b=0}\tag{3}$
其中 $w$ 是超平面的法向量， $b$ 是超平面的截距。这个超平面将样本点分为正负两类。即对所有 $y_i=+1$ 的样本，都有 $w\cdot x_i+b>0$ ;对于所有 $y_i=-1$ 的样本，都有 $w\cdot x_i+b<0$ 。

1.3 感知机损失函数

假设训练数据集是线性可分的，为了找出一个能够将训练数据集正实例点和负实例点完全正确分开的超平面，即确定感知机模型参数 $w$ 、 $b$ ，需要确定一个学习策略，即定义（经验）损失函数，并将损失函数极小化。

损失函数的一个自然选择是误分类点的总数，但是这样的函数不是连续可导函数，不易优化。因此感知机采用的损失函数是误分类点到超平面的总距离。
任意一个样本点 $x_i$ 到超平面 $\boldsymbol S$ 的距离为：
$\frac{\left| w\cdot x_i+b \right|}{\left\| w \right\|}$
这里的 $\left\| w \right\|$ 是 $w$ 的 $\boldsymbol L_2$ 范数。
对于误分类的数据 $x_i,y_i)$ 来说， $-y_i(w,x_i+b)=|w\cdot x_i+b|>0$ ,然后假设超平面 $S$ 的误分类点集合为 $M$ ，那么所有误分类点到超平面 $S$ 的总距离为：
$-\frac{1}{\left\| w \right\|}\sum_{x_i\in M}{y_i\left( w\cdot x_i+b \right)}$
不考虑 $-\frac{1}{\left\| w \right\|}$ ,就得到感知机学习的损失函数：
$\boldsymbol L(w,b)=-\sum_{x_i\in M}{y_i\left( w\cdot x_i+b \right)}\tag{4}$

1.4感知机学习算法

1.4.1感知机原始形式与算法描述

至此，感知机学习问题就转化为了求解损失函数的最优化问题。

由于感知机学习算法是误分类驱动的，这里基于随机梯度下降法（SGD）进行优化求解。即任意选取一个超平面 $w_0$ , $b_0$ ，然后用梯度下降法不断地极小化损失函数。极小化过程中不是一次使 $M$ 中的所有误分类点的梯度下降，而是一次随机选取一个误分类点使其梯度下降。

这里不能使用基于所有样本的批量梯度下降（BGD）进行优化。这是因为我们的损失函数里面有限定，只有误分类的 $M$ 集合里面的样本才能参与损失函数的优化。所以我们不能用最普通的批量梯度下降，只能采用随机梯度下降（SGD）或者小批量梯度下降（MBGD）。
损失函数 $L (w, b)$ 的梯度为：
$\begin{cases} \nabla _wL\left( w,b \right) =-\sum_{x_i\in M}{y_ix_i}\\ \nabla _bL\left( w,b \right) =-\sum_{x_i\in M}{y_i}\\ \end{cases}$
随机选取一个误分类点 $x_i,y_i)$ ,对 $w$ , $b$ 进行更新：
$\begin{cases} w\gets w+\eta y_ix_i\\ b\gets b+\eta y_i\\ \end{cases}$
算法描述：

输入：训练数据集为 $D=\left\{(x_i,y_i) \right\}_{i=1}^{m}$ ,其中, $x_i\in \boldsymbol{X}\subseteq \boldsymbol{R}^n,y_i\in \boldsymbol{Y}=\left\{ +1,-1 \right\}$ ；学习率 $\eta( 0<\eta \leqslant 1)$
过程：
$(1)$ 选取初值 $w_0$ , $b_0$ ;
$(2)$ 在训练集中选取数据 $x_i,y_i)$ ;
$(3)$ 判断该数据点是否为当前模型的误分类点，即判断 $y_i(w\cdot x_i+b)\leqslant 0$ ,如果成立则为误分类点，进行更新: $\begin{cases} w\gets w+\eta y_ix_i\\ b\gets b+\eta y_i\\ \end{cases}$
$(4)$ 转到第 $(2)$ 步，直到训练集中没有误分类点。
输出： $w$ 、 $b$ ; 感知机模型： $f(x)=sign(w\cdot y+b)$

1.4.2感知机对偶形式与算法描述

前面介绍了感知机算法的原始形式，下面要介绍的对偶形式是对算法执行速度的优化。

每次梯度的迭代都是选择的一个样本来更新 $w$ 和 $b$ 向量。最终经过若干次的迭代得到最终的结果。对于从来都没有误分类过的样本，它选择参与 $w$ 和 $b$ 迭代修改的次数是0，对于被多次误分类而更新的样本，它参与 $w$ 和 $b$ 迭代修改的次数假设为 $n_i$ 。
则 $w$ 和 $b$ 关于 $x_i,y_i)$ 的增量分别为 $\alpha _i y_ix_i$ 和 $\alpha _iy_i$ ,这里$\alpha _i=n_i\eta $。如果令$ w $和$ b $的向量初始值为 0 向量，这样我们最后学习到的$ w $和$ b$可以分别为：
$\begin{cases} w=\sum\nolimits_{x_i\in M}{\eta y_ix_i}=\sum_{i=1}^{n}{\alpha_i y_ix_i}\\ \nabla _bL\left( w,b \right) =-\sum_{x_i\in M}{y_i}\\ \end{cases}$

这样的话，在每一步判断误分类条件的地方，我们将 $y_i(w\cdot x_i+b)\leqslant 0$ 变种为 $y_i(\sum_{j=1}^{n}{\alpha_j y_jx_j}\cdot x_i+b)\leqslant 0$ 来判断误分类。这个判断误分类的形式里面是计算两个样本 $x_i$ 和 $x_j$ 的内积，而且这个内积计算的结果在下面的迭代次数中可以重用。如果我们事先用矩阵运算计算出所有的样本之间的内积，那么在算法运行时，仅仅一次的矩阵内积运算比多次的循环计算省时。计算量最大的判断误分类这儿就省下了很多的时间，这也是对偶形式的感知机模型比原始形式优的原因。

对偶形式中训练实例仅以内积的形式出现，为了减少计算量，我们可以预先将训练集样本间的内积计算出来，也就是Gram矩阵：
$G=\left[ x_i,x_j \right] _{m\times m}$

算法描述：

输入：训练数据集为 $D=\left\{(x_i,y_i) \right\}_{i=1}^{m}$ ,其中, $x_i\in \boldsymbol{X}\subseteq \boldsymbol{R}^n,y_i\in \boldsymbol{Y}=\left\{ +1,-1 \right\}$ ；学习率 $\eta( 0<\eta \leqslant 1)$
过程：
$(1)$ 选取初值 $\alpha=0$ , $b = 0$ ;
$(2)$ 在训练集中选取数据 $x_i,y_i)$ ;
$(3)$ 判断该数据点是否为当前模型的误分类点，即判断 $y_i(\sum_{j=1}^{n}{\alpha_j y_jx_j}\cdot x_i+b)\leqslant 0$ ,如果成立则为误分类点，进行更新：
$\begin{cases} \alpha_i=\alpha_i +\eta\\ b=b+\eta y_i \end{cases}$
$(4)$ 转到第 $(2)$ 步，直到训练集中没有误分类点。
输出： $\alpha$ 、 $b$ ; 感知机模型： $f(x)=sign(\sum_{j=1}^{n}{\alpha_j y_jx_j}\cdot x_i+b)$

1.4.3原始形式与对偶形式的选择

如果特征数过高，计算内积非常耗时，应选择对偶形式算法加速。
如果样本数过多，每次计算累计和就没有必要，应选择原始算法。

2 梯度下降法

梯度下降法作为机器学习中较常使用的优化算法，其有着3种不同的形式：批量梯度下降（Batch Gradient Descent）、随机梯度下降（Stochastic Gradient Descent）、小批量梯度下降（Mini-Batch Gradient Descent）。其中小批量梯度下降法也常用在深度学习中进行模型的训练。

批量梯度下降(Batch Gradient Descent，BGD)

使用整个训练集的优化算法被称为批量(batch)或确定性(deterministic)梯度算法，因为它们会在一个大批量中同时处理所有样本。全批量梯度下降法是最原始的形式，它是指在每一次迭代时使用所有样本来进行梯度的更新。
2. 随机梯度下降(Stochastic Gradient Descent，SGD)

随机梯度下降法不同于批量梯度下降，随机梯度下降是在每次迭代时使用一个样本来对参数进行更新（mini-batch size =1）。
3. 小批量梯度下降(Mini-batch Gradient Descent，MBGD)

大多数用于深度学习的梯度下降算法介于以上两者之间，使用一个以上而又不是全部的训练样本。传统上，这些会被称为小批量(mini-batch)或小批量随机(mini-batch stochastic)方法，现在通常将它们简单地成为随机(stochastic)方法。对于深度学习模型而言，人们所说的“随机梯度下降, SGD”，其实就是基于小批量（mini-batch）的随机梯度下降。

什么是小批量梯度下降？具体的说：在算法的每一步，我们从具有 $m$ 个样本的训练集(已经打乱样本的顺序)中随机抽出一小批量(mini-batch)样本。小批量的数目 $m^{'}$ 通常是一个相对较小的数(从1到几百)。重要的是，当训练集大小 $m$ 增长时， $m^{'}$ 通常是固定的。我们可能在拟合几十亿的样本时，每次更新计算只用到几百个样本。

3 二分类流程

导入所需库

import csv
import numpy as np
from matplotlib import pyplot as plt
import pylab

读取Iris数据集，并查看部分数据
抽取样本：取前两类样本（共100条），将数据集的4个属性作为自变量X。将数据集的2个类别映射为{-1, 1}，作为因变量Y。

with open('iris.data') as csv_file:
    data = list(csv.reader(csv_file, delimiter=','))
    
label_map = {
    'Iris-setosa': -1,
    'Iris-versicolor': 1,
}

X = np.array([[float(x) for x in s[:-1]] for s in data[:100]], np.float32)
Y = np.array([[label_map[s[-1]]] for s in data[:100]], np.float32)

分割数据集：将数据集按8:2划分为训练集和验证集：

train_idx = np.random.choice(100, 80, replace=False)
test_idx = np.array(list(set(range(100)) - set(train_idx)))
# set函数创建一个无序不重复元素集，可进行关系测试，删除重复数据，还可以计算交集、差集、并集等。
X_train, Y_train = X[train_idx], Y[train_idx]
X_test, Y_test = X[test_idx], Y[test_idx]
# print(X_train)
# print(Y_train)

样本可视化：取样本的前两个属性进行2维可视化，可以看到在前两个属性上两类样本是线性可分的。

plt.figure(figsize=(6, 6))
plt.style.use('seaborn-darkgrid') # 设置画图的风格 
plt.scatter(X[:50, 0], X[:50, 1], label='Iris-setosa') # 前50个数据点为1类
plt.scatter(X[50:, 0], X[50:, 1], label='Iris-versicolor') # 后50个数据点为1类
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

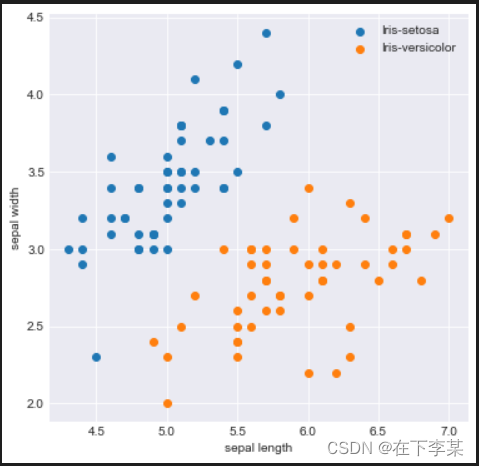
在这里插入图片描述

使用感知机的对偶形式和全批量梯度下降算法完成二分类问题

# 感知机学习类（对偶形式）
class Perception(object):  # 定义 感知机学习类
    def __init__(self, X, Y,TX,TY,epoch,eta):  # X为训练集样本,Y是训练集结果， X为测试集样本,Y是测试集结果,epoch是训练次数,eta是学习率
        if X.shape[0] != Y.shape[0]:  # 要求X,Y中的数目一样
            raise ValueError('Error,X and Y must be same when axis=0 ')
        else:  # 在类中储存参数
            self.X = X
            self.Y = Y
            self.TX = TX
            self.TY = TY
            self.epoch = epoch
            self.eta = eta
            self.len=self.X.shape[0]
            G = np.zeros((X.shape[0],X.shape[0]))#计算内积Gram矩阵
            # G=X.dot(X)
            for i in range(X.shape[0]):
                for j in range(X.shape[0]):
                    G[i,j] = X[i] @ X[j]
            self.G = G
    def ini_test(self,X,Y,a,b):#计算每次训练的正确率
        weight = 0
        for i in range(self.len):  # 循环开始
            weight += a[i]*self.X[i]*self.Y[i]
        num = 0 # 正确分类点个数
        for i in range(len(X)):  # 循环开始
            if Y[i] * (weight @ X[i] + b) > 0:  # 错误判断条件 这里@表示的是矩阵运算的乘法
                num += 1
        return num/(len(X))
      def ini_Per(self):  # 感知机的对偶形式
        a = np.zeros(self.len)  # 初始化a,b
        b = 0
        train_acc=[]     #保存每次迭代的准确率，以画出训练误差随迭代次数产生的曲线
        test_acc= [] 
        for i in range(self.epoch):
            train_acc.append(Perception.ini_test(self,self.X,self.Y,a,b))
            test_acc.append(Perception.ini_test(self,self.TX,self.TY,a,b))
            print('epoch:',i,'Train_acc:',train_acc[-1],'Test_acc',test_acc[-1])
            for j in range(self.len):
                temp=0
                for k in range(self.X.shape[0]):
                    temp += a[k]*self.Y[k]*self.G[k,j]

                if self.Y[j] * (temp + b) <= 0:  # 错误判断条件
                    a[j] += self.eta   # 进行更新a，b
                    b += self.eta * self.Y[j]
        return a, b, train_acc,test_acc  # 返回值

测试验证函数

# 测试验证函数
def test(weight,b,X,Y):
    num = 0 # 正确分类点个数
    for i in range(X.shape[0]):  # 循环开始
        if Y[i] * (weight @ X[i] + b) > 0:  # 错误判断条件 这里@表示的是矩阵运算的乘法
            num += 1
    return num/(X.shape[0])
训练
#使用训练集的两个维度
X_train = X_train[:,0:2]
X_test= X_test[:,0:2]

训练

epoch=500
PER = Perception(X_train, Y_train,X_test,Y_test,epoch, 0.8) # 类初始化
a,b,train_acc,test_acc = PER.ini_Per()
分类结果可视化：
weight = 0
for i in range(X_train.shape[0]):  # 循环开始
    weight += a[i]*X_train[i]*Y_train[i]
# print(accuracy)

输出结果

Output exceeds the size limit. Open the full output data in a text editor
epoch: 0 Train_acc: 0.0 Test_acc 0.0
epoch: 1 Train_acc: 0.9875 Test_acc 1.0
epoch: 2 Train_acc: 0.9625 Test_acc 1.0
epoch: 3 Train_acc: 0.9625 Test_acc 1.0
epoch: 4 Train_acc: 0.9375 Test_acc 0.95
epoch: 5 Train_acc: 0.95 Test_acc 1.0
epoch: 6 Train_acc: 0.925 Test_acc 0.95
epoch: 7 Train_acc: 0.875 Test_acc 0.9
epoch: 8 Train_acc: 0.975 Test_acc 1.0
epoch: 9 Train_acc: 0.9375 Test_acc 0.95
epoch: 10 Train_acc: 0.9375 Test_acc 0.9
epoch: 11 Train_acc: 0.9875 Test_acc 1.0
epoch: 12 Train_acc: 0.9625 Test_acc 1.0
epoch: 13 Train_acc: 0.975 Test_acc 1.0
epoch: 14 Train_acc: 0.9875 Test_acc 1.0
epoch: 15 Train_acc: 0.8375 Test_acc 0.85
epoch: 16 Train_acc: 0.9875 Test_acc 1.0
epoch: 17 Train_acc: 0.9375 Test_acc 0.95
epoch: 18 Train_acc: 0.9875 Test_acc 1.0
epoch: 19 Train_acc: 0.9625 Test_acc 1.0
epoch: 20 Train_acc: 0.975 Test_acc 0.95
epoch: 21 Train_acc: 0.9625 Test_acc 1.0
epoch: 22 Train_acc: 0.975 Test_acc 1.0
epoch: 23 Train_acc: 0.9625 Test_acc 1.0
epoch: 24 Train_acc: 0.9875 Test_acc 1.0
...
epoch: 496 Train_acc: 1.0 Test_acc 1.0
epoch: 497 Train_acc: 1.0 Test_acc 1.0
epoch: 498 Train_acc: 1.0 Test_acc 1.0
epoch: 499 Train_acc: 1.0 Test_acc 1.0

分类结果可视化

plt.figure(figsize=(6, 6))
plt.style.use('seaborn-darkgrid') # 设置画图的风格 
plt.scatter(X[:50, 0], X [:50, 1], label='Iris-setosa') # 前50个数据点为1类
plt.scatter(X[50:, 0], X [50:, 1], label='Iris-versicolor') # 后50个数据点为1类
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()

# 可视化分类平面
x = np.linspace(3, 8, 100)
y = -(weight[0]*x + b)/weight[1]
plt.plot(x, y)

在这里插入图片描述

训练误差和测试误差随着迭代次数改变的变化
print("训练次数",epoch)
plt.figure(figsize=(10, 6))#设置图片大小
plt.style.use('seaborn-darkgrid') # 设置画图的风格 
plt.subplot(1, 2, 1)
plt.ylim((0, 1.1))
plt.plot(train_acc)
plt.xlabel('train times')
plt.ylabel('Train Accuracy')
plt.subplot(1, 2, 2)
plt.ylim((0, 1.1))
plt.plot(test_acc)
plt.xlabel('train times')
plt.ylabel('Test Accuracy')
#最终的测试精度和训练精度
train_acc1 = test(weight,b,X_test,Y_test)
print('Train accuracy is', train_acc1)
test_acc1 = test(weight,b,X_test,Y_test)
print('Test accuracy is', test_acc1)

输出结果：

训练次数 500
Train accuracy is 1.0
Test accuracy is 1.0

在这里插入图片描述

4 实验总结

4.1实验状况说明

因为数据集的前两个维度所表示的数据点中有几个数据之间只具有微小的数据差别，而且该报告所选取的正是数据集的前两个维度1进行二分类，所以这些数据点难以被很好的二分类，因此训练准确性一直在0.975-1之间不停的在波动，测试准确性在0.95-1之间波动，所以最后的train accuracy和test accuracy图像也呈现出波动的现象；
另外在随机选取80个训练集时，如果这些难以被区分的点都在训练集，则测试集准确性将会保持在1。如果这些点都在测试集，则训练集准确性将会保持在1

4.2 实验感悟

对感知机原始形式和对偶形式有了一个初步的认识，对感知机实现二分类问题的算法编程过程有了系统性的理解。
了解道路三种梯度下降算法，明晰了三种算法的具体区别与优缺点(篇幅限制，未写在作业中)，并使用了全批量梯度下降算法实现了二分类问题。
世界上不存在一个完美的算法可以将所有的数据或者现象得到百分之百的完美处理，我们只能不断的改进这些方法以取得最满意的处理效果

5 借鉴博客

[1] 邓坤元 $\quad$ 【机器学习】感知机原理详解 $\quad$ https://blog.csdn.net/pxhdky/article/details/86360535
[2] 明·煜 $\quad$ 作业一 ·感知机实现二分类 $\quad$ https://blog.csdn.net/weixin_53195427/article/details/130180454?spm=1001.2014.3001.5501
[3] G-kdom $\quad$ 批量梯度下降(BGD)、随机梯度下降(SGD)、小批量梯度下降(MBGD) $\quad$ https://zhuanlan.zhihu.com/p/72929546