1.原理
提升方法实际采用加法模型(即基函数的线性组合)与前向分步算法。以决策树为基函数的提升方法称为提升树(boosting tree)。对分类问题决策树是二叉分类树,对回归问题决策树是二叉回归树。提升树模型可以表示为决策树的加法模型:
f M ( x ) = ∑ m = 1 M T ( x ; θ m ) f_M(x)=\sum_{m=1}^MT(x;\theta_m) fM(x)=m=1∑MT(x;θm)
其中, T ( x ; θ m ) T(x;\theta_{m}) T(x;θm)表示决策树, θ m \theta_{m} θm为决策树参数,M为树的个数。
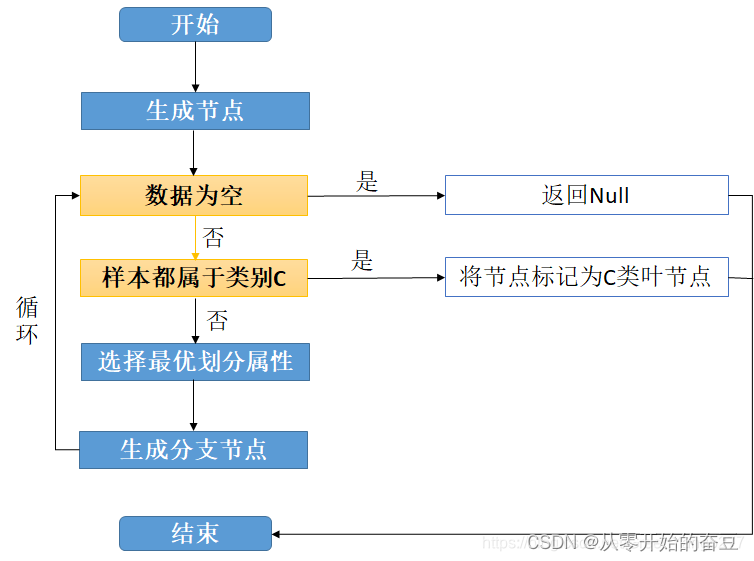
而梯度提升树的具体步骤如下:
1.初始化 f 0 ( x ) = 0 f_{0}(x)=0 f0(x)=0,并选取损失函数 L ( y , f ( x ) ) \mathrm{~L(y,f(x))} L(y,f(x));
2.对于 m = 0 , 1 , ⋯ , M \mathrm{m}=0,1,\cdots,\mathrm{M} m=0,1,⋯,M
(1).计算负梯度:
− g m ( x i ) = − ∂ ( L ( y , f ( x i ) ) ) ∂ f ( x i ) f ( x ) = f m − 1 ( x ) -\mathrm{g_m(x_i)=-\frac{\partial\left(L\bigl(y,f(x_i)\bigr)\right)}{\partial f(x_i)}_{f(x)=f_{m-1}(x)}} −gm(xi)=−∂f(xi)∂(L(y,f(xi)))f(x)=fm−1(x)
(2).以负梯度 − g m ( x i ) -\mathrm{g_{m}(x_{i})} −gm(xi)为预测值,训练一个回归树 T ( x ; θ m ) T(x;\theta_{m}) T(x;θm);
(3).更新 f m ( x ) = f m − 1 ( x ) + ρ T ( x ; θ m ) f_{m}(x)=f_{m-1}(x)+\rho T(x;\theta_{m}) fm(x)=fm−1(x)+ρT(x;θm);
3.经过M次迭代后取得的模型即为
f M ( x ) = ∑ m = 1 M ρ T ( x ; θ m ) f_M(x)=\sum_{m=1}^M\rho T(x;\theta_m) fM(x)=m=1∑MρT(x;θm)
这里的 ρ \rho ρ为学习率,可用来防止过拟合。
此次实验用梯度提升树来实现多分类任务,在这种情况下输出模型经过softmax函数转化为每个类别的置信概率,从而实现分类目标。
2.代码
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.ensemble import GradientBoostingClassifier
# 加载鸢尾花数据集
iris = load_iris()
X = iris.data
y = iris.target
# 划分训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# 创建梯度提升树分类器
clf = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=42)
# 训练模型
clf.fit(X_train, y_train)
# 预测测试集
y_pred = clf.predict(X_test)
# 打印预测结果
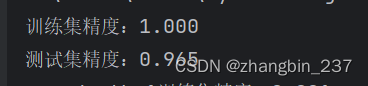
print(y_pred)
我们使用了鸢尾花数据集,这是一个常用的多类别分类数据集。我们首先加载数据,然后划分为训练集和测试集。然后,我们创建一个梯度提升树分类器,并使用训练集对其进行训练。最后,我们使用训练好的模型对测试集进行预测,并打印出预测结果。
GradientBoostingClassifier的参数n_estimators表示弱学习器的最大数量,learning_rate表示学习率,max_depth表示每个弱学习器(决策树)的最大深度,这些参数都可以根据需要进行调整。


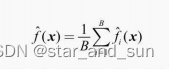






















![[每周一更]-(第41期):深入探索docker的部署方式docker-compose](https://img-blog.csdnimg.cn/direct/ca4985878d4d44fb8af88b4448c2639a.jpeg#pic_center)