引理: ∑ ϵ k ∈ { − 1 , 1 } , 1 ≤ k ≤ n ( ∑ k = 1 n ϵ k a k ) 2 = 2 n ∑ k = 1 n a k 2 \sum_{\epsilon_k\in \{-1,1\},1\le k\le n}(\sum^n_{k=1}\epsilon_ka_k)^2=2^n\sum^n_{k=1}a_k^2 ϵk∈{−1,1},1≤k≤n∑(k=1∑nϵkak)2=2nk=1∑nak2
证明: n = 1 时, L H S = 2 a 1 2 , R H S = 2 a 1 2 ,成立 n=1时,LHS=2a_1^2,RHS=2a_1^2,成立 n=1时,LHS=2a12,RHS=2a12,成立
设 n 时成立,证明 n + 1 时情况: 设n时成立,证明n+1时情况: 设n时成立,证明n+1时情况:
∑ ϵ k ∈ { − 1 , 1 } , 1 ≤ k ≤ n + 1 ( ∑ k = 1 n + 1 ϵ k a k ) 2 \sum_{\epsilon_k\in \{-1,1\},1\le k\le n+1}(\sum^{n+1}_{k=1}\epsilon_ka_k)^2 ϵk∈{−1,1},1≤k≤n+1∑(k=1∑n+1ϵkak)2
= ∑ ϵ k ∈ { − 1 , 1 } , 1 ≤ k ≤ n + 1 ( ( ∑ k = 1 n ϵ k a k ) 2 + 2 ( ∑ k = 1 n ϵ k a k ) ∗ ϵ n + 1 a n + 1 + a n + 1 2 ) =\sum_{\epsilon_k\in \{-1,1\},1\le k\le n+1}((\sum^n_{k=1}\epsilon_ka_k)^2+2(\sum^n_{k=1}\epsilon_ka_k)*\epsilon_{n+1}a_{n+1}+a_{n+1}^2) =ϵk∈{−1,1},1≤k≤n+1∑((k=1∑nϵkak)2+2(k=1∑nϵkak)∗ϵn+1an+1+an+12)
= 2 ∑ ϵ k ∈ { − 1 , 1 } , 1 ≤ k ≤ n + 2 ∑ ϵ n + 1 ∈ { − 1 , 1 } ϵ n + 1 a n + 1 ∑ ϵ k ∈ { − 1 , 1 } , 1 ≤ k ≤ n ϵ k a k + 2 n + 1 × a n + 1 2 =2\sum_{\epsilon_k\in \{-1,1\},1\le k\le n}+2\sum_{\epsilon_{n+1}\in\{-1,1\}}\epsilon_{n+1}a_{n+1}\sum_{\epsilon_k\in \{-1,1\},1\le k\le n}\epsilon_ka_k+2^{n+1}\times a_{n+1}^2 =2ϵk∈{−1,1},1≤k≤n∑+2ϵn+1∈{−1,1}∑ϵn+1an+1ϵk∈{−1,1},1≤k≤n∑ϵkak+2n+1×an+12
= 2 n + 1 ∑ k = 1 n a k 2 + 2 n + 1 × a n + 1 2 = R H S 证毕 =2^{n+1}\sum^n_{k=1}a_k^2+2^{n+1}\times a_{n+1}^2=RHS \ \ \ \ \ \ 证毕 =2n+1k=1∑nak2+2n+1×an+12=RHS 证毕
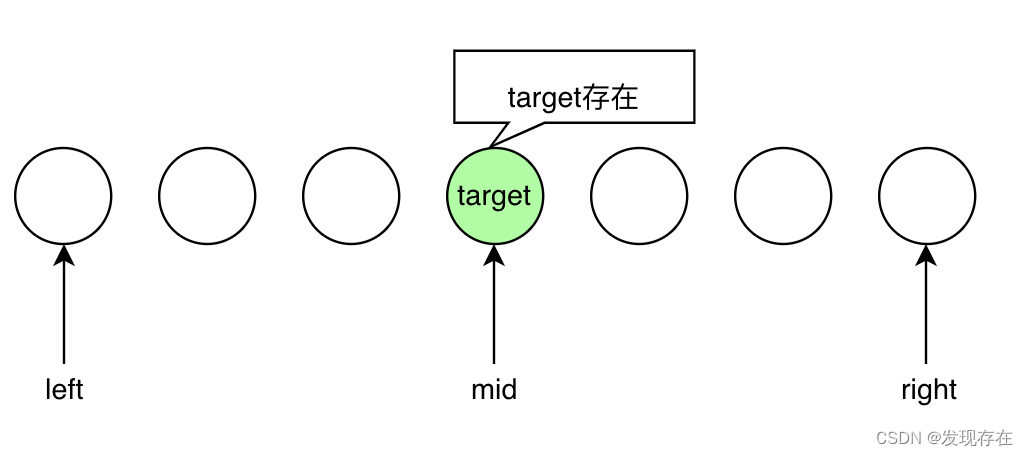
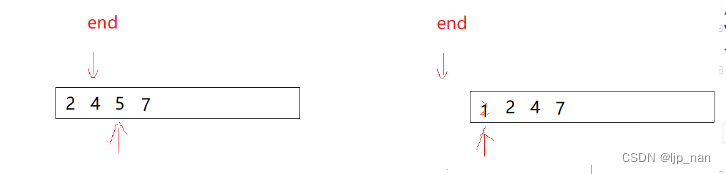
二分搜索边界问题的简单结论
2024-07-20 15:50:02 67 阅读



















![[经验] 眼皮松弛是什么原因导致的 #其他#其他#其他](https://img-home.csdnimg.cn/images/20230724024159.png?origin_url=https%3A%2F%2Fwww.hao123rr.com%2Fzb_users%2Fcache%2Fly_autoimg%2F%25E7%259C%25BC%25E7%259A%25AE%25E6%259D%25BE%25E5%25BC%259B%25E6%2598%25AF%25E4%25BB%2580%25E4%25B9%2588%25E5%258E%259F%25E5%259B%25A0%25E5%25AF%25BC%25E8%2587%25B4%25E7%259A%2584.jpg&pos_id=Rhnkt5t2)