迪杰斯特拉算法
一、算法简介
迪杰斯特拉算法(Dijkstra’s Algorithm)是由荷兰计算机科学家艾茲赫爾·迪克斯特拉(Edsger W. Dijkstra)在1956年提出的一种用于求解图中单源最短路径问题的算法。它适用于带权有向图和无向图,要求图中没有负权重的边。算法的核心思想是通过贪心策略,每次选择距离起点最近的节点进行扩展,逐步找到从起点到所有其他节点的最短路径。
二、算法优势
- 效率高:对于稀疏图,使用二叉堆或斐波那契堆实现的迪杰斯特拉算法具有较高的效率。
- 适用范围广:适用于各种带权图,包括有向图和无向图,只要权重为非负。
- 简单易懂:算法思路清晰,易于理解和实现。
三、算法核心
迪杰斯特拉算法的核心是维护一个优先队列(通常使用最小堆实现),用于存储当前已知最短路径的节点。在算法运行过程中,不断从队列中取出距离起点最近的节点,对其邻接节点进行松弛操作,更新这些节点的最短路径。具体步骤如下:
- 初始化:将起点到起点的距离设置为0,其他所有节点的距离设置为∞,将所有节点放入最小堆中。
- 取堆顶节点:从最小堆中取出距离起点最近的节点,记为当前节点。
- 更新邻接节点:对当前节点的每个邻接节点,检查从起点通过当前节点到该邻接节点的距离是否比当前已知的最短距离更短。如果是,则更新该邻接节点的距离,并将其重新插入最小堆。
- 重复步骤2和3,直到最小堆为空或所有节点都已被访问。
四、算法C++实现
以下是迪杰斯特拉算法的C++实现,使用优先队列来实现最小堆:
#include <iostream>
#include <vector>
#include <queue>
#include <utility>
#include <climits>
using namespace std;
using pii = pair<int, int>;
// 迪杰斯特拉算法实现
vector<int> dijkstra(const vector<vector<pii>>& graph, int start) {
int n = graph.size();
vector<int> dist(n, INT_MAX);
vector<bool> visited(n, false);
dist[start] = 0;
priority_queue<pii, vector<pii>, greater<pii>> pq;
pq.push({ 0, start });
while (!pq.empty()) {
int u = pq.top().second;
pq.pop();
if (visited[u]) continue;
visited[u] = true;
for (const auto& edge : graph[u]) {
int v = edge.first;
int weight = edge.second;
if (dist[u] + weight < dist[v]) {
dist[v] = dist[u] + weight;
pq.push({ dist[v], v });
}
}
}
return dist;
}
int main() {
int n = 5; // 图的节点数
vector<vector<pii>> graph(n);
// 添加边 (节点1, 节点2, 权重)
graph[0].push_back({ 1, 10 });
graph[0].push_back({ 3, 5 });
graph[1].push_back({ 2, 1 });
graph[1].push_back({ 3, 2 });
graph[2].push_back({ 4, 4 });
graph[3].push_back({ 1, 3 });
graph[3].push_back({ 2, 9 });
graph[3].push_back({ 4, 2 });
graph[4].push_back({ 2, 6 });
int start = 0; // 起点
vector<int> distances = dijkstra(graph, start);
for (int i = 0; i < distances.size(); ++i) {
cout << "从节点" << start << " 到节点 " << i << " 的最短路径是 " << distances[i] << endl;
}
return 0;
}

五、代码解释
- 数据结构定义:使用
vector<vector<pii>>来表示图,其中pii是一个pair<int, int>,第一个元素表示邻接节点,第二个元素表示边的权重。 - 初始化:
dist数组用于存储从起点到各个节点的最短距离,初始时设置为INT_MAX(表示无穷大),起点距离自身为0。使用优先队列pq来存储当前已知最短路径的节点。 - 主循环:从优先队列中取出距离起点最近的节点,对其每个邻接节点进行松弛操作,如果通过当前节点到达邻接节点的距离更短,则更新该邻接节点的最短距离,并将其重新插入优先队列。
- 输出结果:最后输出从起点到各个节点的最短距离。
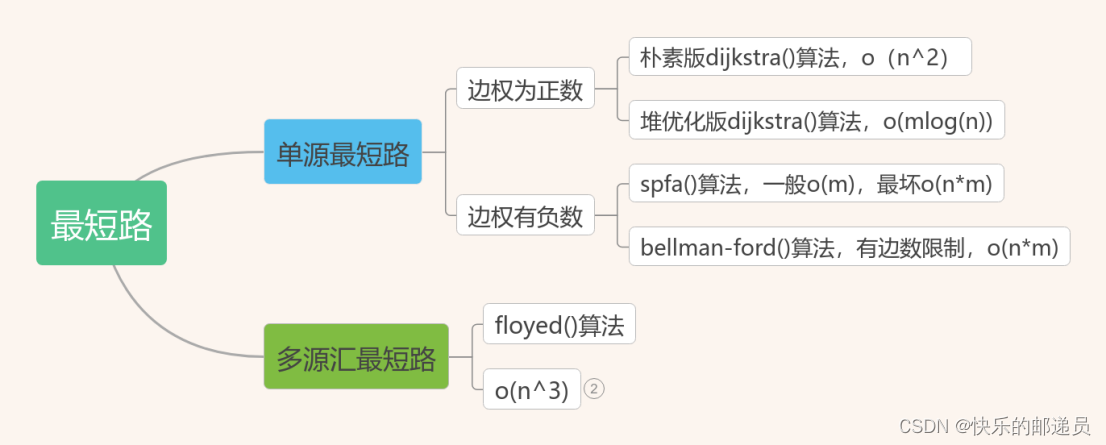
六、数据分析
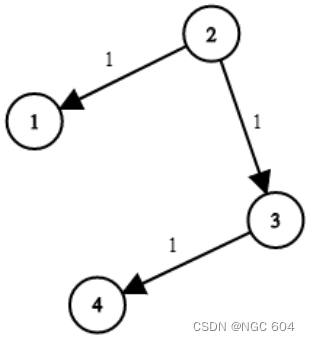
下图为最初的图及其权重

最初的情况是:
1、堆中只有一个数据对 {0,start},表示从start到start的距离最短为0。从这一步开始迭代。
1.1、如果start节点被访问过,那么就回到循环,很显然,start没有被访问过
1.2、遍历可以从start到达的节点,如果从start开始加上权重低于dist中记录过得最小值, 那么更新dist,并且将这一堆添加到堆中。
看一下数据结果
堆的值:{0,0}
dist数组的值 {0,2147483647,2147483647,2147483647,2147483647}
堆的值:{5,3}
dist数组的值 {0,10,2147483647,5,2147483647}
堆的值:{7,4}
dist数组的值 {0,8,14,5,7}
堆的值:{8,1}
dist数组的值 {0,8,13,5,7}
堆的值:{9,2}
dist数组的值 {0,8,9,5,7}
堆的值:{10,1}
dist数组的值 {0,8,9,5,7}
堆的值:{13,2}
dist数组的值 {0,8,9,5,7}
堆的值:{14,2}
dist数组的值 {0,8,9,5,7}
Floyd-Warshall算法
Floyd-Warshall算法是一种用于计算加权图中所有节点间最短路径的算法。它以动态规划的思想,通过逐步增加考虑中间节点,更新所有节点对之间的最短路径。这一算法不仅可以处理有向图,也可以处理无向图,且能处理负权重的边,只要图中不存在负权重的环。
一、算法优势
- 简单直观:算法思路简单,容易理解和实现。
- 全局最优:能够计算出图中所有节点对之间的最短路径,提供全局最优解。
- 适用于负权重:可以处理带有负权重的边,只要没有负权重环。
二、算法核心
Floyd-Warshall算法的核心思想是通过增加中间节点,逐步更新最短路径。具体步骤如下:
- 初始化:创建一个二维数组
dist,其中dist[i][j]表示节点i到节点j的最短距离。初始时,dist[i][j]设置为边(i, j)的权重,如果没有直接的边,则设置为无穷大。 - 动态规划:对每个节点
k,检查通过节点k是否能使节点i到节点j的距离变得更短。如果是,则更新dist[i][j]。 - 重复步骤2,直到所有节点都被考虑为中间节点。
三、算法C++实现
以下是Floyd-Warshall算法的C++实现:
#include <iostream>
#include <vector>
#include <climits>
using namespace std;
// Floyd-Warshall算法实现
void floydWarshall(vector<vector<int>>& graph) {
int n = graph.size();
vector<vector<int>> dist = graph;
for (int k = 0; k < n; ++k) {
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (dist[i][k] != INT_MAX && dist[k][j] != INT_MAX && dist[i][k] + dist[k][j] < dist[i][j]) {
dist[i][j] = dist[i][k] + dist[k][j];
}
}
}
}
// 输出结果
for (int i = 0; i < n; ++i) {
for (int j = 0; j < n; ++j) {
if (dist[i][j] == INT_MAX) {
cout << "INF ";
} else {
cout << dist[i][j] << " ";
}
}
cout << endl;
}
}
int main() {
int n = 4; // 图的节点数
vector<vector<int>> graph = {
{0, 3, INT_MAX, 7},
{8, 0, 2, INT_MAX},
{5, INT_MAX, 0, 1},
{2, INT_MAX, INT_MAX, 0}
};
floydWarshall(graph);
return 0;
}

四、代码解释
- 初始化:
dist数组用于存储节点间的最短距离,初始时设置为graph的权重矩阵。 - 动态规划:三重循环遍历每个节点
k,检查通过节点k是否能使节点i到节点j的距离变得更短。如果是,则更新dist[i][j]。 - 输出结果:最后输出所有节点对之间的最短距离。如果两个节点间没有路径,则输出
INF表示无穷大。
五、结论
Floyd-Warshall算法是一种强大的算法,能够计算图中所有节点对之间的最短路径。它的实现简单,适用于处理负权重的边,但其时间复杂度为O(n^3),因此在处理大规模图时效率较低。
算法的不同
Dijistra是计算一个点到所有点的最短路径,Flody是计算所有点到所有点的最短路径。
Dijistra权值中不能存在负数,Flody中权值可以存在负数。






















![[Spring] Spring Web MVC基础理论](https://i-blog.csdnimg.cn/direct/f0c5b1e3dbe044769fc9fc5c38accbae.jpeg#pic_center)