数据结构（DS）学习笔记（三）：算法和算法分析

参考教材：数据结构C语言版（严蔚敏，吴伟民编著）

工具：XMind、幕布、公式编译器

正在备考，结合自身空闲时间，不定时更新，会在里面加入一些真题帮助理解数据结构

1.2算法与算法分析

1.2.1算法（algorithm）

1.2.2算法的描述

1.2算法与算法分析

1.2.1算法（algorithm）

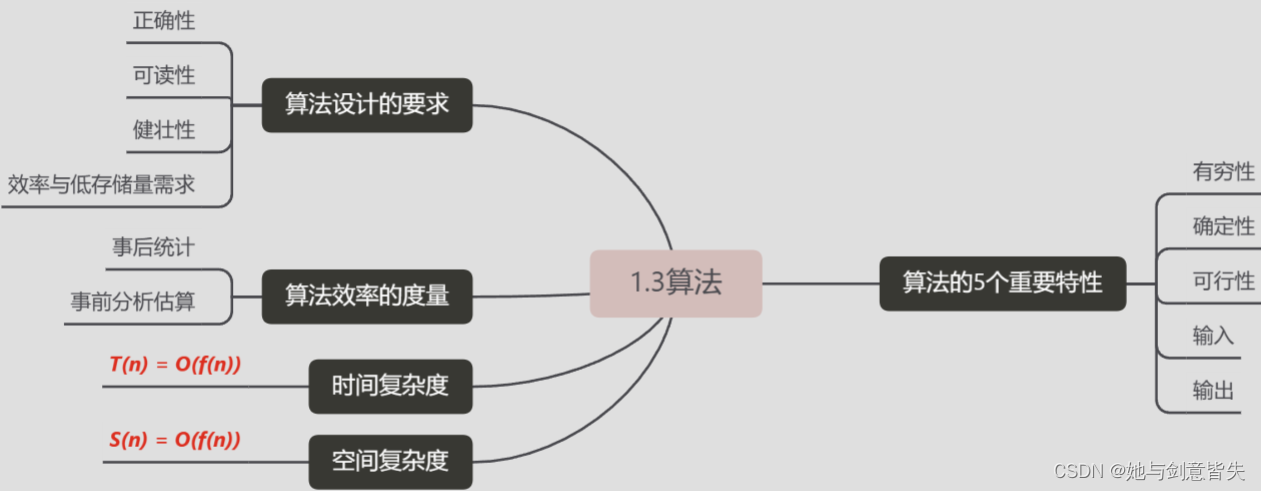
算法：对特定问题求解方法和步骤的一种描述，是指令的有限序列，其中每一条指令表示一个或多个操作。

说白了算法就是解决问题的方法和步骤，第一步要怎么做，第二步要怎么做，第三部要怎么做......
然后列出指令的这样一个序列。
例如：
step1：xxx
step2：xxx
step3：xxx
....    ...

1.2.2算法的描述

自然语言：英文、中文

流程图：传统流程图、NS流程图

伪代码：类语言：类C语言（与C语言类似，但缺少了一些必要的语法细节）

程序代码：C语言程序、Java程序......

举例：

自然语言：

举例：用算法求一元二次方程的根
1.输入方程的系数a、b、c
2.判断a是否等于0，如果等于0，则提示不是一元二次方程；不等于0执行第三步
3.计算△=b²-4ac
4.判断△，如果△=0，计算并输出两个相等实根；如果△＜0，输出没有实根；如果△＞0，输出不等实根
5.结束

传统流程图：

NS流程图：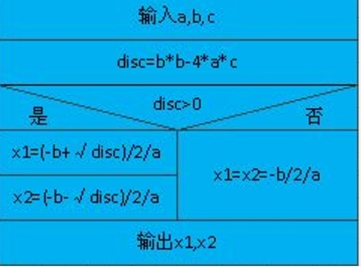

1.2.3算法与程序

算法是解决问题的一种方法或一个过程，考虑如何将输入转换成输出，一个问题可以有多种算法 程序是用某种程序设计语言对算法的具体实现。

程序 = 数据结构 + 算法

数据结构通过算法来实现操作，算法根据数据结构设计程序。

1.2.4算法的5个重要特征

（1）有穷性

一个算法必须总是（对任何合法的输入值）在执行有穷步之后结束，且每一步都可在有穷时间内完成。（算法必须是有穷的，程序可以是无穷的。）

（2）确定性

算法中的每一条指令都必须有确切的含义，无二义性。任何条件下，算法只有唯一的一条执行路径，对于相同的输入只能得出相同的输出。

（3）可行性

一个算法是能行的，可以执行的。算法中描述的操作都可以通过已经实现的基本运算执行有限次来实现的。

（4）输入

一个算法有零个（因为有时候本身自带了输入）或多个的输入，这些输入取自于某个特定的对象的集合。

（5）输出

一个算法有一个或多个的输出，这些输出是同输入有着某些特定关系的量。

1.2.5算法设计的要求

（1）正确性（Correctness）

算法应当满足具体问题的需求。程序对于精心选择的典型、苛刻而带有刁难性的几组输入数据能够得出满足规格说明要求的结果。

（2）可读性（Readability）

可读性好有助于人对算法的理解，算法主要是为了人的阅读与交流，如果算法晦涩难懂，乱七八糟，很难理解，往往会隐藏很多错误，难以调试与修改

（3）健壮性（Robustness）

输出数据非法时，算法也能适当的做出反应或进行处理，而不会产生莫名其妙的输出结果。处理出错的方法，不应该是打印错误信息或异常，并中止程序的执行，而是返回一个表示错误或错误性质的值。

所以，我们要事先预料到可能会出现的问题和错误，事先进行判断，如果有事先处理错误的判断，那么这样的算法就是健壮性好的

（4）效率与低存储量需求（高效率Efficiency）

花尽量少的时间和尽量低的存储需求。

效率：算法执行的时间。 存储量需求：算法执行过程中所需的最大存储空间。

对于同一个问题如果有多个算法可以解决，执行时间短的算法效率高。

一个好的算法首先要具备正确性，然后是健壮性，可读性，在这几个方面都满足的情况下，主要考虑算法的效率，通过算法的效率高低来评判不同算法的优劣程度。

算法的效率：时间效率、空间效率

时间效率：算法所耗的时间 空间效率：算法执行过程中所耗的存储空间

时间效率和空间效率有时是矛盾的

1.2.6算法效率的度量

（一）事后统计（一般不用）

（二）事前分析估算

算法运行时间 = 一个简单操作所需的时间 x 简单操作次数

算法运行时间 = ∑每条语句执行次数 x 该语句执行一次所需的时间

算法运行时间 = ∑每条语句频度 x 该语句执行一次所需的时间

注：1：简单的操作：赋值，移动，比较等。

2：∑：求和符号。

3：每条语句的执行次数也称语句频度。

4：语句执行一次所需的时间是不固定的。与算法无关，取决于机器的指令性能、速度以及编写程序用的语言，不同语言的生成的代码质量不一样，通常高级语言编写的语言，速度更慢。

1.2.7时间复杂度

时间复杂度： $T(n) = O(f(n))$

一般情况下，算法中基本语句重复执行的次数是问题规模n的某个函数f(n)，算法的时间度量记作： $T(n) = O(f(n))$ 。随着问题规模n的增大，算法执行时间的增长率和f(n)的增长率相同，称做算法的渐近时间复杂度，简称时间复杂度。

$T(n)=O(f(n))\Leftrightarrow \lim_{n \to \infty }\frac{T(n)}{f(n)}=k$ （k为常数）

注：1：O表示“同阶”，是数量级符号，当 $n\rightarrow \infty$ 时 $\frac{T(n)}{f(n)}$ 的极限值为不等于零的常数。

        2：n：问题规模 T(n)：时间开销

3：当问题规模n足够大时，可以只考虑阶数高的部分。常数可化为1，可忽略

        例：T(n) = n²+n+5 = O(n²) + O(n) + O(1) = O(n²)

        4：基本语句：执行次数最多的 问题规模n：n越大算法执行时间越长

n：①排序：n为记录数。②矩阵：n为矩阵的阶数，矩阵阶数越大，执行的时间越长。③多项式：n为多项式的项数。④集合：n为元素个数，元素个数越多，处理时间越长。⑤数：n为树的结点个数。⑥图：n为图的顶点数或边数。

5.语句的频度：该语句重复执行的次数 。

定理1：若 $f(n)=a_{m}n^{m}+a_{m-1}n^{m-1}+...+a_{1}n+a_{0}$ 是m次多项式，则 $T(n)=O(m^{n})$ 忽略所有低次幂项和最高次幂系数，体现出增长率的含义，只考虑最高次项（数学中的抓大头）。

1.2.8计算时间复杂度的方法

1.找出语句频度最大的那条语句作为基本语句

2.计算基本语句的频度，得到问题规模n的某个函数f(n)

3.取其数量级用符号"O"表示

例一：用算法表示两个N x N矩阵相乘

for(i=1; i<=n; ++i)    //n+1次
    for(j=1; j<=n; ++j){    //n(n+1)次
        c[i][j] = 0;    //n*n次
        for(k=1; k<=n; ++k)
            c[i][j] += a[i][k] * b[k][j];    //n*n*n次
}

该算法时间消耗为： $T(n)=2n^{3}+3n^{2}+1$ ，当 $n\rightarrow \infty$ 时， $\frac{T(n)}{n^{3}}\rightarrow 2$ ，表示n充分大时，T(n)与n³是同阶或同数量级，引入大“O”记号，则 $T(n) = O(n^{3})$

整个算法的执行时间与该基本操作（乘法）重复执行的次数n³成正比，记 $T(n) = O(n^{3})$

补充：分析以下程序的时间复杂度
for(i=1; i<=n; i++)    
    for(j=1; j<=n; j++){    
        c[i][j] = 0;   
        for(k=1; k<=n; k++)
            c[i][j] = c[i][j] + a[i][k] * b[k][j];    //n*n*n次
}
算法中的基本操作语句为 c[i][j] = c[i][j] + a[i][k] * b[k][j];

$T(n)=O(n^{3})$

级数计算（高数一、三考、数二不考）：首先算 $\sum_{k=1}^{n}1=n$ ，然后算 $\sum_{j=1}^{n}n=n^{2}$ 最后再算 $\sum_{i=1}^{n}n^{2}=n^{3}$ 得 $T(n)=O(n^{3})$

例二：分析以下程序的时间复杂度
for(i=1; i<=n; i++)    
    for(j=1; j<=i; j++) 
        for(k=1; k<=j; k++)
            x = x+1;
$n(n+1)(n+2)=n^{3}+3n^{2}+2n$

最高次是n³，所以 $T(n) = O(n^{3})$

分析：三层嵌套的循环结构。

外层循环 for(i=1; i<=n; i++) 会执行 n 次。

中间层循环 for(j=1; j<=i; j++) 在每一次外层循环迭代中，都会执行 i 次，其中 i 是当前外层循环的迭代变量。因此，随着 i 从 1 增加到 n，中间层循环的总执行次数是 1 + 2 + ... + n = ，这是一个等差数列求和公式，时间复杂度为。

内层循环 for(k=1; k<=j; k++) 在每一次中间层循环迭代中，都会执行 j 次，其中 j 是当前中间层循环的迭代变量。这个循环的执行次数依赖于 j 的值，而 j 的值又依赖于外层循环的变量 i。因此，我们需要对每一层循环进行累加来得到总的操作次数。

为了得到整个算法的时间复杂度，我们需要考虑所有循环的执行次数。最内层循环体（x = x+1;）的执行总次数可以通过累加每一层循环的次数来得到。这相当于计算下面的三重求和： $(\sum_{i=1}^{n} \sum_{j=1}^{i} \sum_{k=1}^{j} 1)$ ,然后算出结果 $T(n) = O(n^{3})$

因为每一项 i*j 对应的 k 循环会执行 j 次，而 j 又依赖于 i，所以最终的操作次数与 n³ 成正比。

例三：分析以下程序的时间复杂度

x = 0; y = 0;
for(int k = 0; k < n; k++)    //for语句本身是n+1次，循环体是n次
    x++;
for(int i = 0; i < n; i++)     //n+1
    for(int j = 0; j < n ; j++)    //(n+1)次,外层每执行一次，他就要执行n(n+1)次
    y++;    //n*n次

$f(n) = n(n+1)\ , T(n) = O(n^{2})$

个人理解分析：

首先这段代码是由两个独立的循环结构，一个是单重循环，另一个是双重循环。

第一个循环：

x = 0; y = 0;
for(int k = 0; k < n; k++)
x++;

这个循环从k=0开始，每次循环k增加1，直到k不再小于n。因此，这个循环会执行n次。在这个循环体内，只有一个简单的操作：x++，这个操作的时间复杂度是O(1)。所以，第一个循环的时间复杂度是O(n)。

第二个循环是一个嵌套循环：
y = 0;
for(int i = 0; i < n; i++)
for(int j = 0; j < n ; j++)
y++;
外层循环从i=0开始，到i=n-1结束，因此会执行n次。对于外层循环的每一次迭代，内层循环都会从j=0开始，到j=n-1结束，执行n次。所以，内层循环总共会执行n*n = n²次。在内层循环体中，只有一个简单的操作y++，这个操作的时间复杂度是O(1)。因此，第二个循环的时间复杂度是O(n²)。

因为整段代码的时间复杂度由复杂度最高的部分决定，即O(n²)。这是因为当n趋于无穷大时，n²的增长速度远大于n，所以O(n²)是整段代码的时间复杂度，意味着随着输入规模n的增大，代码执行所需的时间将大致按照n的平方的速度增长。

例四：分析以下程序的时间复杂度

void exam(float x[ ][ ], int m, int n ){
    float sum [ ];
    for (int i= 0;i< m; i++ ){    //m次
        sum[i]= 0.0;
        for ( int j= 0;j< n;j++ )    //n次
            sum[i] += x[i][j];    //m*n次
    }
    for(i=0;i< m; i++ )
        cout << i <<":"<<sum [i]<< endl;
}

分析：直接找嵌套层次最深的，本体嵌套最深的是：

for (int i= 0;i< m; i++ ){
sum[i]= 0.0;
for ( int j= 0;j< n;j++ )
sum[i] += x[i][j];
}

外层for (int i= 0;i< m; i++ )，从0到m-1，执行m次。内层 for ( intj= 0;j< n;j++ )，从0到n-1，执行n次。外面的循环每执行一次，内部循环就要执行n次，外面循环一共执行了m次，所以总共执行m*n次。所以 $f(n)=m*n \ , T(n)=O(m*n)$

例五：分析以下程序的时间复杂度

i=1;
while(i<=n)
i=i*2;

分析：若循环执行1次:i = 1*2= 2¹, 若循环执行2次:i=2*2= 2² 若循环执行3次:i = 2*2= 2³ 若循环执行x次:i = $2^{x}$

设i = i * 2;执行的次数为x次，由循环条件 i <= n 知，得 $2^{x}\leq n\ ,x\leq log_{2}n$

$2^{f(x)}\leq n\Rightarrow f(n)\leq log_{2}n$ ,取最大值 $f(n)\leq log_{2}n$

所以该程序的时间复杂度为 $T(n)=O(log_{2}n)=O(lg\, n)$

此处lgn：因为不管以谁为底，都可以看做以10为底再乘一个常数，而常数可以忽略

时间复杂度的三种情况：

（一）最好的时间复杂度：1次，元素在第一个位置，即 $T(n)=O(1)$

（二）最坏的时间复杂度：n次，元素在最后一个位置，即 $T(n)=O(n)$

（三）平均的时间复杂度：假设元素n在任意一个位置的概率相同为 $\frac{1}{n}$ ，循环次数： $x=(1+2+3+...+n)*\frac{1}{n}=\frac{n*(n+1)}{2}*\frac{1}{n}=\frac{n+1}{2}$ 即 $T(n)=O(n)$ 平均时间复杂度指在所有可能输入实例在等概率出现的情况下，算法的期望运行时间。

很多算法的执行时间与输入的数据有关，一般总是考虑最坏情况下的时间复杂度，以保证算法的运行时间不会比它更长。

对于复杂的算法，可以拆分为几个简单估算的部分，然后利用大O加法法则和乘法法则，计算算法的时间复杂度：

（一）加法法则：

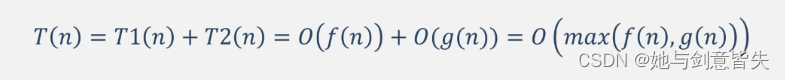
（二）乘法法则：

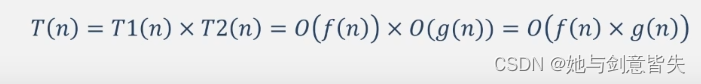
1.2.9算法时间效率的比较

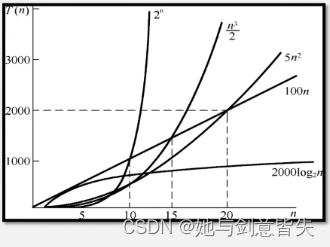
当n取的很大时，指数时间算法多项式时间算法在所需时间上非常悬殊

时间复杂度T(n)按数量递增顺序为：（常对幂指阶）

1.3.0空间复杂度

空间复杂度：算法所需存储空间的量度，记作 $S(n)=O(f(n))$ ,其中n为问题的规模（或大小）

算法的原地工作：算法所需内存空间为常量。（选择题会出）

空间复杂度 = 递归调用的深度

算法要占据的空间：

①算法本身要占据的空间，输入/输出，指令，常数，变量等

②算法要使用的辅助空间

例一：将一维数组a中的n个数逆序存放到原数组中

//算法1
for( i = 0; i < n/2; i++){
    t = a[i];
    a[i] = a[n-i-1];
    a[n-i-1] = t;
}

分析： $\left [ \left | a_{1} \right | \left | a_{2} \right | \left | ... \right |\left | a_{n-1} \right | \left | a_{n} \right | \right ]$ 在一个数组里面存放a1，a2，....，an-1，an，然后逆序， $\left [ \left | a_{n} \right | \left | a_{n-1} \right | \left | ... \right |\left | a_{2} \right | \left | a_{1} \right | \right ]$ 就是将a1和an交换位置，a2和an-1交换位置，一直交换下去，总共有n个元素，所以交换到一半就可以了，也就是n/2次，在交换的时候要有一个临时空间，也就是这里面的t，放入存储元素，用这样的一个临时空间来完成交换，也就是辅助空间。

此处的i是小于n/2的，也就是说取不到n/2，假如是偶数，那么最终i会去到n/2 -1的位置；如果是奇数，i最终会取到n/2向下调整的位置，也就是说会与自己进行交换。

空间复杂度：S(n) = O(1)，也称原地工作（算法有常数阶）

算法1就用了一个变量空间 t = a[i]; 也就是说算法的空间复杂度是1，跟n有多少个元素没有关系，它只需要一个临时变量，所以称它为常数阶

//算法2
for(i = 0; i < n; i++)
    b[i] = a[n-i-1];
for(i = 0; i < n; i++)
    a[i] = b[i];

分析：首先数组的下标是从0开始的，a[i]对应的位序实际上是第i+1个

将a数组的 $\left [ \left | a_{1} \right | \left | a_{2} \right | \left | ... \right |\left | a_{n-1} \right | \left | a_{n} \right | \right ]$ ，按照逆序，放入到b数组 $\left [ \left | a_{n} \right | \left | a_{n-1} \right | \left | ... \right |\left | a_{2} \right | \left | a_{1} \right | \right ]$ 里面。因为a[i] = b[i];，所以再把b数组所有的元素，从下标为0的开始，依次放入a数组中。

算法2需要一个辅助数组b[i]，数组b[i]的大小为：数组a有多大，b就有多大。数组a里面有n个元素，数组b也需要有n个元素，所以它跟元素个数n有关系，即S(n)=O(n)

空间效率为一次阶，n的1次方，跟n 是线性相关的n越多，它需要的辅助空间越多

总结：算法1的空间复杂度（常数的空间算法复杂度）要低于算法2的空间复杂度

空间复杂度：S(n) = O(1) < S(n)=O(n)

算法的空间效率：S(n) = O(1) > S(n)=O(n)