目录
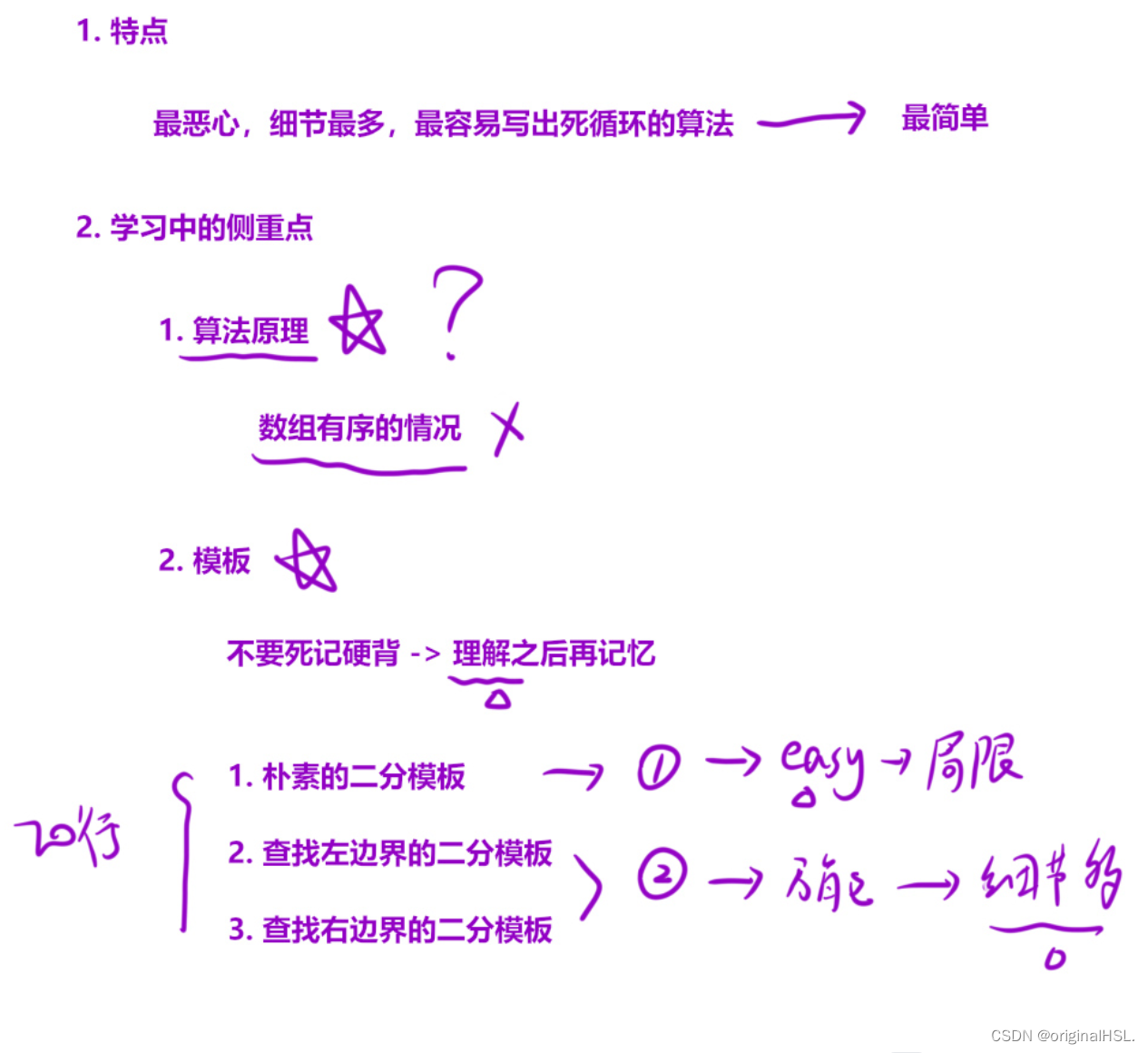
二分查找算法原理
二分查找算法适用于数组有序的情况,当然数组如果无序但是能够找到一个规律,也是可以使用二分查找算法的
二分查找算法模版
这里的模块需要理解之后再记忆
有三个模版,分别是:
①朴素的二分模版
②查找左边界的二分模版
③查找右边界的二分模版
题目一:二分查找
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9输出: 4
解释: 9 出现在 nums中并且下标为 4
示例 2:
输入: nums= [-1,0,3,5,9,12], target = 2输出: -1
解释: 2 不存在 nums中因此返回 -1
解法一:暴力解法
初看这个题,可以很容易想到暴力解法,也就是遍历一遍这个数组,直到找到这个目标值target,返回该目标值的下标即可,若没有找到该目标值,就返回-1即可
暴力解法时间复杂度是O(N)
解法二:二分查找算法
二分查找算法是当数组有二段性的时候,就能够使用二分查找算法了,因为在暴力解法中,依次遍历一次只能排除一个数,而如果数组有二段性,二分查找算法就可以依次排除一块区域的数,因此效率比较高
二段性就是我们所发现一个规律,根据这个规律选取一个点之后(一般选取中间的点),能够将数字分成两部分,根据规律能舍去其中一部分,进而在另一个部分里面继续查找的时候,此时就可以使用二分查找算法了
下面具体讲解二分查找算法:
有一个数组,左端点下标为left,右端点下标为right,中间位置的下标为mid,此时要查找的目标值是t,数组的中间值为x
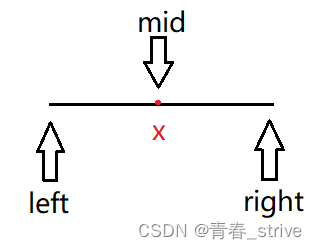
此时选取中间的点x,与目标值t比较会有三种情况:
①x < t :left = mid +1,接着在 [ left, right ]的区间查找
②x > t :right = mid - 1,接着在 [ left, right ]的区间查找
③x == t:返回结果mid
循环的条件:left > right时就停止,因为每次判断完,如果没有找到结果,要不就是right左移或left右移,直到移动结束后left > right,就说明遍历结束了
二分查找算法的时间复杂度是O(logN)
代码如下:
class Solution {
public:
int search(vector<int>& nums, int target)
{
int left = 0, right = nums.size() - 1;
while(left <= right)
{
int mid = left + (right - left) / 2; //防止溢出的风险
if(nums[mid] < target) left = mid + 1;
else if(nums[mid] > target) right = mid - 1;
else return mid;
}
return -1;
}
};有个细节,在算中间值的下标mid时,没有采用(left + right) / 2来计算,因为这种计算方式有可能会导致溢出的风险,因为如果left和right都是极大的数,这两个数相加就可能会导致溢出
因此在这里采用(right - left) / 2,计算出left和right之间的距离的一半,再与left相加,就不会有上述风险了
朴素的二分模版
while(left <= right)
{
int mid = left + (right - left) / 2;
if(......)
left = mid + 1;
else if(......)
right = mid - 1;
else
return ......;
}题目二:在排序数组中查找元素的第⼀个和最后⼀个位置
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8 输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6 输出:[-1,-1]
示例 3:
输入:nums = [], target = 0 输出:[-1,-1]
解法一:暴力解法
同样在遇到这个题时,最容易想到的就是暴力解法了,依旧是遍历数组,在找到的第一个位置处做标记,在找到的最后一个位置处做标记,最后返回,如果没有找到要求的数,就返回[-1, -1]
暴力查找的时间复杂度依旧是O(N)
解法二:朴素二分
这个朴素二分的方法,在这道题中,就明显不太适用了,因为如果一个数组全部是同一个数,那么我使用朴素二分,从中间去一个点,并不能确定剩下符合条件的数是在左边还是右边,所以还是需要向左和右继续找,这样的时间复杂度和暴力解法并没有区别
所以下面详细说明一下查找区间的左端点和右端点的情况:
查找区间左端点
有一个数组如下所示,目标值t等于3,此时需要查找区间的左端点,也就是第一个3出现的位置

所以需要利用二段性, 将数组划分为上图所示的两部分,小于t和大于等于t这两部分
有一个数组,左端点下标为left,右端点下标为right,中间位置的下标为mid,此时要查找的目标值是t,数组的中间值为x

与朴素的二分模版不同,此题的target可能不止一个数,所以中间值与目标值t的比较就有如下两种情况:
①x < t:left = mid + 1,接着在 [ left, right ]的区间查找
②x >= t:right = mid,接着在 [ left, right ]的区间查找
需要注意,当x < t时,因为此时mid所指向的x都是不满足题意的,所以left需要移动到mid的右边,所以是 left = mid + 1
而当 x >= t时,此时的x有可能是目标值,所以right不能像二分的朴素模版那样,移动到mid的左边,而是移动到mid的位置
下面详细说明二分的两个细节:循环条件和求中点的操作
循环条件的相关细节:
关于循环条件:这里选的是 left < right 就进入循环,而不是left <= right
分下面三种情况讨论,来说明为什么循环条件选择 left < right
①数组中有结果:
数组如下,最终结果在ret这个位置开始:
最开始的时候,left是处于不合法的区间,而right是处于合法的区间,left区间和right区间如下所示: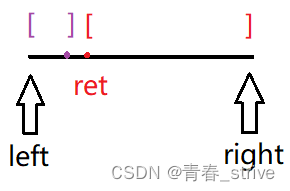
right一直在合法区间上移动的时候,是绝对不会超过ret这个点的,因为right永远执行的是right = mid这个操作
而left是永远想跳出这个不合法区域的,因为left永远执行的是 left = mid + 1这个操作
而当left跳出区域与right相遇后,所指的这个位置正好是最终结果
所以当left = right的时候,就是最终结果了,无需继续判断
②数组全大于t:
如果全是大于t的,那么right是只会向左移动,直到移动到left的位置为止,因为这种情况下,left永远都不会移动,只有right不停地执行right = mid这个操作
此时left和right相遇了,但是这种情况下是没有最终结果的,所以只需判断一下相遇位置的值是否等于t即可,如果相等就返回这个位置的值,如果不相等就返回[-1, -1]即可
所以当left = right的时候,只需再与t比较一次判断是否是左端点的值即可,无需继续进入循环判断
③数组全小于t:
如果全是小于t的,那么left是只会向右移动,直到移动到right的位置为止
当他们相遇时,同样只需判断一下相遇位置的值是否等于t即可
所以当left = right的时候,只需再与t比较一次判断是否是左端点的值即可,无需继续进入循环判断
通过上述的三种情况,证明了循环条件是 left < right,不需要=,因为相等的时候就已经得出最终结果了,没有必要再进入循环中判断了
如果我们的循环条件不是 left < right,而是写成了 left <= right,就会出现死循环的情况
因为如果是第一种情况,left和right都指向了ret的位置,此时继续判断,right依旧是指向该位置,并不发生改变,继续进入循环......从而导致死循环
求中点的操作的相关细节:
在第一题中使用的朴素的二分模版,求中点时,采用的公式是:mid = left + (right - left) / 2
其实还有一个公式也可以求中点:mid = left + (right - left + 1) / 2
区别就是在括号中 +1,那么这两个的区别是什么呢?
很简单,当数组个数是偶数时,例如共有6个数,第一种公式求出来是下图这个位置:
mid = 0 + (5 - 0) / 2 = 2
如果是第二种公式,求出来则是这个位置:
mid = 0 + (5 - 0 + 1) / 2 = 3
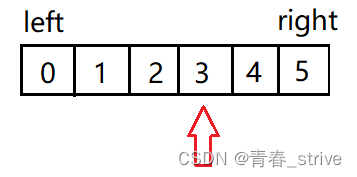
可以观察到,在数组个数是偶数时,中间位置是两块,第一个公式指向的是偏左的那一块位置,而第二个公式指向的则是偏右的那一块位置
这两种情况再朴素二分中都可以使用,而在这种情况下则会有问题
当最后一个left和right指向下图所示的情况时: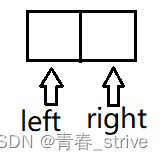
如果采用第二个公式,计算出来mid指向中间偏右的位置,即:
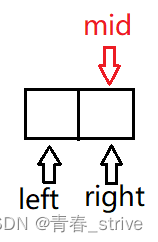
如果是x < t,那么left = mid + 1,此时再判断不满足循环条件left < right,循环就会终止
而如果是x >= t,那么right = mid,此时mid和right指向同一块位置,这时就会出现死循环的情况
因此得出结论,在求区间左端点时,使用第二个公式求中点,就会陷入死循环
而如果采用第一个公式计算中点,mid就会指向: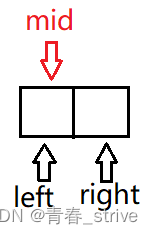
如果是x < t,那么left = mid + 1,此时left和right相遇,循环终止
而如果是x >= t,那么right = mid,此时left和right同样相遇,循环终止
不会出现上述死循环的情况
查找区间右端点
同样是该数组如下所示,目标值t等于3,此时需要查找区间的右端点,也就是最后一个3出现的位置:
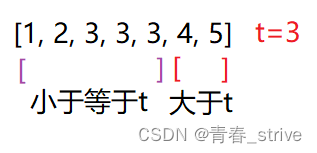
所以需要利用二段性, 将数组划分为上图所示的两部分,小于等于t和大于t这两部分
有一个数组,左端点下标为left,右端点下标为right,中间位置的下标为mid,此时要查找的目标值是t,数组的中间值为x

①x <= t:left = mid,接着在 [ left, right ]的区间查找
②x > t:right = mid - 1,接着在 [ left, right ]的区间查找
当x <= t时,表示结果就在mid的左边这个区域,此时的x有可能是目标值,所以left不能像二分的朴素模版那样,移动到mid的右边,而是移动到mid的位置
当x > t时,因为此时mid所指向的x都是不满足题意的,所以right需要移动到mid的左边,所以是 right= mid + -1
下面详细说明二分的两个细节:循环条件和求中点的操作
循环条件的相关细节:
循环条件同样是left < right
具体证明和上面求左端点的步骤一样,以此类推
求中点的操作的相关细节
求中点的方式依旧是这两个公式
①mid = left + (right - left) / 2
②mid = left + (right - left + 1) / 2
第一个公式求的是靠左的,第二个公式求的是靠右的
当最后一个left和right指向下图所示的情况时:
如果采用第一个公式,计算出来mid指向中间偏左的位置,即:

如果是x <= t,那么left = mid,此时mid和right指向同一块位置,这时就会出现死循环的情况
因此得出结论,在求区间右端点时,使用第一个公式求中点,就会陷入死循环
而如果采用第二个公式计算中点,mid就会指向中间偏右的位置:

如果是x <= t,那么left = mid,此时left和right相遇,循环终止
而如果是x > t,那么right = mid - 1,此时left和right同样相遇,循环终止
不会出现上述死循环的情况
利用上述讲解的计算左端点和右端点的方法,解决此题:
代码如下:
class Solution {
public:
vector<int> searchRange(vector<int>& nums, int target) {
if(nums.size() == 0) return {-1,-1}; //判断边界条件
int left = 0, right = nums.size()-1,begin = 0;
while(left < right) //计算左端点
{
int mid = left + (right -left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
//判断是否有结果
if(nums[left] != target) return {-1,-1};
else begin = left; //begin存储左端点的下标
left = 0, right = nums.size()-1;
while(left < right) //计算右端点
{
int mid = left + (right -left + 1) / 2;
if(nums[mid] <= target) left = mid;
else right = mid - 1;
}
return {begin,right};
}
};查找区间左端点二分模版
while(left < right)
{
int mid = left + (right -left) / 2;
if(......) left = mid + 1;
else right = mid;
}查找区间右端点二分模版
while(left < right)
{
int mid = left + (right -left + 1) / 2;
if(......) left = mid;
else right = mid - 1;
}题目三:搜索插入位置
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5 输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2 输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7 输出: 4
这道题也可以很容易的看出这个数组的二段性
也就是所插入的值要不和数组中的数相等, 要不就是第一次出现比它大的这个数的位置,所以可以得到结论:最终找到的位置应该是大于等于目标值target的
所以利用二段性分为小于target,和大于等于目标值target
代码如下:
class Solution {
public:
int searchInsert(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
if(nums[right] < target) return nums.size(); // 判断边界条件
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] < target) left = mid + 1;
else right = mid;
}
return left;
}
};题目四:x的平方根
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4 输出:2
示例 2:
输入:x = 8 输出:2 解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
解法一:暴力解法
依次列举1、2、3、4、5....的平方,与x做比较,如果比x小就继续往后试,直到找到这个数的平方要么是大于这个数,要么是等于这个数位置,就说明找到了最终解
当等于时就返回这个数,当是大于时就返回它前一个数
解法二:二分查找
二分查找最重要的就是找到二段性
我们可以发现,整个数组可以分为小于等于x和大于x这两个区域
所以就有两种情况:
①mid * mid <= x:left = mid
②mid * mid > x:right = mid - 1
分情况讨论即可
代码如下:
class Solution {
public:
int mySqrt(int x) {
if(x < 1) return 0; // 处理边界条件
long long left = 1, right = x;
while(left < right)
{
long long mid = left + (right - left + 1) / 2;//防溢出
if(mid * mid <= x) left = mid;
else right = mid - 1;
}
return left;
}
};题目五:山峰数组的峰顶
符合下列属性的数组 arr 称为 山脉数组 :
arr.length >= 3- 存在
i(0 < i < arr.length - 1)使得:arr[0] < arr[1] < ... arr[i-1] < arr[i]arr[i] > arr[i+1] > ... > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < ... arr[i - 1] < arr[i] > arr[i + 1] > ... > arr[arr.length - 1] 的下标 i 。
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
示例 1:
输入:arr = [0,1,0] 输出:1
示例 2:
输入:arr = [0,2,1,0] 输出:1
示例 3:
输入:arr = [0,10,5,2] 输出:1
这个题目也是比较好理解的,所给的数组元素的大小,都是先上升再下降的,都存在一个最大值,求这个最大值的下标
解法一:暴力枚举
从前往后依次枚举,当枚举到一个数的值是大于前一个数的,这个数就是峰值,返回下标即可
暴力解法的时间复杂度是O(N)
解法二:二分查找算法
此时根据这个峰值数组的特性,可以找到这个数组的二段性, 如下图所示:
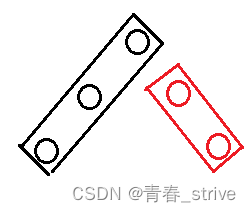
左边的区间包含峰值,每一个数都大于前一个数
右边区域不包含峰值,每一个数都小于小于前一个数
代码如下:
class Solution {
public:
int peakIndexInMountainArray(vector<int>& arr) {
int left = 0, right = arr.size()-1;
while(left < right)
{
int mid = left + (right - left + 1) / 2;
if(arr[mid] > arr[mid-1]) left = mid;
else right = mid - 1;
}
return left;
}
};题目六:寻找峰值
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1] 输出:2 解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4] 输出:1 或 5 解释:你的函数可以返回索引 1,其峰值元素为 2; 或者返回索引 5, 其峰值元素为 6。
这道题需要注意的是:nums[-1] = nums[n] = -∞ 这个条件
表示默认第一个元素前和最后一个元素之后都是最小的,所以如果是如下这种情况,最后一个位置也是峰值,如下:
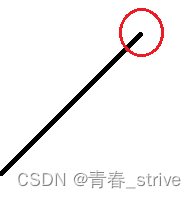
或是这种情况,第一个也是峰值:

这就是刚买这个条件所表达的意思
解法一:暴力枚举
从第一个位置开始暴力枚举,分下面的情况讨论即可:
①第二个数比第一个小,此时第一个数就是峰值
②在走的过程中一直上升,直到遇到一个比该值小的,此时该值就是峰值
③从第一个数开始一直上升,直到最后一个数为止,此时最后一个数是峰值
暴力枚举的时间复杂度是O(N)
解法二:二分查找算法
在arr数组中,有两种情况,一个坐标是i另一个坐标是i+1
如果arr[i] > arr[i+1],说明此时是下降趋势,也就是说答案就在 <= i的区域,此时需要改变right的值
如果arr[i] < arr[i+1],说明此时是上升趋势,也就是说答案就在 > i的区域,此时需要改变left的值
将上述所说的i替换为mid,就可以使用二分查找算法进行计算了
代码如下:
class Solution {
public:
int findPeakElement(vector<int>& nums) {
int left = 0, right = nums.size()-1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > nums[mid + 1]) right = mid;
else left = mid + 1;
}
return left;
}
};题目七:搜索旋转排序数组中的最小值
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转
4次,则可以得到[4,5,6,7,0,1,2] - 若旋转
7次,则可以得到[0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2] 输出:1 解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2] 输出:0 解释:原数组为 [0,1,2,4,5,6,7] ,旋转 3 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17] 输出:11 解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
需要注意数组中的数是互不相同的,需要找出最小元素
解法一:暴力枚举
暴力枚举,遍历一遍数组,找出最小的元素
时间复杂度O(N)
解法二:二分查找算法
此题也可以找到数组的二段性,每一个数组都大致可以分为下面这种情况,即原本的递增数字旋转后,会出现先递增,再递增的趋势:
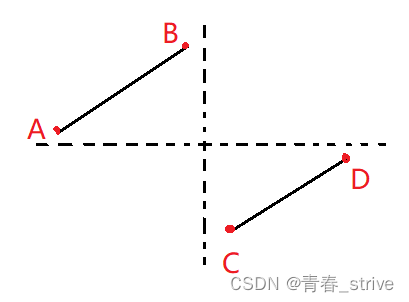
AB这一段都大于D点,CD这一段都小于等于D点,就有了二分查找算法所需的二段性
设D点为x,分为下面两种情况:
①arr[mid] > x,表示在AB线段上,此时改变需要改变左区间
②arr[mid] <= x,表示在CD线段上,此时改变需要改变右区间
代码如下:
class Solution {
public:
int findMin(vector<int>& nums) {
int left = 0, right = nums.size()-1;
int x = nums[right];
while(left < right)
{
int mid = left + (right - left) / 2;
if(nums[mid] > x) left = mid + 1;
else right = mid;
}
return nums[left];
}
};题目八:0〜n-1中缺失的数字
某班级 n 位同学的学号为 0 ~ n-1。点名结果记录于升序数组 records。假定仅有一位同学缺席,请返回他的学号。
示例 1:
输入: records = [0,1,2,3,5] 输出: 4
示例 2:
输入: records = [0, 1, 2, 3, 4, 5, 6, 8] 输出: 7
这里的最后一道题,其实是很简单的,其中是有非常多的解法的,具体如下:
前四种的时间复杂度都是O(N),因为都需要遍历一遍数组
解法一:遍历数组
因为是学号从0开始递增的,所以直接遍历数组,看哪个数断开了
代码如下:
class Solution {
public:
int takeAttendance(vector<int>& records) {
int i = 0;
for (i = 0; i < records.size(); i++)
{
if (records[i] != i)
break;
}
return i;
}
};解法二:哈希表
建立大小为n的哈希表,遍历原始数组,填进哈希表中,接着遍历哈希表,发现哪个数字没有填,答案就是那个数字
class Solution {
public:
int takeAttendance(vector<int>& records) {
int i = 0;
unordered_map<int, int> ump;
for (auto& it : records) ump[it]++;
for (i = 0; i < records.size(); i++)
{
if(!ump.count(i)) break;
}
return i;
}
};用数组替代哈希表:
class Solution {
public:
int takeAttendance(vector<int>& records) {
int i = 0;
int hash[10000] = {0};
for (auto& it : records) hash[it]++;
for (i = 0; i < records.size(); i++)
{
if(hash[i] == 0)
break;
}
return i;
}
};解法三:位运算(异或运算)
异或运算时有个特点:相同为0,相异为1,所以我们可以先把数组中的元素异或一遍,再异或n个递增的数组,异或完后剩下来的就是缺失的数
因为缺失了一个数,所以for循环中个数需要加1
代码如下:
class Solution {
public:
int takeAttendance(vector<int>& records) {
int i = 0, res = 0;
for (auto& it : records) res ^= it;
for (i = 0; i < records.size()+1; i++) res ^= i;
return res;
}
};解法四:数学(高斯求和公式)
也就是将n个数加起来,依次减去原数组中的数,剩下的就是缺失的数
因为n个数从0开始递增,所以公差是1,可以使用(首项 + 末项) * 项数 / 2计算
因为从0开始,共有n个数,所以首项是0,末项是records.size()也就是n,因为假设有3个数,末项是2,而records中缺少了一个数,records.size()就为2,所以可以将records.size()当做末项
项数是n+1,因为n是records.size(),而records缺少了一个数,所以项数需要+1
代码如下:
class Solution {
public:
int takeAttendance(vector<int>& records) {
int i = 0, res = 0, n = records.size();
res = (0 + n)*(n + 1)/2;
for (i = 0; i < records.size(); i++) res -= records[i];
return res;
}
};解法五:二分查找算法
这道题光看数字可能看不出来怎么使用二分,而如果将下标都标注出来, 此时就可以很清晰的看出二段性了,假设数组是0,1,2,3,5,如下所示,黑色的表示数字元素,红色的表示下标:
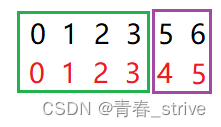
可以很清晰的看到,绿框中元素与所对应的下标是相等的,而紫框中的元素与下标是不同的,这里就体现了二段性,我们要找的就是下标为4的这个位置
①arr[mid] == mid,表示此时在绿框中,需要改变left,即left = mid + 1
②arr[mid] != mid,表示此时在紫框中,需要改变right,并且mid可能是答案,所以right = mid
需要注意边界情况,如果数组是0,1,2,3,4这样的类型,缺了一个5,此时我们按照上述的情况使用二分查找算法,会使得最终的left指向4这个值的下标,所以我们需要最后比较一下,left所对应的值和left是否相等, 如果相等就表示是这种特殊情况,需要进行特殊处理
代码如下:
class Solution {
public:
int takeAttendance(vector<int>& records) {
int left = 0,right = records.size()-1;
while(left < right)
{
int mid = left + (right - left) / 2;
if(records[mid] == mid) left = mid + 1;
else right = mid;
}
//处理细节
return records[left] == left ? left + 1 : left;
}
};二分查找题目到此结束