数的范围---二分法一次搞懂

1. 什么是二分法？

二分法(Bisection method)，即一分为二的的方法。对于在区间[a,b]上连续不断且满足f(a)*f(b)<0的函数y=f(x),通过不断地把函数f(x)的零点所在区间二等分，使区间两个端点逐步逼近零点，进而得到零点的近似值的方法。

说人话：把答案所在的区间逐渐缩小，直到区间内只有答案。

比如猜数字游戏：给定一个1–100之间的正整数，让你猜。猜的过程中给出大小判断的提醒，问怎么才能快速地猜出来？
最快的方法是：每次猜区间的中间点的数字。如果中间点大于给定数字，下次就猜前半部分的中间点数字；如果中间点数字小于给定数字，下次就猜后半部分的中间点数字。

例如：给定56。

1.第一次猜1到100中心的数字：(1+100)/2 = 50,小于给定数字。

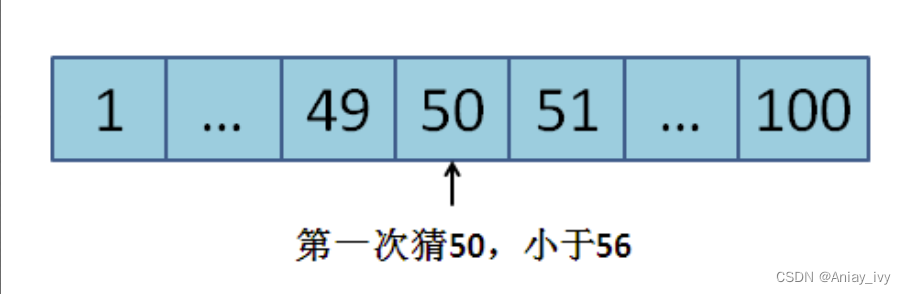
2.第二次猜51到100中心的数字：(51+100)/2 = 75,大于给定数字。

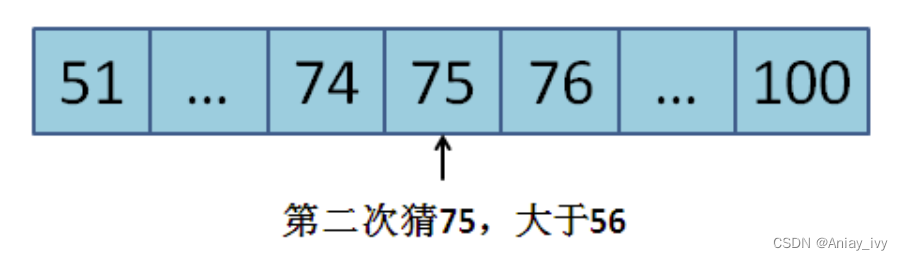
3.第三次猜51到74中心的数字:（51+74)/2 = 62,大于给定数字。

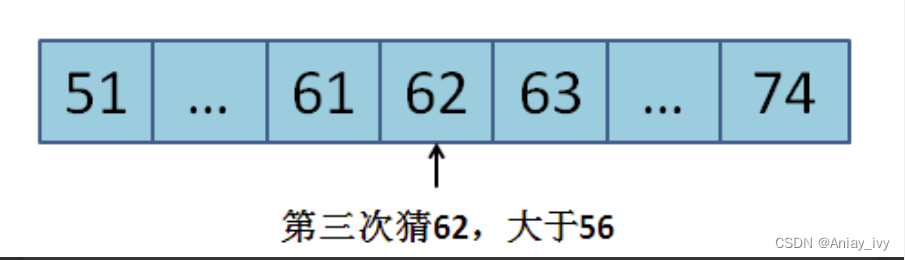
4.第四次猜51到62中心的数字：(51+62)/2 = 56。等于给定数字。

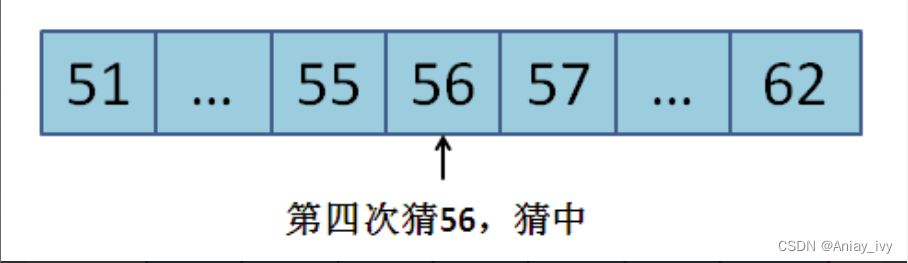
5.结束。
代码：

int main(){
    int l = 1, r = 100;//l表示猜数区间的左端点，r表示猜数区间的右端点
    int target = 56;//给定的数字
    while (l < r)
    {
        int mid = (l + r) / 2;//计算中间点mid的值
        if (mid > target)//中间点的值大于给定数字，往左半部分往左部分猜
            r = mid - 1;//mid 及 mid右侧数字都大于targ，所以r = mid - 1
        else if (mid == target) //mid等于给定数字
        {
            cout << "猜到了，给定数字是：" << mid;
            break;
        }
        else
            l = mid + 1;//中间点的值小于于给定数字，往右半部分往左部分猜
    }
}

2. 如何优雅的处理边界条件？

2.1 左边界、右边界的更新

先看一个例子：给定一个排好序的整数数组a，数组中可能存在重复元素。给定数组中的一个值target，求出它最后出现的位置。
​ 例如数组a为：[1 3 3 3 5],目标值target = 3。a中最后一个等于3的元素为：a[3],所以结果为3。
​ 最容易想到的解决方法是遍历数组，找出target最后出现的位置即可。时间复杂度是O(n)。
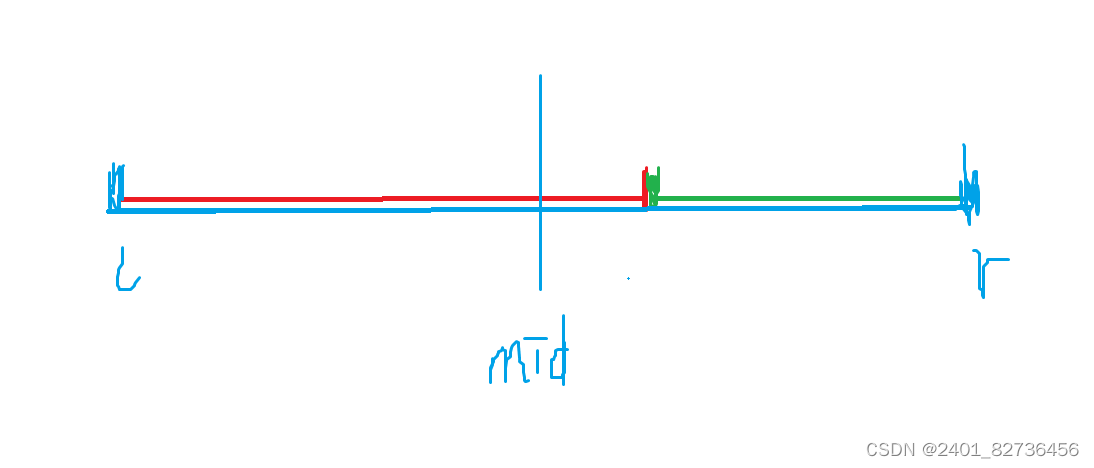
​ 考虑使用二分法：用l指向区间的左端点，r指向区间的右端点，取mid = (l + r) / 2，mid 指向区间中间位置。左右端点更细规则如下：

1. 如果a[mid] > target，target最后一次出现的位置一定在a[mid]之前，更新r：r = mid - 1。
2. 如果a[mid] <= target，target最后一次出现的位置可能在mid处，也可能在a[mid]之后，更新l：l = mid。
3. 直到 l = r时，区间内只有一个元素，这个元素就是target最后一次出现的位置。

看起来很正确的方法，手动模拟下：

第一次：l = 0, r = 4, mid = (l + r) / 2 = 2。a[mid] = 3。符合更新规则2，l更新为mid：l = 2。

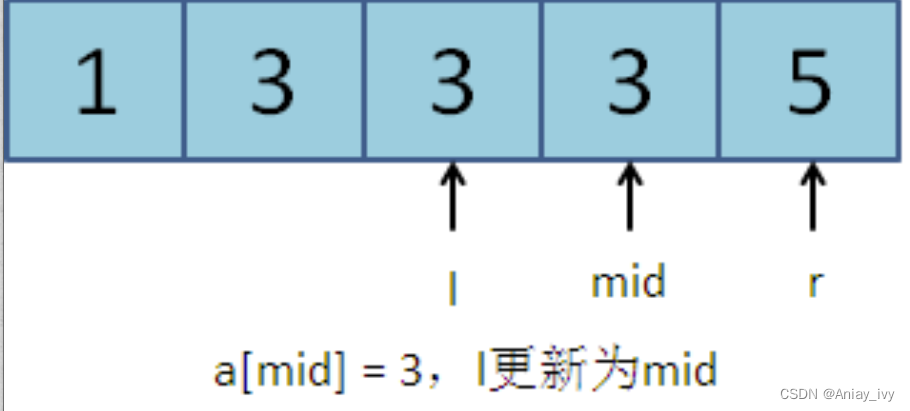
第二次：l = 2, r = 4, mid = (l + r) / 2 = 3。a[mid] = 3。符和更新规则2，l更新为mid：l = 3。

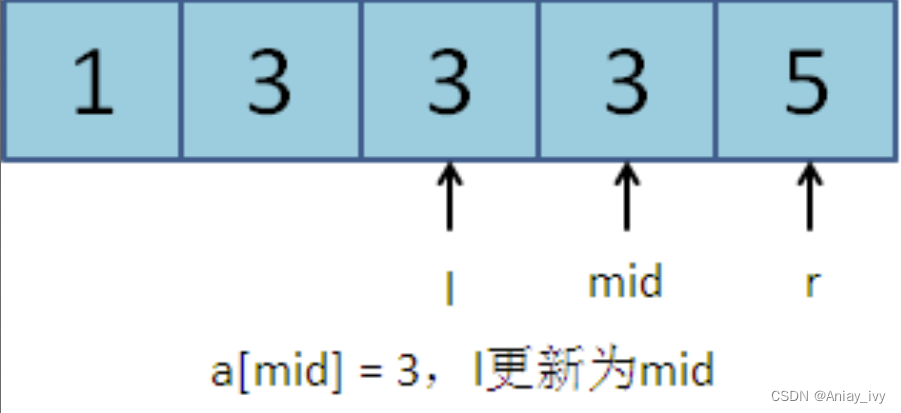
第三次：l = 3, r = 4, mid = (l + r) / 2 = 3。a[mid] = 3。符合更新规则2，l更新为mid：l = 3。

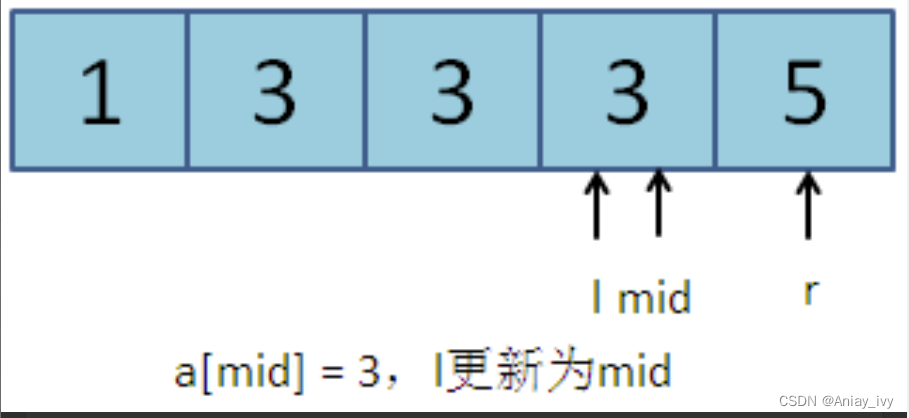
第四次：l = 3, r = 4, mid = (l + r) / 2 = 3。a[mid] = 3。符合更新规则2，l更新为mid：l = 3。

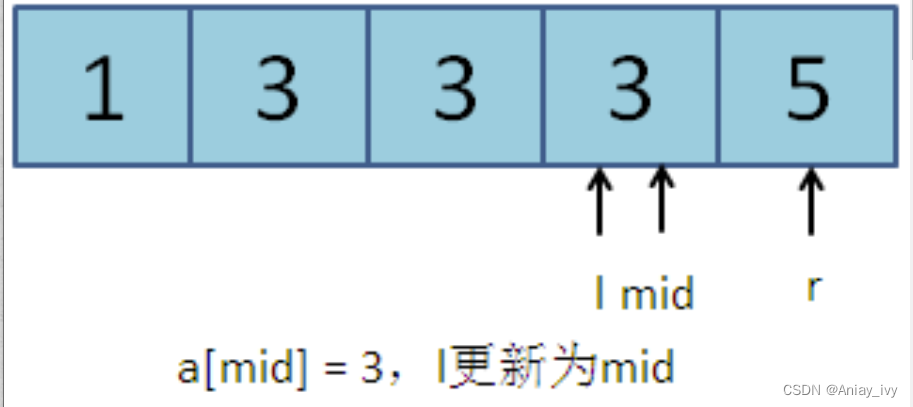
我们发现，从第三次开始陷入了死循环。

来看看为什么出现了这种情况

在第三次处理过程中，l = 3, r = 4。mid = (l + r) / 2 = 3。a[mid] = 3。l更新为mid：l = 3。
可以发现，l更新前的值为3，更新后，l的值为还为3。更新前后l的值没变，因此陷入了死循环。 原因在于：通过(l + r) / 2
计算mid的值，结果是向下取整的。在区间内只有两个元素的时，r的值可以用l + 1代替，因此mid = (l + r) / 2 = (l +
l + 1) / 2 = l。这个时候更新l = mid，l的值更新后依旧为l。 下次处理的区间和这次相同，陷入了死循环。
所以说：如果程序中出现了l = mid，因为整数除法结果是向下取整，所以l更新后的值可能等于更新前值，因此陷入死循环。

如何解决l = mid 陷入死循环的问题

想办法让l每次更新后的值都大于l，区间就能不断缩小，就不会陷入死循环。
具体的：让mid的取值为(l + r) /2向上取整，这样l更新为mid后，l更新后的值一定会大于更新前的值。

(l + r) / 2向上取整的值如何得到？

如果l + r为奇数，(l + r) / 2向上取整等于(l + r + 1) / 2向下取整；如果l + r为偶数，(l + r) /
2向上取整也等于(l + r + 1) / 2向下取整。因此，只要程序中有l = mid这种情况，mid就用mid = (l + r +1) / 2计算即可。
等等，这样会出引入一个新的问题

mid的值通过(l + r + 1) / 2 计算。在区间内只有两个元素的时，l的值可以用r - 1代替。因此mid = (l + r) /
2 = (r - 1 + r + 1) / 2 = r。如果程序用r = mid更新右边界，更新后r =r，区间不变，陷入死循环。所以，当程序中r的更新为r = mid 时，mid的值计算不能用 (l + r + 1) / 2。

总结：

1. mid 用(l + r) / 2计算时，如果程序中有l = mid ,程序会陷入死循环。
2. mid 用(l + r + 1) / 2计算时，如果程序中有r = mid ,程序会陷入死循环。

如何优雅的解决左右端点更新的问题？

1. 程序中不要同时出现l = mid, r = mdi这两条语句。

2. 如过程序中出现了l = mid，mid的值用 (l + r + 1) / 2计算。

3. 如果程序中出现了r = mid，mid的值用（(l + r) / 2计算。

2.2 何时停止二分

每次二分，通过更新l或r不断缩小区间，并保证答案一定在区间内。当区间内只有一个元素时，判断这个元素是否为答案，完成算法。

优雅的停止二分：

当l<r成立时，进行二分。l = r时停止。停止后进行判断，是答案输出，不是答案，此题无解。

 int l = 0, r = n;//n为初始时区间右端点，
    while(l < r){//l< r进行二分，l = r的时停止二分
        int mid = 中间点;
        if (更新r的条件成立)
            更新r;
        else
            更新l;
    }
    //循环结束时，[l,r]区间内只有一个元素
    if (区间内元素是答案)
        输出答案;
    else
        答案不存在;
我们写下上述例子的代码：

int findLast(vector<int> a,int t){
    int l = 0, r = a.size();
    while (l < r){//l<r进行二分，直到l=r时，停止二分
        int mid = (l + r + 1) / 2;//下方语句，出现了l = mid,mid要用(l + r + 1) / 2计算
        if (a[mid] > t)//a[mid] > t,t最后一次出现的位置一定在mdi之前
            r = mid - 1;
        else //a[mid] <= t,t最后一次出现的位置一定在mdi处或者mid之后
            l = mid;//出现了l = mid,mid要用(l + r + 1) / 2计算
    }
    //因为答案存在，并且二分过程中保证了答案一直在区间[l,r]中，当[l,r]中只有一个元素时，即为答案。
    return l;
}

如果题目改成求target第一次出现的位置，程序如下：

int findFirst(vector<int> a, int t){
    int l = 0, r = a.size();
    while (l < r){
        int mid = (l + r) / 2;//下方语句，出现了r = mid,mid要用(l + r ) / 2计算
        if (a[mid] >= t)//a[mid] >= t,t第一次出现的位置一定在mdi或者mid之前
            r = mid ;
        else //a[mid] < t,t第一次出现的位置一定在mid之后
            l = mid + 1;//出现了r = mid,mid要用(l + r) / 2计算
    }
    //因为答案存在，并且二分过程中保证了答案一直在区间[l,r]中，当[l,r]中只有一个元素时，即为答案。
    return l;
}

3. 二分法一定要有序才能使用吗？

3.1 先看一个例子
​ 设想另一个猜数字游戏：小明写下一个包含10个无序数字的序列，让小刚猜其中一个数字的位置。小刚每猜一次位置，小明会给提醒：目标在猜的位置左侧还是右侧。

依旧可以用二分法快速找到目标的位置。

例如：小明写下的序列为:[15,12,18,13,17,14,19,16,11,10]，要猜出19所在的位置。序列一共10个元素，分布在从0到9的位置。小刚可以这样猜：

第一次猜0–9的中间位置：(0 + 9) / 2 = 4。小明给出提醒：19在位置4的右侧。

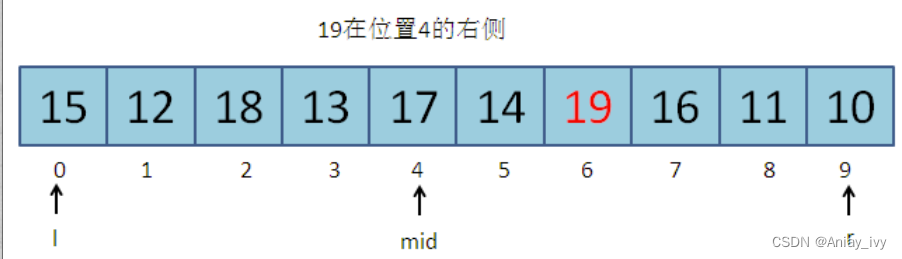
第二次猜5–9的中间位置：(5 + 9) / 2 = 7。小明给出提醒：19在位置7的左侧。

第三次猜5–7的中间位置：(5 + 7) / 2 = 6。19在位置6，游戏结束。

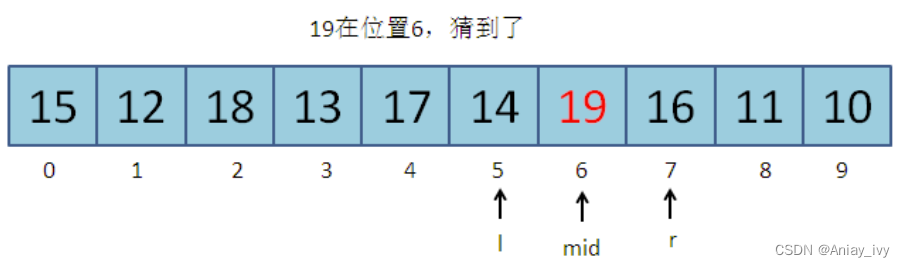
在猜数字过程中，只要能判断答案在猜的位置左边还是右边，就能更新区间。

3.2 使用二分法的关键
是否可以使用二分法的关键在于：二分后，能否判断出答案所在的区间，而不是数据是否有序。

同理，找数字最后一次出现位置的例子中，可以使用二分法是因为每次二分后，能通过中间值与目标值得大小关系判断出答案所在区间。关键点在于：二分后能判断出答案所在区间。如果数据无序，能通过其他方法确定答案所在区间，同样也可以使用二分法。

3.3 一道题目
给定一个包含整数的数组，每个元素都出现了两侧，并且相同元素相邻，唯有一个元素出现了一次，找出这个数字。

例如：数组a：为[3,3,8,8,9,1,1]。因为9只出现了一次，所以输出9。

数组是无序的，能不能使用二分法呢？关键在于二分后能判断出答案所在区间。

思考：

1. 数组中只有一个元素出现了一次，其他元素出现次2次。所以数组的元素个数一定为奇数个。

2. 如果中间的数字出现了两次，把这对数字去掉，数组会被分成左右两部分。出现了一次的数字，要么在左侧数组，要么在右侧数组。并且包含出现一次数字的数组，元素个数为奇数个；不包含出现一次数字的数组，元素个数为偶数个。
   

3. 如果中间数字出现了一次，这个数字就是答案。

思考2可以得出：二分后，答案在元素个数为奇数的那个数组中。所以可以使用二分法，代码如下。

class Solution {
public:
    int singleNonDuplicate(vector<int>& nums) {
        if(nums.size() == 1) return nums[0];//特殊情况先处理
        int l = 0, r = nums.size() - 1;
        while(l < r){
            int mid = l + (r - l >> 1);// >> 1,等价于除以2。
            if(nums[mid] == nums[mid + 1]){// a[mid]和后一个元素相等
                if((r - (mid + 1)) % 2 == 1) l = mid + 2;//右边有奇数个元素,答案在右边，更新l
                else r = mid - 1;//左边有奇数个元素,答案在左边，更新r
            }
            else if(nums[mid] == nums[mid -1]){// a[mid]和前一个元素相等
                if((r - mid) % 2 == 1) l = mid + 1;//右边有奇数个元素,答案在右边，更新l
                else r = mid - 2;//左边有奇数个元素,答案在左边，更新r
            }
            else
                return nums[mid];//a[mid]与前一个后一个元素都不等,该元素就是答案
        }
        return nums[l];//只剩一个元素，就是答案。
    }
};

4. 如何优雅的证明二分法的时间复杂度是O(logn)？

二分法每次区间长度缩小为原来的二分之一。当区间内只有一个元素时停止。

设开始时数组中元素个数为n。

第一次二分后：答案所在区间长度缩小一半：n / 2。

第二次二分后：答案所在区间长度缩小一半：n / 4。

…

第k次二分后：答案所在区间长度缩小一半：n / 2^k。

…

第logn次二分后：答案所在区间长度缩小一半：n / 2^logn = 1，停止二分。

总共处理了logn次，每次处理的时间复杂度是O(1)。所以总时间复杂是O(logn)。

例题

给定一个浮点数 n，求它的三次方根。

输入格式

共一行，包含一个浮点数 n。

输出格式 共一行，包含一个浮点数，表示问题的解。

注意，结果保留 6位小数。

数据范围 −10000≤n≤10000

输入样例：

1000.00

输出样例：

10.000000

代码

#include <iostream>
using namespace std;
double n;
int main(){
    cin >> n;
    // 答案区间
    double l = -100, r = 100;
    // 二分答案区间
    for(int i = 0; i < 10000; i++){
        // 取中点
        double mid = (l + r) / 2;
        // 收缩区间
        if(mid * mid * mid < n) l = mid;
        else r = mid;
    }
    // 输出结果
    printf("%.6f", l);
}

这里面的a，b要根据具体二分的范围来指定，对于c的值，如果题目中要求保留4位小数，c取1e-6,如果题目中要求保留6位小数，那c取1e-8

java:

import java.io.*;

class Main{

    public static void main(String[]args)throws IOException{
        BufferedReader in=new BufferedReader(new InputStreamReader(System.in));
        double n=Double.parseDouble(in.readLine());

        double l=-1000;
        double r=1000;
        while(r-l>1e-8){
            double mid=(l+r)/2;
            if(mid*mid*mid<n) l=mid;
            else r=mid;
        }

        System.out.printf("%.6f\n",l);
    }
}