[从0开始AIGC]: 如何区分并记住常见的几种 Normalization 算法

如何区分并记住常见的几种 Normalization 算法

文章目录

如何区分并记住常见的几种 Normalization 算法

1.为什么要用归一化操作

1.1 内部协变量偏移（Internal Covariate Shift）

在介绍归一化操作之前，我们需要了解什么是内部协变量偏移。首先，协变量偏移是数据分布不一致的一种表现。已知贝叶斯公式：
$p(\mathbf{x},y)=p(\mathbf{x}|y)p(y)=p(y|\mathbf{x})p(\mathbf{x})$
所谓协变量偏移指的是：源域和目标域的输入边际分布不同 $p_S(\mathbf{x})≠p_T(\mathbf{x})$ ，但两者的后验分布相同 $p_S(y|\mathbf{x})=p_T(y|\mathbf{x})$ ，即学习任务相同。

而在深度神经网络中，中间某一层的输入是其之前的神经层的输出。因此，其之前的神经层的参数变化会导致其输入的分布发生较大的差异。在使用随机梯度下降来训练网络时，每次参数更新都会导致网络中间每一层的输入的分布发生改变。 越深的层，其输入的分布会改变得越明显。就像一栋高楼，低楼层发生一个较小的偏移，都会导致高楼层较大的偏移。

从机器学习的角度来看，如果某一层网络的输入的分布发生了变化，那么其参数就需要重新学习，我们将这种现象称为内部协变量偏移。归一化方法的引入可以使得每一个神经层的输入的分布在训练过程中保持一致。

1.2 梯度弥散

梯度弥散指的是，梯度在反向传播过程中由于网络太深或者网络激活值位于激活函数的饱和区而消失，深层的梯度无法顺利传播到神经网络的浅层，进而导致神经网络无法正常训练。

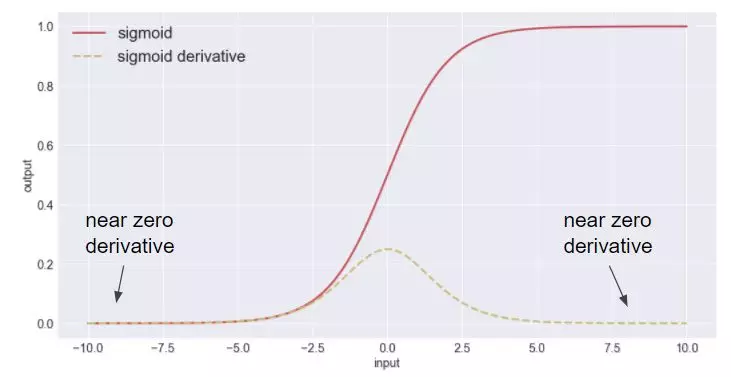
如上图常用的sigmoid激活函数，虚线为导数。当函数输入位于饱和区（函数值趋近于0或者1）时，梯度将接近为0。

那么如何解决这一现象呢？

一种做法是在网络的结构上做文章，例如ResNet中引入了跨层连接，梯度可以通过跨层连接传入底层网络层；
另一种做法就是将激活函数的输入限制在非饱和区。

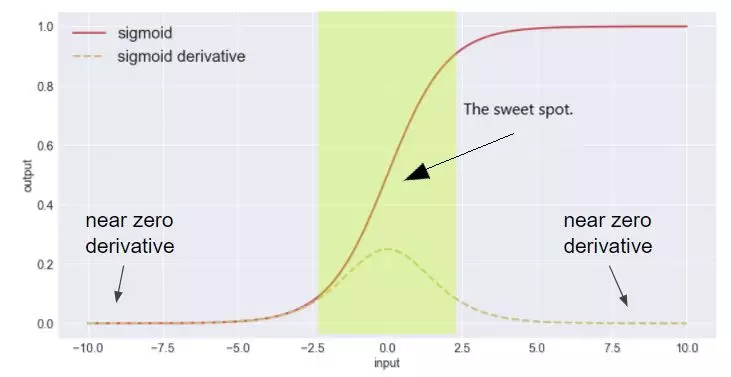
通过使用归一化操作便可以达到这一目的。对网络层的输入进行归一化后，输入的数值便被限制在较小的区间进而保证了输入不会进入激活函数的饱和区。但是，直接将网络层的净输入归一化到[−1,1]区间会使得激活函数的取值区间限制在线性变换区间内，减弱了神经网络的非线性性质。因此，为了使得归一化不对网络的表示能力造成负面影响，可以通过一个附加的缩放和平移变换改变取值区间。

2. 神经网络中常见的归一化方法

神经网络中有各种归一化算法：Batch Normalization (BN)、Layer Normalization (LN)、Instance Normalization (IN)、Group Normalization (GN)。从公式看它们都差不多，如下述公式所示：无非是计算出均值方差，然后减去均值，除以标准差，再施以线性映射。
$y=\gamma(\frac{x-\mu(x)}{\sigma(x)})+\beta$
上述这些归一化算法的主要区别在于操作的 feature map 维度不同。如何区分并记住它们，一直是件令人头疼的事。本文目的不是介绍各种归一化方式在理论层面的原理或应用场景，而是结合 pytorch 代码，介绍它们的具体操作，并给出一个方便记忆的类比。

2.1 Batch Normalization

Batch Normalization (BN) 是最早出现的，对于卷积神经网络通常也是效果最好的归一化方式。feature map的维度为：
$x\in \mathbb{R}^{N\times C\times H \times W}$
包含N个样本，每个样本通道数为C，高为H，宽为W。对其求均值和方差时，将在 N、H、W上操作，而保留通道 C 的维度。具体来说，就是把第1个样本的第1个通道，加上第2个样本第1个通道 … 加上第 N 个样本第1个通道，求平均，得到通道 1 的均值（注意是除以 N×H×W 而不是单纯除以 N，最后得到的是一个代表这个 batch 第1个通道平均值的数字，而不是一个 H×W 的矩阵）。求通道 1 的方差也是同理。对所有通道都施加一遍这个操作，就得到了所有通道的均值和方差。对于任意一个通道 $c\in C$ ，均值方差的具体计算公式为：

$\mu_c(x)=\frac{1}{NHW}\sum_{n=1}^{N}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw}$

$\sigma(x)=\sqrt{\frac{1}{NHW}\sum_{n=1}^{N}\sum_{h=1}^{H}\sum_{w=1}^{W}(x_{nchw}-\mu_c(x))^2+\epsilon}$

如果把
$x\in \mathbb{R}^{N\times C\times H \times W}$
类比为一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 W 个字符。BN 求均值时，相当于把N本书按相同的页码一一对应地加起来（例如第1本书第36页，第2本书第36页…），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求“平均书”的操作（注意这个“平均书”有C页，每页只有一个字），求标准差时也是同理。

我们可以在 pytorch 下自己写一个 BN ，看看和官方的版本是否一致，以检验上述理解是否正确：

# coding=utf8
import torch
from torch import nn

# track_running_stats=False，求当前 batch 真实平均值和标准差，
# 而不是更新全局平均值和标准差
# affine=False, 只做归一化，不乘以 gamma 加 beta（通过训练才能确定）
# num_features 为 feature map 的 channel 数目
# eps 设为 0，让官方代码和我们自己的代码结果尽量接近
bn = nn.BatchNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)

# 乘 10000 为了扩大数值，如果出现不一致，差别更明显
x = torch.rand(10, 3, 5, 5)*10000 
official_bn = bn(x)

# 把 channel 维度单独提出来，而把其它需要求均值和标准差的维度融合到一起
x1 = x.permute(1,0,2,3).view(3, -1)
 
mu = x1.mean(dim=1).view(1,3,1,1)
# unbiased=False, 求方差时不做无偏估计（除以 N-1 而不是 N），和原始论文一致，
# 个人感觉无偏估计仅仅是数学上好看，实际应用中差别不大
std = x1.std(dim=1, unbiased=False).view(1,3,1,1)

my_bn = (x-mu)/std

diff=(official_bn-my_bn).sum()
print('diff={}'.format(diff)) # 差别是 10-5 级的，证明和官方版本基本一致；采用无偏估计，差别在10-6级

2.2 Layer Normalization

BN 的一个缺点是需要较大的 batchsize 才能合理估训练数据的均值和方差，这导致内存很可能不够用，同时它也很难应用在训练数据长度（时间维度或者Channel维度）不同的 RNN 模型上。Layer Normalization (LN) 的一个优势是不需要批训练，在单条数据内部就能归一化。

对于
$x\in \mathbb{R}^{N\times C\times H \times W}$
，LN 对每个样本的 C、H、W 维度上的数据求均值和标准差，保留 N 维度。对于batch中第n个样本，其均值和标准差公式为：
$\mu_n(x)=\frac{1}{CHW}\sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw}$

$\sigma_n(x)=\sqrt{\frac{1}{CHW}\sum_{c=1}^{C}\sum_{h=1}^{H}\sum_{w=1}^{W}(x_{nchw}-\mu_n(x))^2+\epsilon}$
把一个 batch 的 feature 类比为一摞书 N。LN 求均值时，相当于把某一本书 n 的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”，求标准差时也是同理。

如下代码对比了 pytorch 官方 API 计算 LN，和依据原理逐步计算 LN 得到的结果：

import torch
from torch import nn

x = torch.rand(10, 3, 5, 5)*10000

# normalization_shape 相当于告诉程序这本书有多少页，每页多少行多少列
# eps=0 排除干扰
# elementwise_affine=False 不作映射
# 这里的映射和 BN 以及下文的 IN 有区别，它是 elementwise 的 affine，
# 即 gamma 和 beta 不是 channel 维的向量，而是维度等于 normalized_shape 的矩阵
ln = nn.LayerNorm(normalized_shape=[3, 5, 5], eps=0, elementwise_affine=False)

official_ln = ln(x)

x1 = x.view(10, -1)
mu = x1.mean(dim=1).view(10, 1, 1, 1)
std = x1.std(dim=1,unbiased=False).view(10, 1, 1, 1)

my_ln = (x-mu)/std

diff = (my_ln-official_ln).sum()

print('diff={}'.format(diff)) # 差别和官方版本数量级在 1e-5

CNN中的LN和Transformer中的LN：
# features: (bsz, max_len, hidden_dim)
# 
class LayerNorm(nn.Module):
def __init__(self, features, eps=1e-6):
	super(LayerNorm, self).__init__()
	self.a_2 = nn.Parameter(torch.ones(features))
	self.b_2 = nn.Parameter(torch.zeros(features))
	self.eps = eps

def forward(self, x):
	# 就是在统计每个样本每个时间步所有维度的值，求均值和方差，所以就是在hidden dim上操作
	# 相当于变成[bsz*max_len, hidden_dim], 然后再转回来, 保持是三维
	mean = x.mean(-1, keepdim=True) # mean: [bsz, max_len, 1]
	std = x.std(-1, keepdim=True) # std: [bsz, max_len, 1]
    # 注意这里也在最后一个维度发生了广播
	return self.a_2 * (x - mean) / (std + self.eps) + self.b_2
BN还是LN？

LN特别适合处理变长数据，因为是对channel维度做操作(这里指NLP中的hidden维度)，和句子长度和batch大小无关

对于NLP data来说，batch上去做归一化是没啥意义的，因为不同句子的同一位置的分布大概率是不同的。

BN就是在每个维度上统计所有样本的值，计算均值和方差；LN就是在每个样本上统计所有维度的值，计算均值和方差（注意，这里都是指的简单的MLP情况，输入特征是（bsz，hidden_dim））。所以BN在每个维度上分布是稳定的，LN是每个样本的分布是稳定的。

LN变体

1. RMSNorm

RMS Norm全称是Root Mean Square Layer Normalization，与RMS Norm是基于LN的一种变体，主要是去掉了减去均值的部分(去Center)，计算公式如下：
$\overline{a}_i=\frac{a_i}{ \mathbf {RMS(a)}}g_i, \ \ \ \mathbf{where\ RMS(a)}=\sqrt{\frac{1}{n}\sum_{i=1}^{n}a_i^2}$
这里的 $a_i$ 与LN中的x等价，相比于LN，可以发现，不论是分母的方差和分子不分，都取消了均值计算，经作者在各种场景中实验发现，减少约 7%∼64% 的计算时间。

一个直观的猜测是，center操作，类似于全连接层的bias项，储存到的是关于预训练任务的一种先验分布信息，而把这种先验分布信息直接储存在模型中，反而可能会导致模型的迁移能力下降。所以T5不仅去掉了Layer Normalization的center操作，它把每一层的bias项也都去掉了。

这篇论文中，作者又提出了partial RMSNorm，简称pRMSNorm，就是只对一个token的尾部求取其方差，在真正计算的时候，token的embedding每个value，只会使用部分计算出来的方差。

class RMSNorm(nn.Module):
    def __init__(self, dim):
        super().__init__()
        self.scale = dim ** 0.5
        self.g = nn.Parameter(torch.ones(dim))

    def forward(self, x):
        return F.normalize(x, dim = -1) * self.scale * self.g

F.normalize函数：

参数：

input（张量）：要归一化的输入张量。

p（浮点数，可选）：计算范数时的幂值。默认值为 2。

dim（整数，可选）：要减小的维度。默认值为 1。

eps（浮点数，可选）：防止除以零的小值。默认值为 1e-12。

数学公式是：

$normalized\_tensor[i]=\frac{input\_tensor[i]}{\sqrt{\sum_{j=1}^{n}(input\_tensor[j])^p}+\epsilon}$

其中：

input_tensor[i] 是输入张量的第 i 个元素，

n 是输入张量的元素数量，

p 是范数的阶数（默认为 2，即 L2 范数），

$\epsilon$ 是一个很小的数，用于防止除以零（默认为 1e-12）。

这个公式将每个元素除以输入张量的 p 阶范数，得到的结果就是归一化后的张量。这样做可以确保归一化后的张量的元素值在 -1 和 1 之间，且其 p 阶范数为 1。

2. DeepNorm

Deep Norm是对LN的的改进，主要有两点改进，其中 $\alpha$ 和 $\beta$ 都是根据模型的Encoder（N）和Decoder（M）层数计算出来的，通过如下方案，作者把模型的层数提升到了1000+。

DeepNorm在进行Layer Norm之前，会以 $\alpha$ 参数扩大input输入
在Xavier参数初始化过程中以 $\beta$ 减小部分参数的初始化范围

具体方案如下：

2.3 Instance Normalization

Instance Normalization (IN) 最初用于图像的风格迁移。作者发现，在生成模型中， feature map 的各个 channel 的均值和方差会影响到最终生成图像的风格，因此可以先把图像在 channel 层面归一化，然后再用目标风格图片对应 channel 的均值和标准差“去归一化”，以期获得目标图片的风格。IN 操作也在单个样本内部进行，不依赖 batch。

对于
$x\in \mathbb{R}^{N\times C\times H \times W}$
，IN 对每个样本的 H、W 维度的数据求均值和标准差，保留 N 、C 维度，也就是说，它只在 channel 内部求均值和标准差，其公式为：
$\mu_{nc}(x)=\frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw}$

$\sigma_{nc}(x)=\sqrt{\frac{1}{HW}\sum_{h=1}^{H}\sum_{w=1}^{W}(x_{nchw}-\mu_{nc}(x))^2+\epsilon}$
IN 求均值时，相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每本书每页的“平均字”，求标准差时也是同理。

如下代码对比了 pytorch 官方 API 计算 IN，和依据原理逐步计算 IN 得到的结果：

import torch
from torch import nn


x = torch.rand(10, 3, 5, 5) * 10000

# track_running_stats=False，求当前 batch 真实平均值和标准差，
# 而不是更新全局平均值和标准差
# affine=False, 只做归一化，不乘以 gamma 加 beta（通过训练才能确定）
# num_features 为 feature map 的 channel 数目
# eps 设为 0，让官方代码和我们自己的代码结果尽量接近
In = nn.InstanceNorm2d(num_features=3, eps=0, affine=False, track_running_stats=False)

official_in = In(x)

x1 = x.view(30, -1)
mu = x1.mean(dim=1).view(10, 3, 1, 1)
std = x1.std(dim=1, unbiased=False).view(10, 3, 1, 1)

my_in = (x-mu)/std

diff = (my_in-official_in).sum()
print('diff={}'.format(diff)) # 误差量级在 1e-5

2.4 Group Normalization

Group Normalization (GN) 适用于占用显存比较大的任务，例如图像分割。对这类任务，可能 batchsize 只能是个位数，再大显存就不够用了。而当 batchsize 是个位数时，BN 的表现很差，因为没办法通过几个样本的数据量，来近似总体的均值和标准差。GN 也是独立于 batch 的，它是 LN 和 IN 的折中。正如提出该算法的论文展示的：

GN 计算均值和标准差时，把每一个样本 feature map 的 channel 分成 G 组，每组将有 C/G 个 channel，然后将这些 channel 中的元素求均值和标准差。各组 channel 用其对应的归一化参数独立地归一化。
$\mu_{ng}(x)=\frac{1}{(C/G)HW}\sum_{c=gC/G}^{(g+1)C/G}\sum_{h=1}^{H}\sum_{w=1}^{W}x_{nchw}$

$\sigma_{ng}(x)=\sqrt{\frac{1}{(C/G)HW}\sum_{c=gC/G}^{(g+1)C/G}\sum_{h=1}^{H}\sum_{w=1}^{W}(x_{nchw}-\mu_{ng}(x))^2+\epsilon}$
继续用书类比。GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，求每个小册子的“平均字”和字的“标准差”。

如下代码对比了 pytorch 官方 API 计算 GN，和依据原理逐步计算 GN 得到的结果：

import torch
from torch import nn


x = torch.rand(10, 20, 5, 5)*10000

# 分成 4 个 group
# 其余设定和之前相同
gn = nn.GroupNorm(num_groups=4, num_channels=20, eps=0, affine=False)
official_gn = gn(x)

# 把同一 group 的元素融合到一起
x1 = x.view(10, 4, -1)
mu = x1.mean(dim=-1).reshape(10, 4, -1)
std = x1.std(dim=-1).reshape(10, 4, -1)

x1_norm = (x1-mu)/std
my_gn = x1_norm.reshape(10, 20, 5, 5)

diff = (my_gn-official_gn).sum()

print('diff={}'.format(diff)) # 误差在 1e-4级

3. Post-LN&Pre-LN

Pre Norm和Post Norm的式子分别如下：
$Pre Norm: x_{t+1}=x_t+F_t(Norm(x_t))\\Post Norm: x_{t+1}=Norm(x_t+F_t(x_t))$
图形化的方式可能更加直观，前一个是Post，后一个是Pre。

https://openreview.net/pdf?id=B1x8anVFPr

为什么Pre效果弱于Post

Pre Norm中多层叠加的结果更多是增加宽度而不是深度，层数越多，这个层就越“虚”。Pre Norm结构无形地增加了模型的宽度而降低了模型的深度，而我们知道深度通常比宽度更重要，所以是无形之中的降低深度导致最终效果变差了。而Post Norm刚刚相反，它每Norm一次就削弱一次恒等分支的权重，所以Post Norm反而是更突出残差分支的， 因此Post Norm中的层数更加有分量，起到了作用，一旦训练好之后效果更优。

以上解释来源于苏神的博客，更详细的内容可以参考：为什么Pre Norm的效果不如Post Norm？

4. 总结

这里再重复一下上文的类比。如果把
$x\in \mathbb{R}^{N\times C\times H \times W}$
类比为一摞书，这摞书总共有 N 本，每本有 C 页，每页有 H 行，每行 W 个字符。

计算均值时

BN 相当于把这些书按页码一一对应地加起来（例如：第1本书第36页，加第2本书第36页…），再除以每个页码下的字符总数：N×H×W，因此可以把 BN 看成求“平均书”的操作（注意这个“平均书”每页只有一个字）
LN 相当于把每一本书的所有字加起来，再除以这本书的字符总数：C×H×W，即求整本书的“平均字”
IN 相当于把一页书中所有字加起来，再除以该页的总字数：H×W，即求每页书的“平均字”
GN 相当于把一本 C 页的书平均分成 G 份，每份成为有 C/G 页的小册子，对这个 C/G 页的小册子，求每个小册子的“平均字”