文章目录
739. 每日温度
题目链接
标签
栈 数组 单调栈
思路
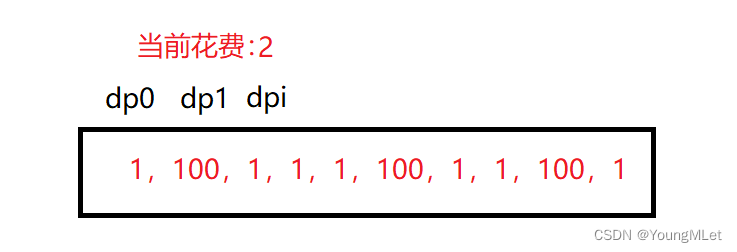
本题求解的是:对于第 i 天,下一个更高温度出现在几天后。抽象一下,就是 求 每个元素之后的更大元素的索引 与 当前元素索引 之差。
可以使用 单调栈 的思想解决,维护一个 从栈顶到栈底 温度 单调递增 的栈,这个栈存储未找到等待天数的天的索引。
遍历温度数组,对于第 i 天的温度 temp,如果 栈中有索引 prevIndex(这个索引取自 栈顶,是整个栈中温度最小的天的索引) 并且 该索引指向的温度比 temp 小,则 第 prevIndex 天的下一个更高温度出现在 i - prevIndex 天之后,它找到了自己的等待天数,可以将其移出栈中。重复这步操作,直到 没有未找到等待天数的天(栈中有索引) 或 第 prevIndex 天的温度比 temp 高。
可以发现:在栈中,越靠近栈顶,索引指向的温度越低;越靠近栈底,索引指向的温度越高。这就是 单调栈,它能解决 求每个元素之后的更大元素 的问题,稍微变形就变成了本题。
代码
class Solution {
public int[] dailyTemperatures(int[] temperatures) {
int len = temperatures.length;
int[] res = new int[len];
LinkedList<Integer> stack = new LinkedList<>(); // 存储 未找到等待天数 的天的索引
for (int i = 0; i < len; i++) {
int temp = temperatures[i]; // 获取第 i 天的温度
// 给 未找到等待天数 的每天 赋 等待天数 的值
// 直到 没有未找到等待天数的天的索引 或 之前有一天温度更高
while (!stack.isEmpty() && temp > temperatures[stack.peek()]) {
int prevIndex = stack.pop(); // 取出 未找到等待天数 的天数
res[prevIndex] = i - prevIndex; // 保存等待天数
}
stack.push(i); // 将 i 放到栈中,为它寻找更高温度
}
return res;
}
}
82. 删除排序链表中的重复元素 II
题目链接
标签
链表 双指针
思路
本题是去除链表中重复的所有元素,本质上是 删除节点,删除一个节点就是 让前一个节点指向后一个节点,跳过这个节点。发现这里使用到了 前一个节点,所以使用 哨兵节点 指向链表,避免 对删除第一个节点 进行的特殊处理。
要删除多个重复节点,除了原有的 前一个节点的指针 prev 和 这个节点的指针 curr 之外,还得使用一个指针 after,after 指向不与 curr 重复的节点,最后得让 prev 指向 after,从而删除 从 prev 到 after 之间的多个重复节点。
如果没有遇到重复节点,就让 prev 正常向右移动,并更新 curr, after。
代码
class Solution {
public ListNode deleteDuplicates(ListNode head) {
ListNode sentinel = new ListNode(0, head); // 哨兵节点,指向原始链表
ListNode prev = sentinel; // 指向待检查节点,是它的前一个节点
ListNode curr; // curr 是待检查节点
ListNode after; // after 是待检查节点的下一个节点,它最终指向不与 curr 重复的节点
// 给 curr, after 赋值,并在它两个中有一个为 null 时退出循环
while ((curr = prev.next) != null && (after = curr.next) != null) {
if (curr.val != after.val) { // 如果 after 不与 after 重复
prev = prev.next; // 则让 prev 正常向右移动
continue;
}
// 找到不与 curr 重复的节点,null 也算不与 curr 重复
while ((after = after.next) != null && after.val == curr.val) {
continue;
}
prev.next = after; // 让 prev 指向这个节点
}
return sentinel.next; // 返回哨兵节点指向的链表
}
}
106. 从中序与后序遍历序列构造二叉树
题目链接
标签
树 数组 哈希表 分治 二叉树
思路
本题和 105. 从前序与中序遍历序列构造二叉树 十分相似,不过本题考查的是 中序遍历 和 后序遍历。
二叉树的三种遍历
先讲一讲二叉树的三种 (深度优先搜索) 遍历:
- 前序遍历:先处理本节点的值,再遍历左子树,最后遍历右子树。
- 中序遍历:先遍历左子树,再处理本节点的值,最后遍历右子树。
- 后序遍历:先遍历左子树,再遍历右子树,最后处理本节点的值。
例如对于下图:

它的三种遍历结果分别如下:
- 前序遍历:
[4, 2, 1, 3, 6, 5, 7]。
可以这样分:[4], [2, 1, 3], [6, 5, 7],分别为:本节点、左子树、右子树。
左子树有三个节点的原因是:中序遍历的本节点[4]前有 3 个元素。 - 中序遍历:
[1, 2, 3, 4, 5, 6, 7]。
可以这样分:[1, 2, 3], [4], [5, 6, 7],分别为:左子树、本节点、右子树。
本节点为[4]的原因是:前序遍历的第一个元素是4或 后序遍历的最后一个元素是4。 - 后序遍历:
[1, 3, 2, 5, 7, 6, 4]。
可以这样分:[1, 3, 2], [5, 7, 6], [4],分别为:左子树、右子树、本节点。
左子树有三个节点的原因是:中序遍历的本节点[4]前有 3 个元素。
由此可见:只要有中序遍历,再加上前序遍历或后序遍历的其中一种,就可以构建一颗二叉树。
值与索引的映射
在构建二叉树时,获取后序遍历的某一个值作为根节点,然后要根据这个值将中序遍历的结果划分成两部分,为了方便划分,可以使用一个 Map 来存储中序遍历的 值 与 索引 的映射。
对于后序遍历的使用
仔细观察后序遍历的结果 [1, 3, 2, 5, 7, 6, 4],可以发现一个很奇妙的东西:从后到前,4 是根节点,6 是右子树的根节点,7, 5 是右子树的两个子节点(也算是两个 null 的根节点),2 是左子树的根节点,3, 1 是左子树的两个子节点(也算是两个 null 的根节点)。
在使用递归的前提下,如果 先构建右子树,再构建左子树,最后返回本次构建的树,就可以把 倒序遍历 postorder 的结果 作为每棵树(或子树)的根节点。
对于中序遍历的使用
在区间 [inLeft, inRight] 上构建二叉树时,先通过后序遍历找根节点的值 rootVal,然后通过 Map 寻找这个值在中序遍历中对应的索引 index,接着进行划分:在区间 [index + 1, inRight] 上构建右子树,在区间 [inLeft, index - 1] 上构建左子树。最后将本次在区间 [inLeft, inRight] 上构建的二叉树返回。
代码
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
// 初始化成员变量
this.inorder = inorder;
this.postorder = postorder;
this.postIndex = postorder.length - 1;
for (int i = 0; i < inorder.length; i++) { // 构建中序遍历的 值 与 索引 的映射
this.indcies.put(inorder[i], i);
}
return build(0, inorder.length - 1);
}
private int postIndex; // postorder 数组的索引,指向正在构建的树的根节点
private int[] inorder; // 中序遍历数组
private int[] postorder; // 后序遍历数组
// 中序遍历的 值 与 索引 的映射,key 为 值,value 为 值在中序遍历数组中的索引
private Map<Integer, Integer> indcies = new HashMap<>();
// 在中序遍历数组的 [inLeft, inRight] 区间内,构建树
private TreeNode build(int inLeft, int inRight) {
if (inLeft > inRight) { // 如果区间内没有节点
return null; // 则不需要建立二叉树,退出递归
}
int rootVal = postorder[postIndex]; // postIndex 指向 postorder 中当前树的根节点的值
int index = indcies.get(rootVal); // 获取当前根节点的值在 中序遍历数组 中的索引
TreeNode root = new TreeNode(rootVal); // 新建当前树的根节点
// 先构建右子树,再构建左子树,最后返回本次构建的二叉树
postIndex--; // 让 postIndex 指向右子树的根节点
root.right = build(index + 1, inRight); // 构建完右子树后,postIndex 指向左子树的根节点
root.left = build(inLeft, index - 1);
return root;
}
}