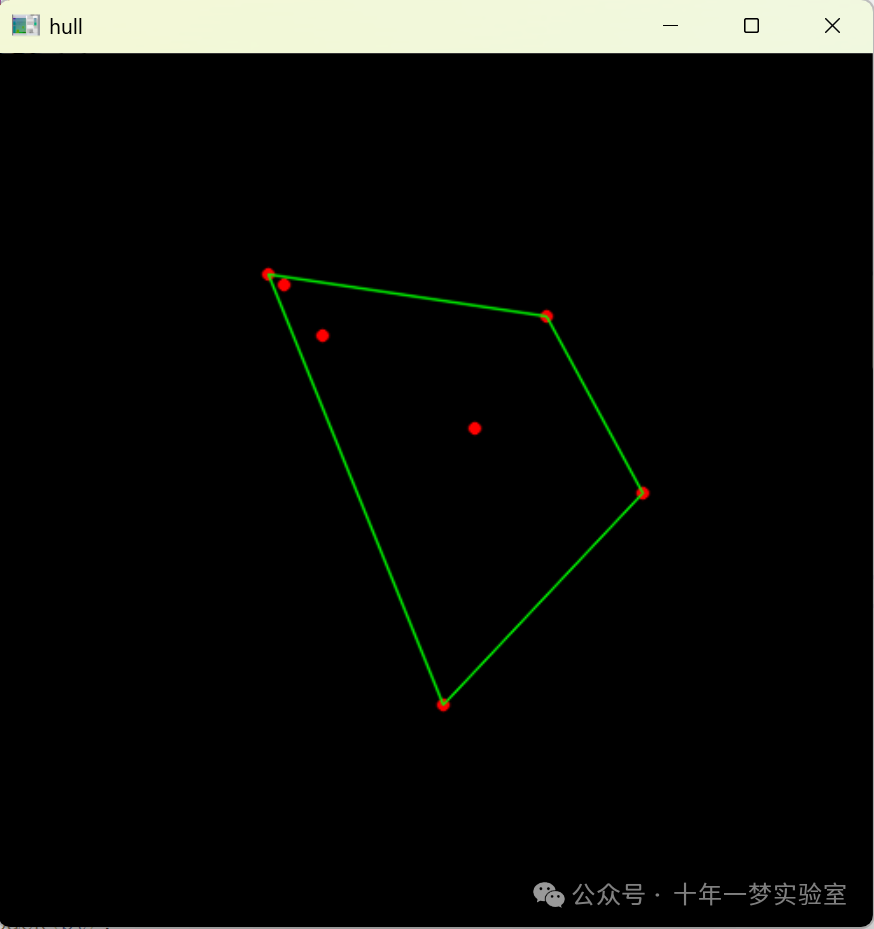
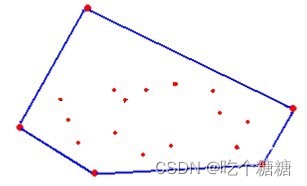
增量构造
在前面两篇博客:
清华计算几何-ConvexHull(凸包)-求极点InTriangle/ToLeft Test
分别介绍了EP(extremity point)和ED(extremity edge)求凸包的算法, 算法复杂度分别为O(n4)和O(n3). 这两种算法都是从一个集合里现存数据直接暴力求解出凸包.
增量构造的思路可以帮助我们进一步优化算法复杂度, 基本思路是:
一个个元素添加, 看每步的增量是否满足凸包要求.和插入排序的理念相似.


In-Convex-Polygon Test

(上图里的流程只包含了求解新的点是否是极点,并没包含判断旧点从极点变为非极点的剔除过程)
在每次插入新点的时候, 需要判断新点是极点还是非极点,采用二分法查找最终化解为in-triangle-test问题.找到相应位置, 如果为极点,则插入。思路基本和二分查找插入排序一样。
查找算法复杂度O(logn), 而进行了N点加点。二分查找在这里意义不大,下面分析原因.
二分法的无效性
本质上来说二分查找法在这里是无意义的或者说意义不大, 因为二分查找插入排序和普通插入排序的算法度都是O(n2). 二分查找插入排序只是加快查找的效率, 比普通插入排序快, 但快得不多. 因为"二分"这个概念意味着必须使用类似数组的数据结构, 进行insert插入。而数组insert插入算法复杂度是O(n).
极点模式判断法
判断新点为极点,并移除非极点
假设加入一个新点X, 如果新点X为新的极点,则满足如下图形

逆时针来看, 将X和任意一个极点V相连, V存在前点A和后点B, 如果

对每个凸包的每个极点V做如下运算

如果X为新的极点,得到的V结果模式存在四种:

t: 两次toleft测试都为R,经过的xt线可称为切线
s: 两次toleft测试都为L,经过的xs线可称为切线
st: 两次toleft测试结果分别R和L,这部分的点后续被保留。
ts: 两次toleft测试结果分别L和R,这部分的点后续被剔除。
也就是新点X成为极点,并插入到点t和点s之间。
判断新点为非极点
如果一个新点X不为极点,在凸包的内部, 则为如下图形

用上面的逆时针二次left-test判断法,对于任意一点V,前后点to-left-test测试结果只是RL。
极点模式判断法的算法复杂度为O(n2)
参考资料
[1]清华计算几何 P17-P2