《机器学习》读书笔记：总结“第4章 决策树”中的概念

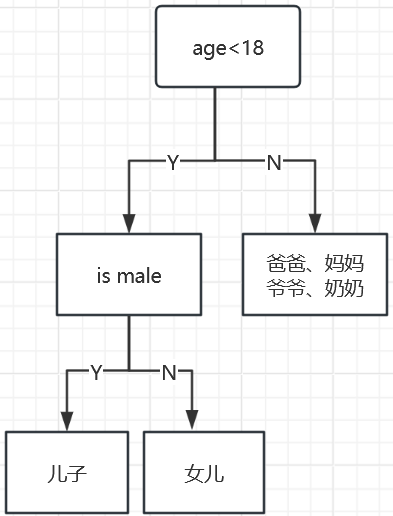
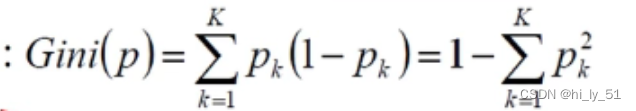💠决策树

基于树结构进行决策。

一棵决策树包括：

• 一个 根节点（起点）
• 若干 叶节点（没有下游节点的节点）
• 若干 内部节点(分支节点)

即：

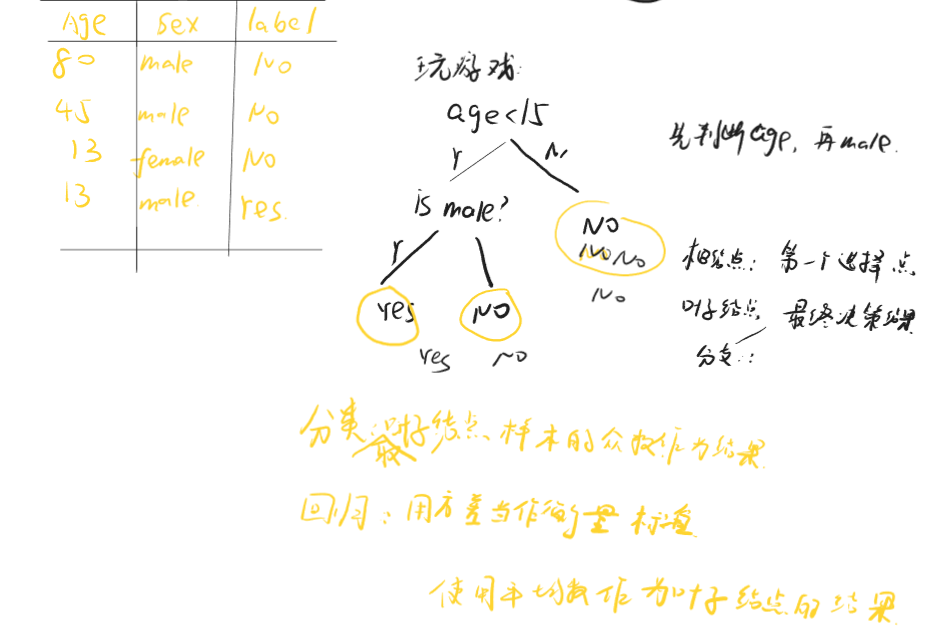
💠决策树学习基本算法：分而治之（divide and conquer）

训练集：$D=\{({\mathbf{x}}_1,y_1),({\mathbf{x}}_2,y_2),...，({\mathbf{x}}_m,y_m)\}$
其中的 $y$ 是标记，即分类，其值可能是$C_1$、$C_2$、…$C_n$。
其中 $\mathbf{x}$ 的属性集 A = { a 1 , a 2 , . . . , a d } A=\{a_1,a_2,...,a_d\} A={a1​,a2​,...,ad​}

这个算法是一个递归函数：
（笔者标记：这里的伪代码和原文不一样。一是我改变了一些表述与排版使我自己更容易理解；二是原文第12行的 “return” 我认为不对，又或者那里的 “return” 并非C++中的 “从函数返回”，而是 “从循环中返回”。不管怎样，我改成了符合C++语法习惯的伪代码）

TreeGenerate($D$, $A$)
{
····创建一个节点 node

····if ($D$中的样本全属于同一类别$C$)
····{
········node = “输出是$C$的叶节点”
········return node
····}

····if ($A$ 为空) or ($D$在$A$上取值相同)
····{
········令$C$是$D$中样本最多的分类
········node = “输出是$C$的叶节点”
········return node
····}

····从$A$中选择最优划分属性$a_{\ast }$ （关键步骤）
····for ($a_{\ast }$中的每一个值$a_{\ast }^v$)
····{
········在 node 下创建一个分支节点 node_child，用于对应 $D$ 的子集 $D_v$
········其中 $D_v$ 表示 $D$ 中在 $a_{\ast }$ 上取值为 $a_{\ast }^v$ 的子集
········if ($D_v$ 为空)
········{
············令$C$是$D$中样本最多的分类
············node_child = “输出是$C$的叶节点”
········}
········else
········{
············node_child = TreeGenerate($D_v$, A ∖ { a x } A \setminus \{a_x\} A∖{ax​}) （其中\意思是从集合中去掉）
········}
····}
····return node
}

从上面算法可以看出，最关键步骤是： 从$A$中选择最优划分属性$a_{\ast }$

💠纯度（purity）

我们希望决策树的分支节点所包含的样本尽可能属于同一类别，即节点的“纯度”越来越高。

💠信息熵（information entropy）

“信息熵” 是度量样本集合纯度最常用的一种指标。
在样本集合 $D$ 中，用 $p_k(k=1,2,...,|\mathcal{Y}|)$ 表第 $k$ 类样本所占的比例。则 $D$ 的信息熵定义为：
$$\begin{gathered} Ent(D)=-\sum _{k=1}^{|\mathcal{Y}|}{p}_k{\log }_2{p}_k \\ (约定当p=0时，p{\log }_{2}p=0) \end{gathered}$$

$Ent(D)$ 越小，则 $D$ 的纯度越高

💠信息增益（information gain）

假定离散属性 $a$ 有 $V$ 个可能的取值 { a 1 , a 2 , . . . , a V } \{a^1,a^2,...,a^V\} {a1,a2,...,aV}。

若使用 $a$ 对样本集 $D$ 进行划分，则会产生 $V$ 个分支节点，其中第 $v$ 个分支节点包含了 $D$ 里所有在 $a$ 上取值为 $a^v$ 的样本，这个子集记为 $D_v$。

可以算出它们各自的信息熵$Ent(D_v)$。又因为每个分支节点所包含的样本数目不同，所以再乘算上权重 $\frac{|D^v|}{|D|}$。

最终，就可以计算出当使用 $a$ 对样本集 $D$ 进行划分时，所获得的 “信息增益”：
$$Gain(D,a)=Ent(D)-\sum _{v=1}^V\frac{|D^v|}{|D|}Ent(D_v)$$

信息增益越大，则表示用 $a$ 来进行划分所获得的纯度提升越大。所以在之前算法里 “从$A$中选择最优划分属性$a_{\ast }$” 的步骤中就可以选择纯度提升最大的 $a$。著名的 ID3 决策树学习算法[Quinlan,1986] 就是以此为准则来选择划分的属性。

💠增益率（gain ratio）

实际上，“信息增益” 的准则对可取值数目较多的属性有偏好。为减少此不利影响，可以使用“增益率”，定义为：
$$\begin{gathered} Gain\_raio(D,a)=\frac{Gain(D,a)}{IV(a)} \\ 其中：IV(a)=-\sum _{v=1}^V\frac{|D^v|}{|D|}{\log }_2\frac{|D^v|}{|D|} \end{gathered}$$

$IV(a)$ 被称为属性 $a$ 的“固有值(intrinsic value)”，通常属性取值数目越多（$V$越大）则 $IV(a)$ 越大。

但需要注意，“增益率” 的准则对可能取值数目较少的属性有所偏好。C4.5 算法使用了一个启发式[Quinlan,1993]：先找出信息增益高于平均水平的属性，然后再从中选择增益率最高的。

💠基尼指数（Gini index）

数据集 $D$ 的纯度可用“基尼值”来度量：
$$\begin{array}{rl}Gini(D)& =\sum _{k=1}^{|\mathcal{Y}|}\sum _{k^{\prime }\ne k}{p}_k{p}_{k^{\prime }}\\ & =1-\sum _{k=1}^{|\mathcal{Y}|}{p_k}^2\end{array}$$

直观来说 $Gini(D)$ 反映了从数据集 $D$ 中随机抽取两个样本，其类别标记不一致的概率。因此 $Gini(D)$ 越小，数据集 $D$ 纯度越高。

类似，属性 $a$ 的 基尼指数(Gini index) 定义为：
$$Gini\_index(D,a)=\sum _{v=1}^V\frac{|D^v|}{|D|}Gini(D_v)$$

于是，在侯选属性集合 $A$ 中，我们选择划分后基尼系数最小的属性。

💠剪枝（pruning）

决策树学习有时会出现决策树分支过多，也就是 “过拟合” 的情况。
剪枝（pruning）是决策树学习中对付 “过拟合” 的主要手段。

💠预剪枝（prepruning）

在决策树生成过程中，对每个节点在划分前先进行估计，如果不能带来泛化性提升，则停止划分并直接标记为叶节点。

优点：

• 减少训练开销。

缺点：

• 欠拟合风险。

💠后剪枝（post-pruning）

先生成一颗完整的决策树，然后自底向上地对非叶节点进行考察。若将该节点对应地子树替换为叶节点可以带来泛化性提升，则替换为叶节点。

优点：

• 欠拟合风险很小。泛化性能往往优于预剪枝。

缺点：

• 训练时间要大很多。

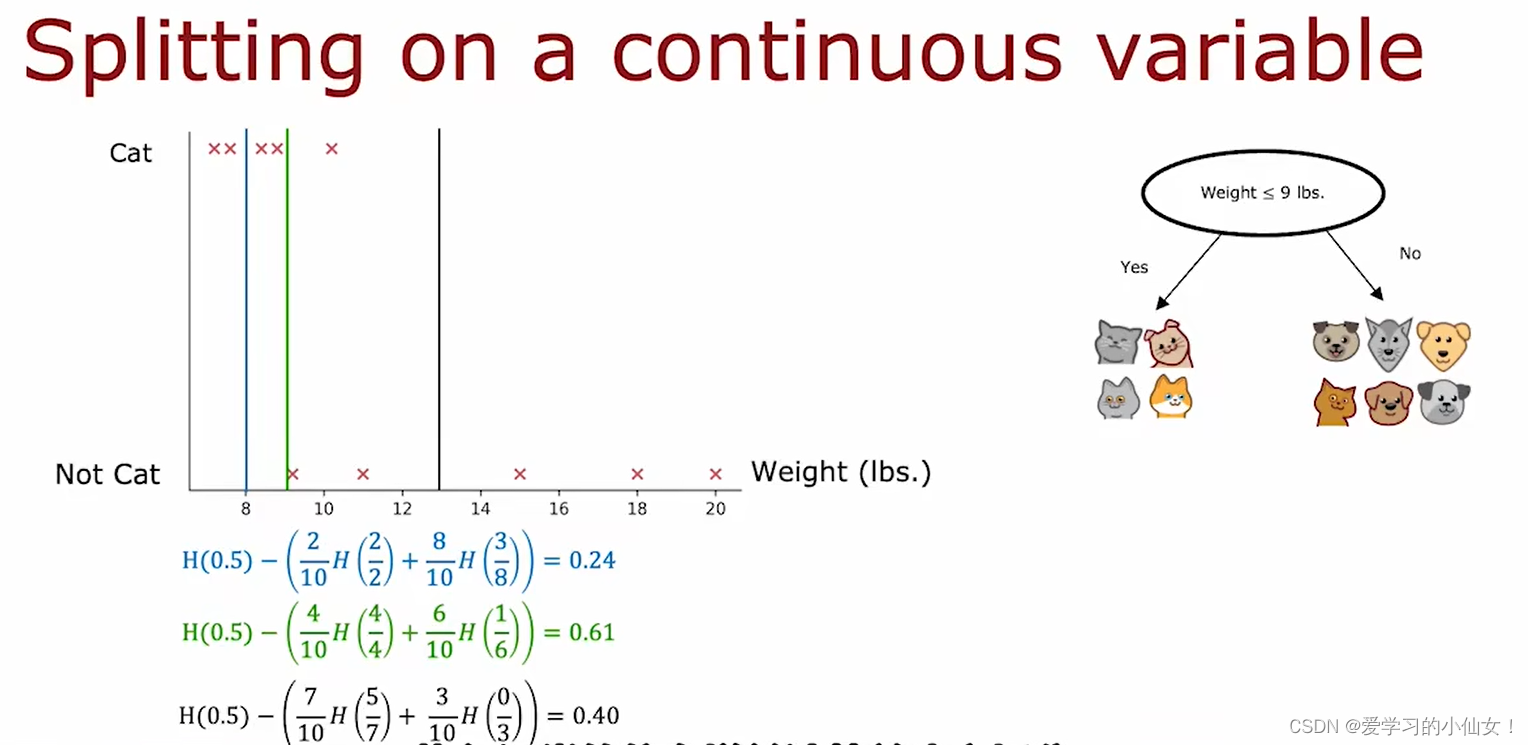
💠连续值处理：二分法(bi-partition)

当属性是连续值时，由于可取值的数目不再有限，因此无法再根据这个属性对节点进行划分。
此时可以用 “离散化技术”。最简单的策略是 二分法，C4.5决策树算法中采用了这个机制。

给定样本集 $D$ 和连续属性 $a$ 。假定 $a$ 在 $D$ 上出现了 $n$ 个不同的取值，将这些值从小到大进行排序，记为 { a 1 , a 2 , . . . , a n } \{a^1,a^2,...,a^n\} {a1,a2,...,an}。基于划分点 $t$ 可将 $D$ 划分为子集 $D_t^{-}$ 和 $D_t^{+}$，分别表示哪些在属性 $a$ 上 “不大于$t$” 和 “大于$t$”的样本。显然，$t$ 在区间 $[a^i,a^{i+1})$ 中取任意值的划分结果相同。因此，我们考察的候选划分点集合：
T a = { a i + a i + 1 2 ∣ 1 ⩽ i ⩽ n − 1 } T_a=\{\frac{a^i+a^{i+1}}{2}|1\leqslant i\leqslant n-1\} Ta​={2ai+ai+1​∣1⩽i⩽n−1}
随后，就可以像离散属性值一样考察这些划分点，选出最优的划分点对样本集合进行划分了。

需要注意，不同于离散属性，若当前节点划分属性为连续属性，后续节点仍旧可以用这个属性进行划分。

💠缺失值处理

样本的某些属性可能出现缺失，如果简单放弃不完整的样本，显然是对数据信息极大的浪费。

考虑有缺失值的训练样本进行学习，需要解决两个问题：

（问题1）如何选择用于划分的属性？

给定训练集 $D$ 和属性 $a$。$a$ 有 $V$ 个可能的取值 { a 1 , a 2 , . . . , a V } \{a^1,a^2,...,a^V\} {a1,a2,...,aV}。分类取值为$(k=1,2,...,|\mathcal{Y}|)$。令：
$\tilde{D}$ 表示 $D$ 在 $a$ 上没有缺失值的样本子集。
${\tilde{D}}^v$ 表示 $\tilde{D}$ 在 $a$ 上取值为 $a^v$ 的子集。
${\tilde{D}}_k$ 表示 $\tilde{D}$ 属于 $k$ 类的子集。

假定每个样本$\mathbf{x}$都有一个权重 ${\omega }_{\mathbf{x}}$。然后定义：
$\rho$ 表示无缺失值样本所占的比例，即：$\rho =\frac{{\sum }_{\mathbf{x}\in \tilde{D}}{\omega }_{\mathbf{x}}}{{\sum }_{\mathbf{x}\in D}{\omega }_{\mathbf{x}}}$
${\tilde{p}}_k$表示无缺失值样本中第 $k$ 类所占的比例，即${\tilde{p}}_k=\frac{{\sum }_{\mathbf{x}\in {\tilde{D}}_k}{\omega }_{\mathbf{x}}}{{\sum }_{\mathbf{x}\in \tilde{D}}{\omega }_{\mathbf{x}}}$
${\tilde{r}}_v$表示无缺失值样本中在属性 $a$ 上取值为 $a^v$ 的样本所占的比例，即${\tilde{r}}_v=\frac{{\sum }_{\mathbf{x}\in {\tilde{D}}^v}{\omega }_{\mathbf{x}}}{{\sum }_{\mathbf{x}\in \tilde{D}}{\omega }_{\mathbf{x}}}$

基于上述定义，用属性 $a$ 进行划分的信息增益的计算公式推广为：
$$\begin{gathered} \begin{array}{rl}Gain(D,a)& =\rho \times Gain(\tilde{D},a)\\ & =\rho \times (Ent(\tilde{D})-\sum _{v=1}^V{\tilde{r}}_{v}Ent({\tilde{D}}^v))\end{array} \\ 其中：Ent({\tilde{D}}^v)=-\sum _{k=1}^{|\mathcal{Y}|}{\tilde{p}}_k{\log }_2{\tilde{p}}_k \end{gathered}$$

接着就可以正常计算出用哪个属性进行划分最好了

（问题2）若样本在该属性上缺失，则应该划分到哪个分支节点？
采用以下逻辑：

• 假如样本 $\mathbf{x}$ 在属性 $a$ 上已知，则正常划分到对应分支节点，权重值保持为 ${\omega }_{\mathbf{x}}$。
• 假如样本 $\mathbf{x}$ 在属性 $a$ 上缺失，则将 $\mathbf{x}$ 划分到所有的分支节点，并将 $a^v$ 对应的分支节点中的权重值调整为 ${\tilde{r}}_v\cdot {\omega }_{\mathbf{x}}$。

💠多变量决策树

上面所讨论的都是单变量的决策树，也就是每个分支节点都使用一个属性进行划分。

若我们把每个属性视为坐标空间中的一个坐标轴，则 $d$ 个属性描述的样本就对应了 $d$ 维空间中的一个点。对样本分类意味着在这个空间中寻找不同样本间的分类边界。单变量的决策树所形成的分类边界的特点是：分类边界是与坐标轴平行的（axis-parallel）。举例：

左图是决策树，右侧是其对应的分类边界：

但是，当学习任务的真实分类边界 比较复杂时，必须使用很多段划分才能获得较好的近似，如下图：

其中绿线是真实的分类边界。
此时如果还使用单变量的决策树，则会需要很多分段。可以看到黑线有9段。
但如果使用多变量的决策树，则只需要3段。红线代表使用多变量决策树的分类边界。

在多变量决策树中，每个分支节点不再是针对于一个属性，而是对属性的线性组合进行测试，即每个分支节点都是一个形如 ${\sum }_{i=1}^d{\omega }_i{a}_i=t$ 的线性分类器，其中 ${\omega }_i$ 是 $a_i$ 的权重，${\omega }_i$ 和 $t$ 都是学习所得。

这样，对于之前的样本，学习成多变量决策树如左图，对应的分类边界如右图：