算法之最短路径算法
最短路径算法
概念:
考查最短路径问题,可能会输入一个赋权图(也就是边带有权的图),则一条路径的v1v2…vN的值就是对路径的边的权求和,这叫做赋权路径长,如果是无权路径长就是单纯的路径上的边数。
在赋权图,可能会出现负值边的情况,这样当我们去找最短路径时,可能会产生负值圈,毕竟一直走负值边可以将数值变得更短。
单源最短路径问题:
- 给定一个赋权图G=(V,E)和一个特定顶点s作为输入,找出从s到G中每一个其他顶点的最短赋权路径。
无权最短路径:
- 给定一个无权图G=(V,E)和一个起始顶点s作为输入,找出从s到G中每一个其他顶点的最短路径。
广度优先搜索算法(BFS)
概念:
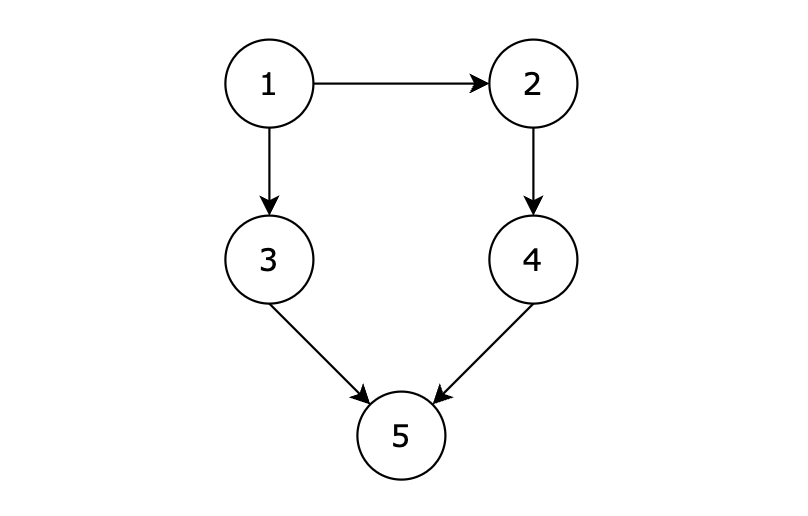
- 广度优先搜索算法(BFS)用于在无权图或者边权相同的图中寻找最短路径。
- 该方法按层处理顶点,首先从起始点出发,进行发散找到与起始点邻接的顶点a,…,并将s到这些顶点的路径距离更新,然后将该点标记成已经访问的顶点并将该点的前一个顶点记录下来(被标记的顶点我们后面遇到就认为该点已经不需要再进行处理了),然后再从顶点a,…发散,找到该顶点的邻接顶点,然后重复操作,直到所有顶点都被标记完,就完成了搜索。
- 具体代码实现,是用一个队列,在迭代开始时,队列中只含有距离为迭代距离currdist的那些顶点,然后执行操作时,将距离currdist+1的顶点的那些顶点添加到队列中,只要当前距离为currdist顶点处理完,就会处理距离为currdist+1(也就是当前顶点发散的顶点)的顶点添加到队列中。
- 在队列中其实可以将know域也就是标记去掉,因为队列的形式已经说明执行过了,就不会在执行,因此相当于标记了。
代码:
//图的邻接表的结点信息
struct listnode{
int data;
bool flag; //判断是否访问过
int path; //存储上一个顶点
int dist; //距离
listnode* next;
};
//图的信息
class graph{
private:
listnode *an; //邻接表形式存储图
int vnum; //图中结点数
};
//s为起点,an数组的邻接表表示图
void BFS(int s){
queue<int>q;
q.push(s);
an[s].dist=0;
while (!q.empty()){
int v=q.front();
q.pop();
an[v].flag= true;
listnode* p=an[v].next;
while (p!= nullptr){
if(an[p->data].dist==INT_MAX){
an[p->data].dist=an[v].dist+1;
an[p->data].path=v;
q.push(p->data);
}
p=p->next;
}
}
}
Dijkstra算法
概念:
- 用于求解赋权图的最短路径(无负值边),Dijkstra算法是解决单源最短路径问题的一般方法,并且该解法是贪心算法。Dijkstra只是BFS的升级版使他能够求赋权图的最短路径,如果求无权图Dijkstra跟BFS的做法一样!
- Dijkstra算法是分阶段的,该算法认为每一个阶段,都将该阶段当作最好的情况处理,类似于BFS算法,但是还是有不同的地方,比起BFS多出了需要进行每个阶段出现最好情况就进行更新路径。
- 具体做法是,从图中选取起始点v,然后找出邻接点,并将当前起始点到邻接点v3,v4…的距离更新,如果是赋权图就是dv+Cv,v3(就是顶点v到v3的权),如果是无权就是dv+1,并将v标记为已知。然后选取邻接点集中的一点再做为起始点,然后重复操作,将当前顶点的前一个顶点记录。当v到某个顶点的距离在当前阶段是最小的(最好情况),那么就进行更新,如果不是就无需更新。
- 具体来说,当我们扩展一个新结点时,我们会考虑它的所有未访问过的邻接结点,并计算从起始结点经过当前结点到达邻接结点的路径长度。如果这个长度小于已知的最短路径长度(或者邻接结点的路径长度尚未初始化),我们就更新邻接结点的路径长度。这样做的目的是通过不断更新路径长度来找到起始结点到所有其他结点的最短路径。
- 实现的时候可以使用优先队列来进行优化算法,只将顶点和其最短路径值进入队列中当队列非空,执行以下操作:u等于队顶的节点,w等于队顶节点的最短路径值;遍历u的所有边,如果能找到节点v最短路径值小于v的当前值,更新v,将v压入队列。结束
- 没有用优先队列优化的Dijkstra算法的时间复杂度为O(N²),如果使用优先队列,则时间复杂度为O(nlogn),可以不用考虑已知域;
Dijkstra跟BFS区别:
- 处理顶点:
- 在BFS算法中,当一个顶点被扩展时,它的所有未访问过的邻居顶点都被添加到队列中,这样它们将按照遍历的顺序逐个被访问。
- 在Dijkstra算法中,当一个顶点被扩展时,它的邻居顶点也被考虑,但是Dijkstra算法会计算扩展的顶点与其邻居之间的边的权重,并根据这个权重来更新到达邻居顶点的最短路径长度。这个更新过程使得Dijkstra算法能够处理带有非负权重的图。
- 选择下一个顶点:
- 在BFS算法中,下一个要被扩展的顶点是队列中的下一个顶点,也就是按照队列的先进先出(FIFO)原则选择。
- 在Dijkstra算法中,下一个要被扩展的顶点是距离起始点路径长度最小的顶点,也就是根据已知的最短路径长度来选择。这需要使用优先队列或者最小堆来高效地选择路径长度最小的顶点。
代码:
//图的邻接表的结点信息
struct listnode{
int data;
int path; //存储上一个顶点
int dist; //最短距离
int weight; //数组索引顶点跟该顶点的边的权重
listnode* next;
};
//图的信息
class graph{
private:
listnode *an; //邻接表形式存储图
int vnum; //图中结点数
};
//v是起始点
void Dijkstra(int v){
an[v].dist=0;
queue<int>q;
q.push(v);
while (!q.empty()){
int w=q.front();
q.pop();
listnode* p=an[w].next;
while (p!= nullptr){
if(an[w].dist+p->weight<an[p->data].dist){
an[p->data].dist=an[w].dist+p->weight;
an[p->data].path=w;
q.push(p->data);
}
p=p->next;
}
}
}
题目模板:
有向边单源最短路径问题
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int N=10;
int n;
struct edge {
int v, w;
};
bool vis[N+1];
int dijkstra(int start, const vector<vector<edge>>& graph) {
int minroad[n+1];
memset(minroad,INF,sizeof minroad);
minroad[start] = 0;
priority_queue<pair<int, int>, vector<pair<int, int>>, greater<pair<int, int>>> pq;
pq.push({0, start});
while (!pq.empty()) {
auto [d, u] = pq.top();
pq.pop();
if(vis[u]) continue;
vis[u]=true;
for (const auto& edges : graph[u]) {
int v = edges.v;
int w = edges.w;
if (minroad[u] + w < minroad[v]) {
minroad[v] = minroad[u] + w;
pq.push({minroad[v], v});
}
}
}
return minroad[n]!=INF?minroad[n]:-1;
}
int main() {
int m, start;
cin >> n >> m >> start;
vector<vector<edge>> graph(n + 1);
for (int i = 0; i < m; i++) {
int u, v, w;
cin >> u >> v >> w;
graph[u].push_back({v, w});
}
cout<<dijkstra(start, graph)<<endl;
system("pause");
return 0;
}
Floyd算法
概念:
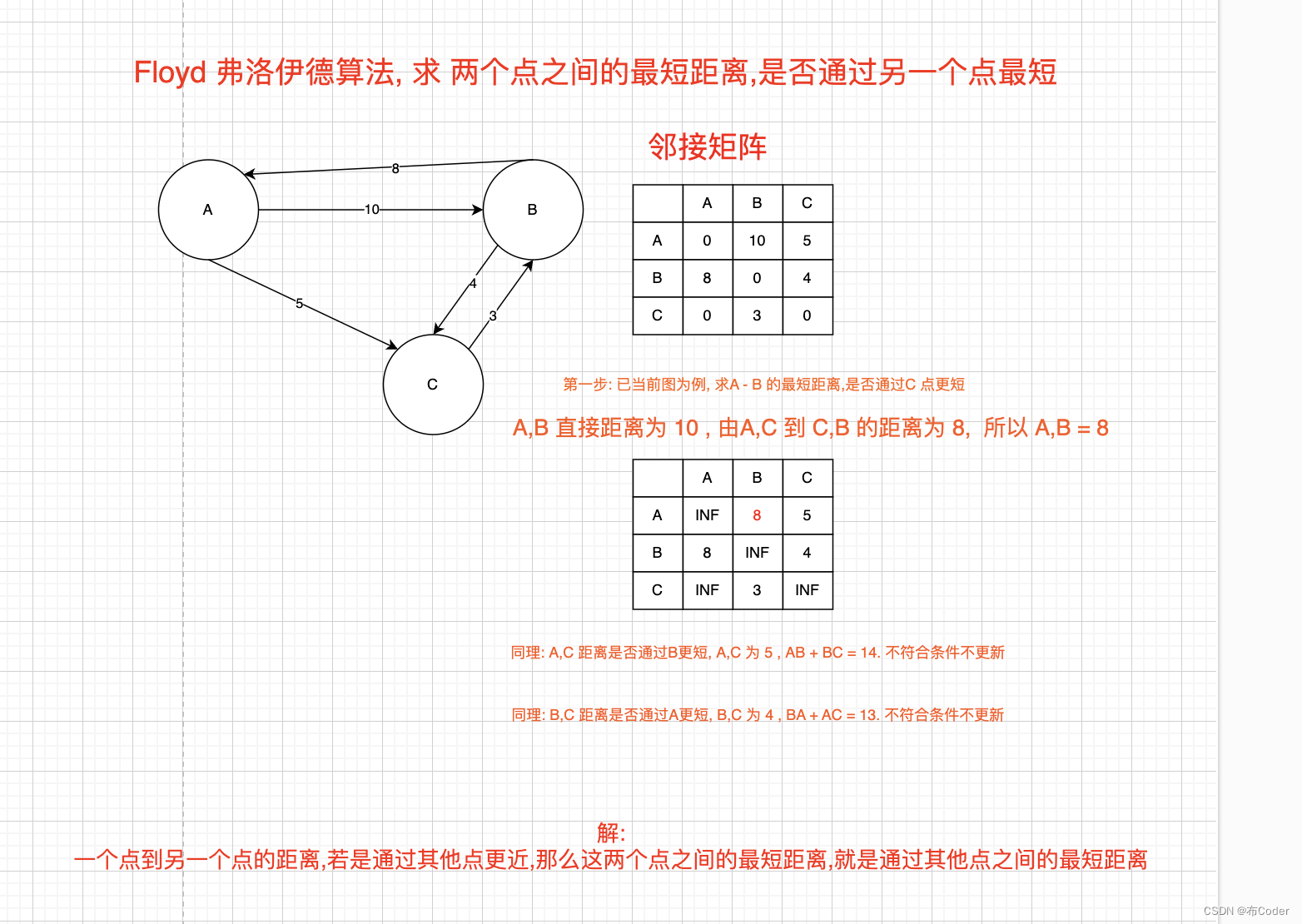
- Floyd(弗洛伊德)算法是基于动态规划思想的算法,也称插点法,是全源最短路算法(全源就代表经过一次Floyd算法,每个点到各个点的最短路径都能算出来)
- 用于求任意一对顶点间的最短路径,此时图中的边的权值可以出现负数,但不能出现负环
- 时间复杂度为
O(n³),n为点个数
基本思想:
- 对于从i到j的弧,进行n次试探
- 首先考虑i,0,j是否存在,如果存在,则比较i,j和i,0,j的路径长度,去最短者进行更新i,j的最短路径
- 然后再添加顶点1,依次类推。
具体过程:
- 当一个图里有n个城市,求全源最短路径问题
- 定义城市k为从当前图拿出来,并重新插入图中的城市,
城市i,城市j分别为当前源城市和目的城市。dist[i\][j]表示城市i到城市j的最短路径 - 假设当前图中没有城市k,我们将城市k重新插入到图中
- 我们需要判断城市i到城市j的最短路径是否要更新,则比较路径经过城市k和原来的路径长度进行比较,如果经过城市k的路径长度更短,则更新dist[i][j],因此就为
dist[i][j]=min(dist[i][k]+dist[k][j],dist[i][j]) - 因此对这个图执行n次上述操作(也就是插点法),得出的dist二维数组就为全源的最短路径。
代码模板:
//dist[n][n]用来记录图中各点到各点的最短路径
void Floyd(int **dist){
for(int k=0;k<n;++k){
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
if(dist[i][k]+dist[k][j]<dist[i][j]){
dist[i][j]=dist[i][k]+dist[k][j];
}
}
}
}
}
例题部分代码:
具体可看力扣1334. 阈值距离内邻居最少的城市,只包含求解全源最短路径代码
#include <iostream>
#include <cstring>
#include <vector>
using namespace std;
void Floyd(int n, vector<vector<int>>& edges){
const int INF=0x3f3f3f3f;
int dist[n][n];
memset(dist,INF, sizeof(dist));
for(int i=0;i<n;++i){
dist[i][i]=0;
}
for(auto edge:edges){
dist[edge[0]][edge[1]]=edge[2];
dist[edge[1]][edge[0]]=edge[2];
}
//Floyd算法计算全源最短路代码
for(int k=0;k<n;++k){
for(int i=0;i<n;++i){
for(int j=0;j<n;++j){
if(dist[i][k]+dist[k][j]<dist[i][j]){
dist[i][j]=dist[i][k]+dist[k][j];
}
}
}
}
for(int i=0;i<n;++i){
cout<<"第"<<i<<"城市到其他城市最短路径:";
for(int j=0;j<n;++j)
cout<<"("<<i<<","<<j<<","<<dist[i][j]<<")"<<" ";
cout<<endl;
}
}
int main() {
vector<vector<int>>edges{{0,1,2},{0,4,8},{1,2,3},{1,4,2},{2,3,1},{3,4,1}};
Floyd(5,edges);
system("pause");
return 0;
}
尾言
完整版笔记也就是数据结构与算法专栏完整版可到我的博客进行查看,或者在github库中自取(包含源代码)
- 博客1: codebooks.xyz
- 博客2:moonfordream.github.io
- github项目地址:Data-Structure-and-Algorithms