SVM支持向量机

SVM的由来和概念

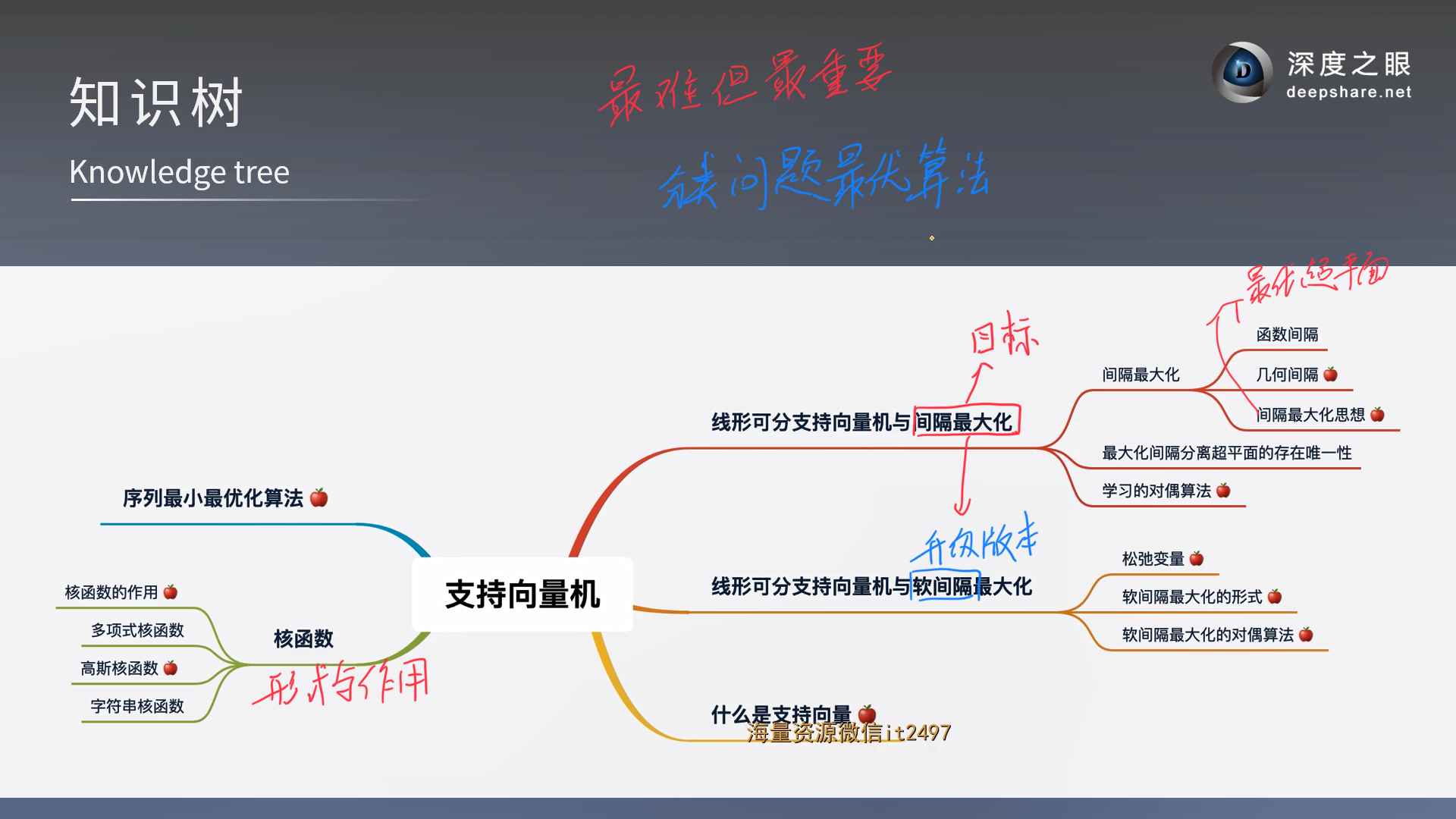
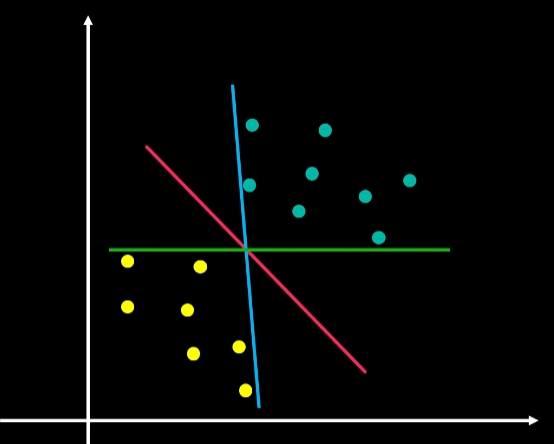
间隔最大化是找最近的那个点的距离’

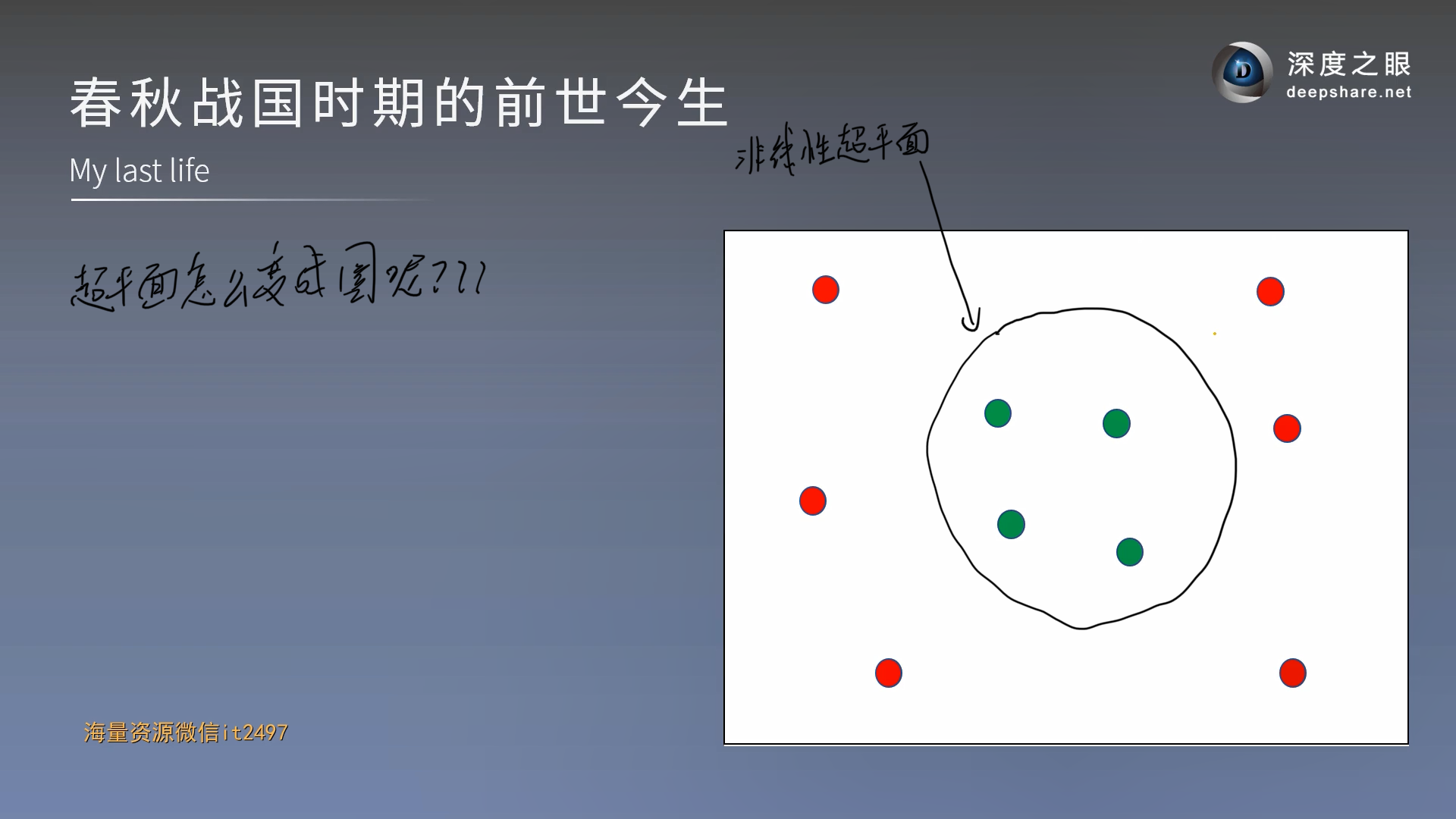
之前我们学习的都是线性超平面,现在我们要将超平面变成圈

对于非线性问题升维来解决

对于下图很难处理,我们可以将棍子立起来,然后说不定red跑到左边了,green跑到右边了(可能增加了某种筛选条件导致两个豆子分离)(只是一种比喻)

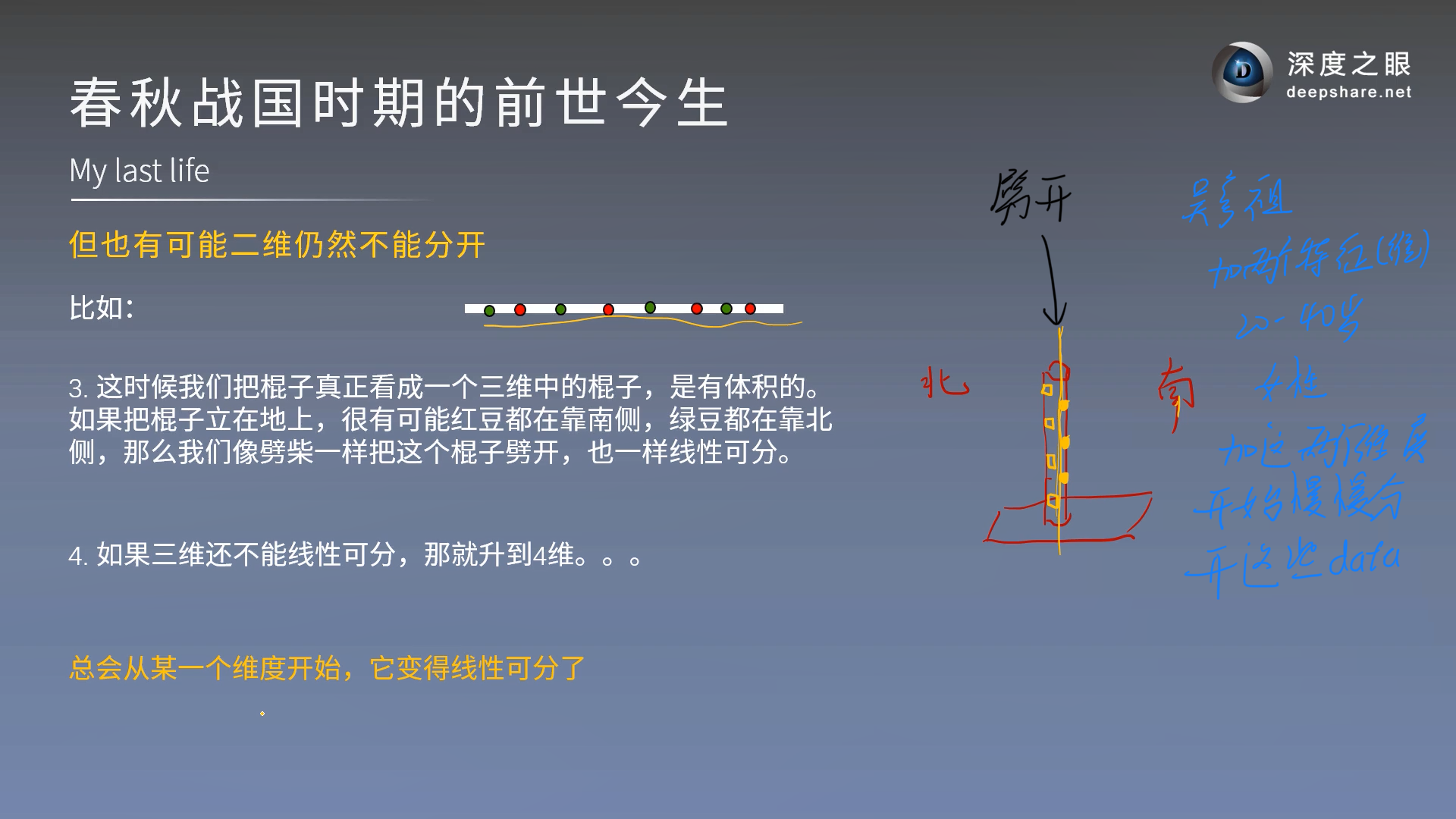
打个比方,要把刀哥和吴彦祖分开,豆子代表人们,加上几个特征(维度)1.20-40岁 2.女性 就可以大致将人们分的差不多了,可以继续加特征(维度)来使其更加分离

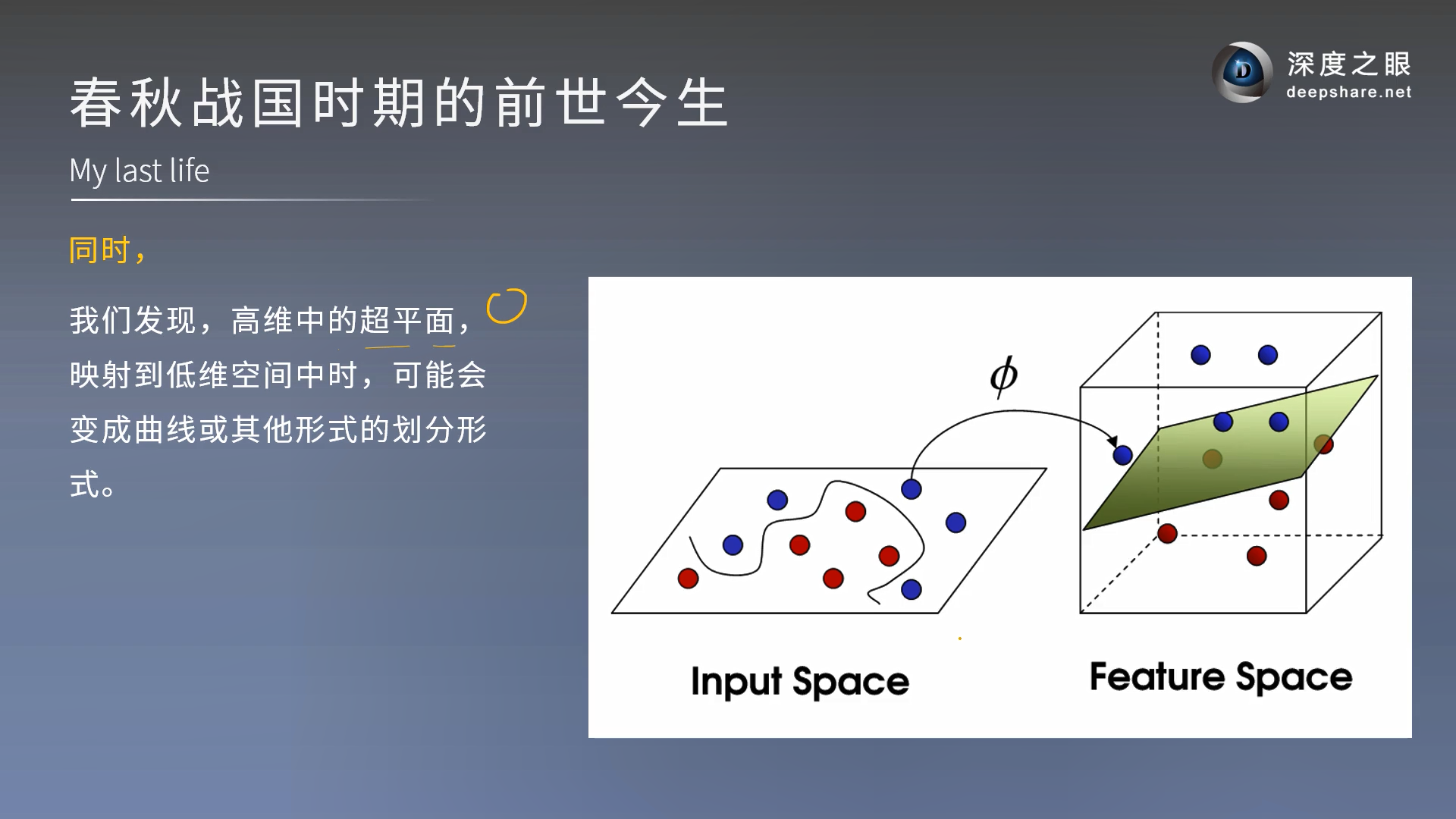
SVM本质还是非线性的,只是为了更好理解所以我们说在更高维是线性的

已经分开了,在再加特征(维度),相当于如虎添翼

复习函数间隔和几何间隔

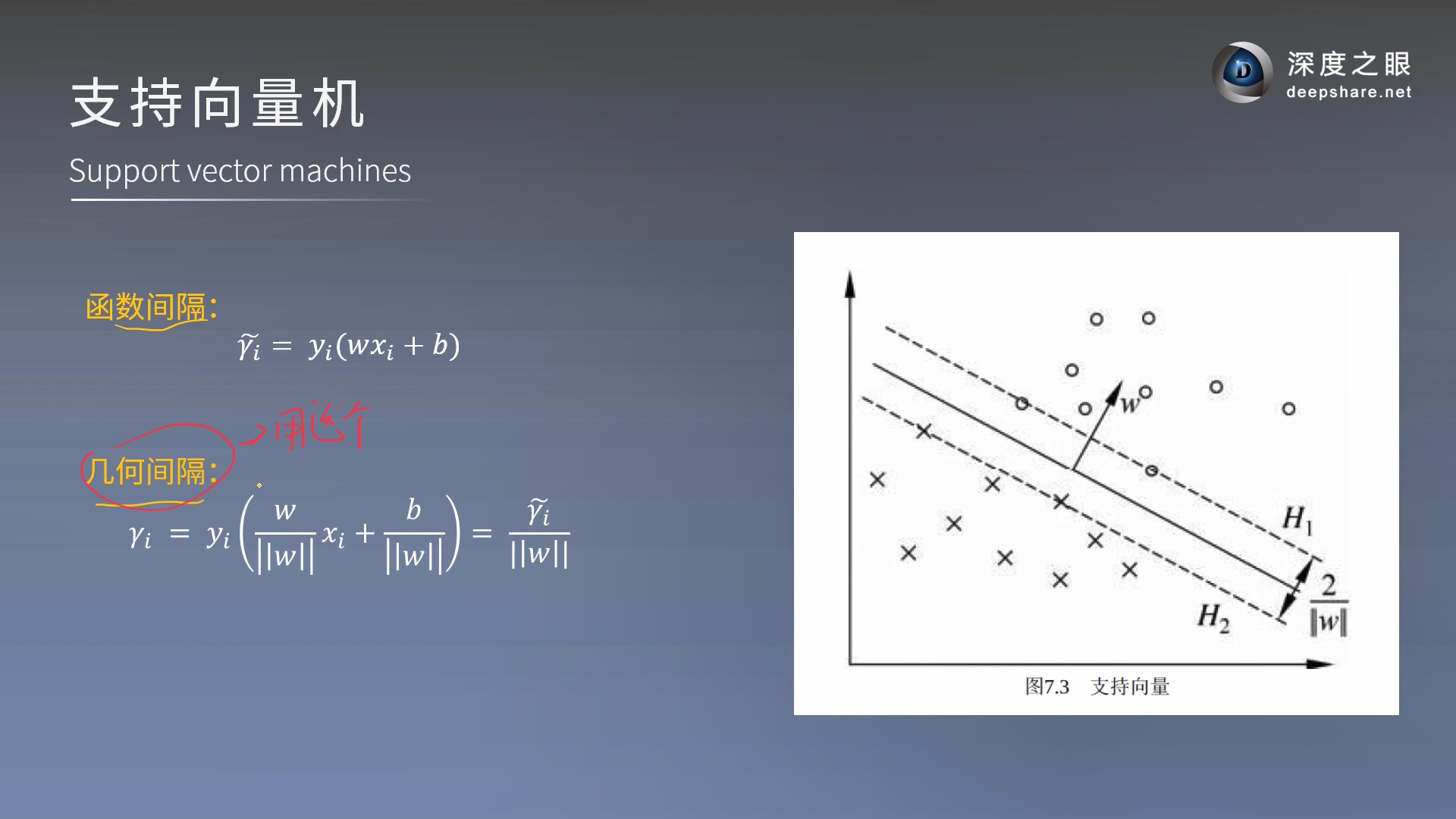
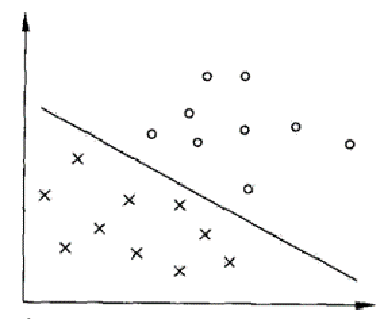
pure线性分类器

$$\gamma$$指的是几何间隔,是不会变的间隔,$${\gamma }^{{}^{\prime }}$$是函数间隔,是可变的间隔,所以我们通过变换将要求的几何间隔变为求函数间隔$${\gamma }^{{}^{\prime }}$$,然后函数间隔可以等比例放大缩小,所以可以将其等比例放大缩小为1

对于$${\gamma }^{{}^{\prime }}$$和$$\gamma$$指的是间隔最大化的距离(也就是说某一个点)

此时此刻我们将函数间隔等比例放大缩小为了1,所以是求max$$\frac{1}{||w||}$$,条件就是$$s.t{y}_i(w^T{x}_i+b)\ge 1(i=1,2,...m)$$,要求那个最大值,我们可以等价转换求$$min\frac{1}{2}||w|{|}_2^2$$(高数拉格朗日的原理不能忘记)

下面列拉格朗日乘子法列的式子

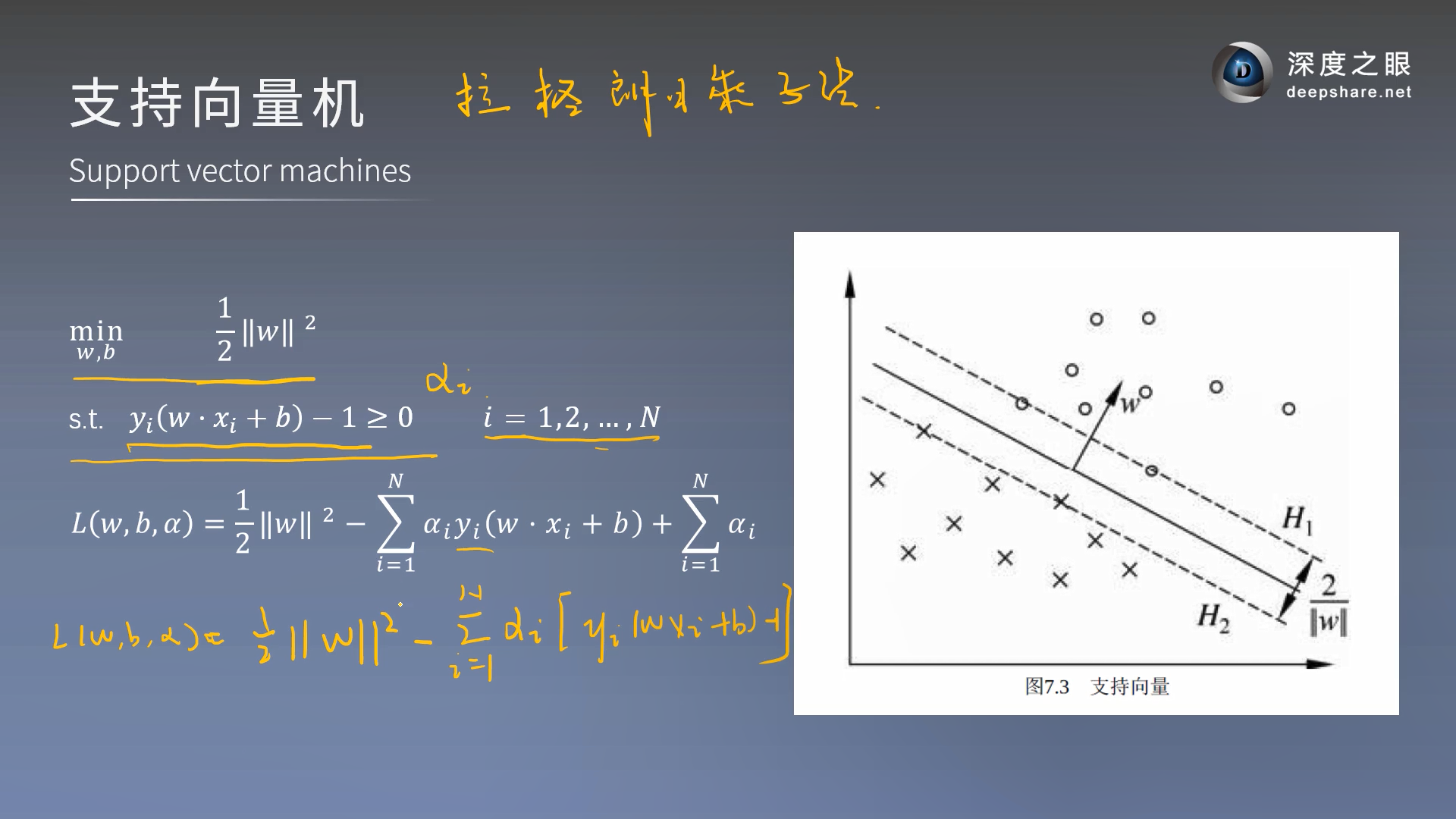
$${\alpha }_i$$就是拉格朗日乘子法里面设的未知数

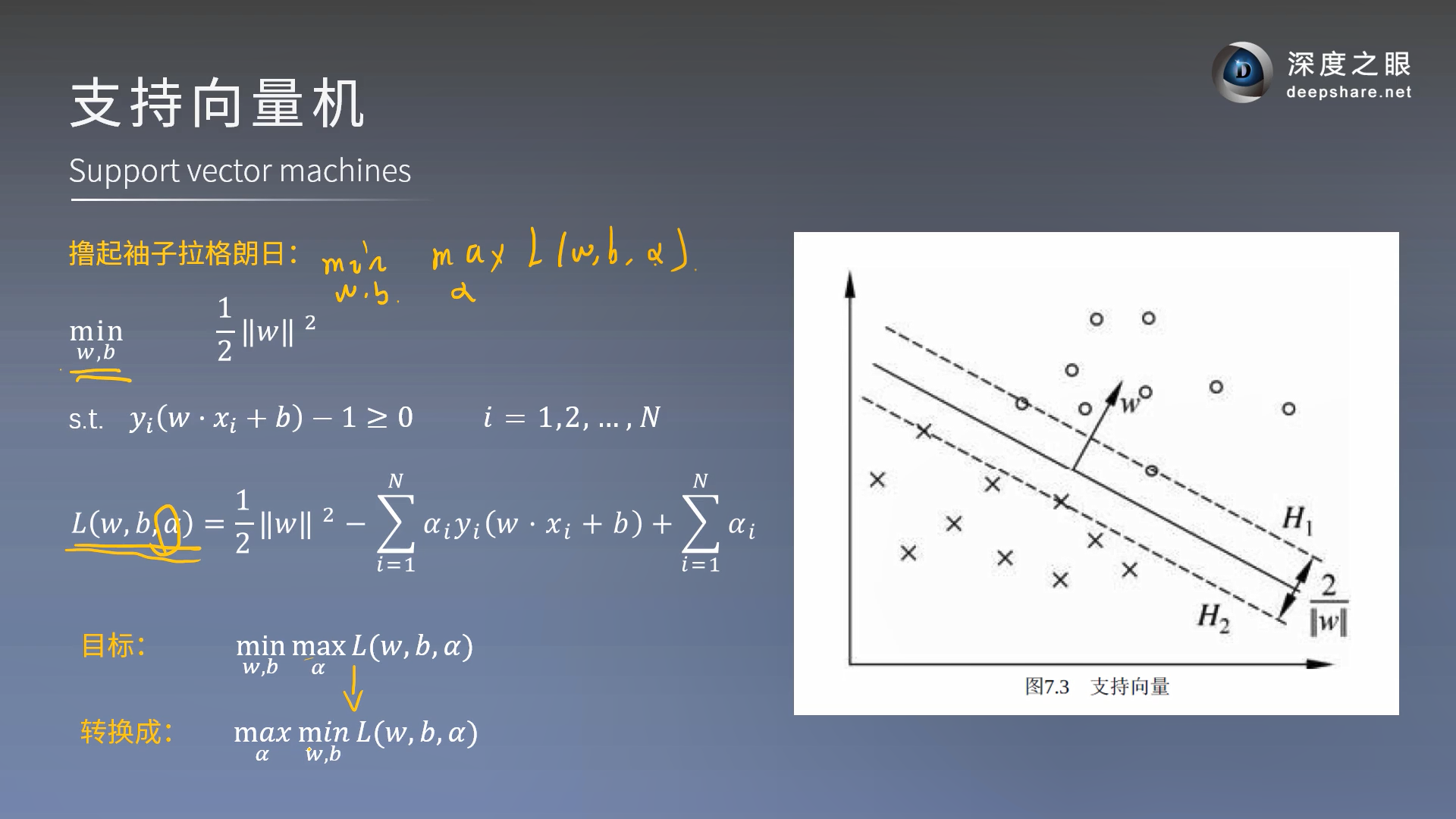
转换为求这个的对偶问题(后面的有些操作和最大熵式子的推导及其类似)]

分别对w和b求导得到上面两个式子,将这两个式子带入$$L(w,b,\alpha )$$

化简过程如下

dodo老师的化简过程

$$\underset{{\alpha }_i\ge 0}{\underbrace{max}}\underset{w,b}{\underbrace{min}}L(w,b,\alpha )$$

求完了第一层的min接下来求第二层的max,求这个最大值

第二层的max的求法暂且不表,后面有方法来求

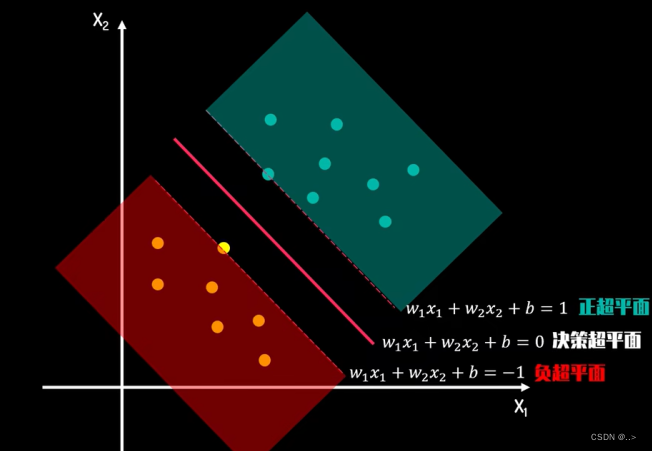
软间隔线性分类器

给入松弛变量,允许小部分进入边界(小部分误差)

当然，松弛变量不能白加，这是有成本的，每一个松弛变量${\xi }_i$, 对应了一个代价${\xi }_i$，这个就得到了我们的软间隔最大化的SVM学习条件如下：

$$min\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\xi }_i$$

$$s.t.y_i(w^T{x}_i+b)\ge 1-{\xi }_i(i=1,2,...m)$$

$${\xi }_i\ge 0(i=1,2,...m)$$

这里,C>0为惩罚参数，可以理解为我们一般回归和分类问题正则化时候的参数。C越大，对误分类的惩罚越大，C越小，对误分类的惩罚越小。

也就是说，我们希望$\frac{1}{2}||w|{|}_2^2$尽量小，误分类的点尽可能的少。C是协调两者关系的正则化惩罚系数。在实际应用中，需要调参来选择。

我们要求这个几何间隔的最大值和前面pure线性分类器类似

$$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1+{\xi }_i]-\sum _{i=1}^m{\mu }_i{\xi }_i$$

其中${\mu }_i\ge 0,{\alpha }_i\ge 0$,均为拉格朗日系数。

也就是说，我们现在要优化的目标函数是：

$$\underset{w,b,\xi }{\underbrace{min}}\underset{{\alpha }_i\ge 0,{\mu }_i\ge 0,}{\underbrace{max}}L(w,b,\alpha ,\xi ,\mu )$$

这个优化目标也满足KKT条件，也就是说，我们可以通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解如下：

$$\underset{{\alpha }_i\ge 0,{\mu }_i\ge 0,}{\underbrace{max}}\underset{w,b,\xi }{\underbrace{min}}L(w,b,\alpha ,\xi ,\mu )$$

我们可以先求优化函数对于w,b的极小值, 接着再求拉格朗日乘子α和 μ的极大值。

首先我们来求优化函数对于w,b,ξ的极小值，这个可以通过求偏导数求得：

$$\frac{\partial L}{\partial w}=0\Rightarrow w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$$

$$\frac{\partial L}{\partial b}=0\Rightarrow \sum _{i=1}^m{\alpha }_i{y}_i=0$$

$$\frac{\partial L}{\partial \xi }=0\Rightarrow C-{\alpha }_i-{\mu }_i=0$$

然后利用这个式子消除w和b

$$\begin{array}{rl}L(w,b,\xi ,\alpha ,\mu )& =\frac{1}{2}||w|{|}_2^2+C\sum _{i=1}^m{\xi }_i-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1+{\xi }_i]-\sum _{i=1}^m{\mu }_i{\xi }_i\\ & =\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1+{\xi }_i]+\sum _{i=1}^m{\alpha }_i{\xi }_i\\ & =\frac{1}{2}||w|{|}_2^2-\sum _{i=1}^m{\alpha }_i[y_i(w^T{x}_i+b)-1]\\ & =\frac{1}{2}{w}^{T}w-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i\\ & =\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-\sum _{i=1}^m{\alpha }_i{y}_i{w}^T{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i\\ & =\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-w^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-\sum _{i=1}^m{\alpha }_i{y}_{i}b+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}{w}^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-b\sum _{i=1}^m{\alpha }_i{y}_i+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i{)}^T(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i)-b\sum _{i=1}^m{\alpha }_i{y}_i+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i-b\sum _{i=1}^m{\alpha }_i{y}_i+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T\sum _{i=1}^m{\alpha }_i{y}_i{x}_i+\sum _{i=1}^m{\alpha }_i\\ & =-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{y}_i{x}_i^T{\alpha }_j{y}_j{x}_j+\sum _{i=1}^m{\alpha }_i\\ & =\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j\end{array}$$

这个结果和pure线性分类器结果一样,唯一不一样的是约束条件

$$\underset{\alpha }{\underbrace{max}}\sum _{i=1}^m{\alpha }_i-\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$

$$C-{\alpha }_i-{\mu }_i=0$$

$${\alpha }_i\ge 0(i=1,2,...,m)$$

$${\mu }_i\ge 0(i=1,2,...,m)$$

对于$$C-{\alpha }_i-{\mu }_i=0，{\alpha }_i\ge 0，{\mu }_i\ge 0$$这3个式子,我们可以得到$$0\le {\alpha }_i\le C$$

$$\underset{\alpha }{\underbrace{min}}\frac{1}{2}\sum _{i=1,j=1}^m{\alpha }_i{\alpha }_j{y}_i{y}_j{x}_i^T{x}_j-\sum _{i=1}^m{\alpha }_i$$

$$s.t.\sum _{i=1}^m{\alpha }_i{y}_i=0$$\

$0\le {\alpha }_i\le C$和pure线性分类器比就多了这个约束条件,求$$\alpha$$和pure那个一样通过SMO算法来求上式极小化时对应的α向量就可以求出w和b了。

引入核函数

这里x是向量,怎么方便求向量的点积,需要引入核函数

幂函数好使

SMO

我们假设我们通过SMO算法求得了我们得到了对应的α的值${\alpha }^{\ast }$。

那么我们根据$w=\sum _{i=1}^m{\alpha }_i{y}_i{x}_i$,可以求出对应的w的值$w^{\ast }=\sum _{i=1}^m{\alpha }_i^{\ast }{y}_i{x}_i$

求b则稍微麻烦一点。注意到，对于任意支持向量$(x_x,y_s)$，都有

$$y_s(w^T{x}_s+b)=y_s(\sum _{i=1}^m{\alpha }_i{y}_i{x}_i^T{x}_s+b)=1$$(到超平面的函数距离人为设置为1)

假设我们有S个支持向量，则对应我们求出S个$b^{\ast }$,理论上这些$b^{\ast }$都可以作为最终的结果， 但是我们一般采用一种更健壮的办法，即求出所有支持向量所对应的$b_s^{\ast }$，然后将其平均值作为最后的结果。注意到对于严格线性可分的SVM，b的值是有唯一解的(那是肯定的,因为对于二维而言,支持向量到最优超平面之间的距离是一样的都是1)，也就是这里求出的所有$b^{\ast }$都是一样的，这里我们仍然这么写是为了和后面加入软间隔后的SVM的算法描述一致。

支持向量:和超平面平行的保持一定的函数距离的这两个超平面对应的向量(不是法向量),相当于A,B两点画平行线(支持向量),然后平行线之间的距离最大就是最优的超平面

(我们已经得到最优超平面的前提下,需要求支持向量)怎么得到支持向量呢？根据KKT条件中的对偶互补条件${\alpha }_i^{\ast }(y_i(w^T{x}_i+b)-1)=0$,如果${\alpha }_i>0$则有$y_i(w^T{x}_i+b)=1$即点在支持向量上，否则如果${\alpha }_i=0$(无约束条件问题),则有$y_i(w^T{x}_i+b)\ge 1$,即样本在支持向量上或者已经被正确分类。