以下内容为结合李沐老师的课程和教材补充的学习笔记,以及对课后练习的一些思考,自留回顾,也供同学之人交流参考。
本节课程地址:本节无视频课程
本节教材地址:4.7. 前向传播、反向传播和计算图 — 动手学深度学习 2.0.0 documentation (d2l.ai)
本节开源代码:...>d2l-zh>pytorch>chapter_multilayer-perceptrons>backprop.ipynb
本节教材内容推导详细,没有补充,直接跳到练习。
练习
- 假设一些标量函数
的输入
是
矩阵。
相对于
的梯度维数是多少?
解:
对于标量函数 相对于
的梯度,它的维度与
的维度相同,即
。每个元素 (𝑖,𝑗) 将表示
相对于
的第 𝑖 行第 𝑗 列元素的偏导数。
2. 向本节中描述的模型的隐藏层添加偏置项(不需要在正则化项中包含偏置项)。
a. 画出相应的计算图。
解:
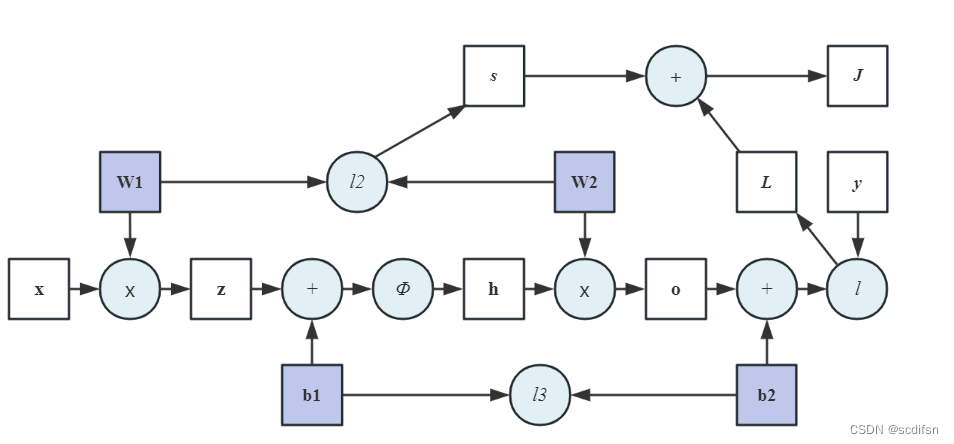
b. 推导正向和反向传播方程。
解:
正向传播:
反向传播:
3. 计算本节所描述的模型,用于训练和预测的内存占用。
解:
假设采用Fashion-MNIST数据集,单个隐藏层(256),输入784,输出10,wd为0.5,运行1个epoch,代码和比较结果如下(预测所用内存较小):
import torch
from torch import nn
import torch.optim as optim
import psutil
from d2l import torch as d2l
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
batch_size, lr, wd = 256, 0.1, 0.5
loss = nn.CrossEntropyLoss(reduction='none')
trainer = torch.optim.SGD([
{"params":net[1].weight,'weight_decay': wd},
{"params":net[1].bias},
{"params":net[3].weight,'weight_decay': wd},
{"params":net[3].bias}], lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
# 计算模型参数的内存占用
# 以MB为单位(/(1024**2))
d2l.train_epoch_ch3(net, train_iter, loss, trainer)
train_memory = round(psutil.Process().memory_info().rss / (1024 ** 2), 2)
# 释放训练过程中的内存
del train_iter
net.zero_grad()
trainer.zero_grad()
d2l.evaluate_accuracy(net, test_iter)
test_memory = round(psutil.Process().memory_info().rss / (1024 ** 2), 2)
print(f'Memory for Train: {train_memory} MB')
print(f'Memory for Test: {test_memory} MB')Memory for Train: 483.33 MB
Memory for Test: 438.46 MB
4. 假设想计算二阶导数。计算图发生了什么?预计计算需要多长时间?
解:
想计算二阶导数,首先,必须保留反向传播的中间值,设置.backward(retain_graph=True);然后,使用自动求导torch.autograd.grad()计算二阶导数,需要设置create_graph=True,即在计算完梯度后保留计算图以便进行高阶导数计算。
计算二阶导数的时间开销更大,假设仍采用Fashion-MNIST数据集,和本节提到的模型,代码以及计算一阶和二阶导数花费的时间比较如下(大概是计算一阶导数所需时间的5倍):
import time
net = nn.Sequential(nn.Flatten(),
nn.Linear(784, 256),
nn.ReLU(),
nn.Linear(256, 10))
def init_weights(m):
if type(m) == nn.Linear:
nn.init.normal_(m.weight, std=0.01)
net.apply(init_weights)
batch_size, lr, wd = 256, 0.1, 0.5
# torch.autograd.grad()的输出必须是标量
# reduction='mean'确保输出是标量
loss = nn.CrossEntropyLoss(reduction='mean')
trainer = torch.optim.SGD([
{"params":net[1].weight,'weight_decay': wd},
{"params":net[1].bias},
{"params":net[3].weight,'weight_decay': wd},
{"params":net[3].bias}], lr=lr)
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)
def Caculate_derivative(params):
for X, y in train_iter:
# 计算梯度并更新参数
y_hat = net(X)
l = loss(y_hat, y)
break
# 保留计算图的中间值retain_graph=True
l.backward(retain_graph=True)
time1 = time.time()
grad1_w = torch.autograd.grad(l, params, create_graph=True)
time2 = time.time()
# 对一阶导数取平均,转为标量
out = grad1_w[0].mean()
out.backward(retain_graph=True)
grad2_w = torch.autograd.grad(out, params)
time3 = time.time()
return time2-time1, time3-time1
# 分别计算对w1和w2求一阶、二阶导数的时间
w1_1st, w1_2nd = Caculate_derivative(net[1].weight)
w2_1st, w2_2nd = Caculate_derivative(net[3].weight)
print("Calculation time for 1st derivative: {:.4f} seconds".format(w1_1st + w2_1st))
print("Calculation time for 2nd derivative: {:.4f} seconds".format(w1_2nd + w2_2nd))Calculation time for 1st derivative: 0.0016 seconds
Calculation time for 2nd derivative: 0.0077 seconds
5. 假设计算图对当前拥有的GPU来说太大了。
a. 请试着把它划分到多个GPU上。
解:
如果是数据过大,可用数据并行,将批处理数据分布到多个GPU上,每个GPU上都有一个完整的模型副本,并且在每个GPU上计算损失和梯度。然后,通过收集每个GPU上的梯度并进行同步,更新模型参数。这种方法适用于可以完整复制到每个GPU内存的模型。可以使用torch.nn.DataParallel模块实现数据并行。
如果是模型太大,无法完全放入单个GPU内存,可用模型并行,是指将模型的不同部分分布到多个GPU上,并在每个GPU上进行计算。需要手动分配不同部分的模型到不同的GPU上,并自定义前向传播和反向传播来实现模型并行。
b. 与小批量训练相比,有哪些优点和缺点?
解:
优点是多个GPU可以增加内存容量、加快训练速度并承载更大的批量;
缺点是在多个GPU之间传输数据和梯度需要额外的通信开销,这可能成为训练过程中的瓶颈,尤其是在GPU之间频繁交换大量数据时,当通信开销超过了并行计算所带来的性能提升时,效率反而下降,并且多GPU训练的模型参数同步需要额外的同步机制。