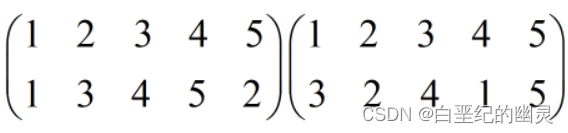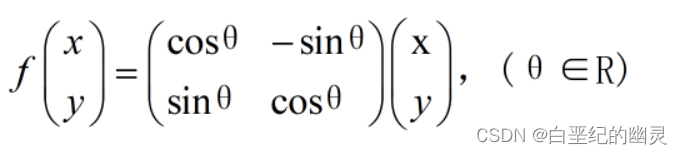例3:设S是一个集合A的所有变换作成的集合,定义r:a→a1=r(a),证明:我们可以用r1r2:a→r1[r2(a)]=r1r2(a)来规定一个S的乘法,这个乘法也适合结合律,并且对于这个乘法来说,ɛ(恒等变换)还是S的单位元。
证:①设任意的r1,r2∈S,任意的a∈A,则r1(a),r1[r2(a)]都是A中唯一确定的元,那么题中定义的r1r2是S中唯一确定的元,且是一个S的乘法;
②设任意的r3∈S,则有:
[(r1r2)r3](a) = r1r2[r3(a)] = r1{r2[r3(a)]},[r1(r2r3)](a) = r1[r2r3(a)] = r1{r2[r3(a)]},
所以(r1r2)r3 = r1(r2r3),即规定的乘法适合结合律;
③设r是S中的任意元,对于任意a∈A,都有ɛ(a) = a,因此有:
ɛr(a) = ɛ[r(a)] = r(a),rɛ(a) = r[ɛ(a)] = r(a),即ɛr = rɛ = r,所以ɛ还是S的单位元。
例4:证明:一个变换群的单位元是恒等变换。
证:设G为A上的一个变换群(A上的一一变换组成的集合),e是G的单位元,
因此对任意的f∈G,有e o f = f,
对任意的y∈A,因为f为A上的一一变换,所以存在x∈A,使得f(x) = y,
所以e(y) = e[f(x)] = (e o f)(x) = f(x) = y = ɛ(y),
即有e(y) = ɛ(y),即e = ɛ。
例5:定义在实数域上的n阶可逆矩阵的全体Mn关于矩阵的乘法作成群。【这个群称为n阶一般线性群,记为Gln(R)】
证:因为单位矩阵E可逆,因此Mn≠∅;
①设A,B∈Mn,则A,B可逆,且(AB)^(-1) = B^(-1)A^(-1),所以AB也可逆,即AB∈Mn,因此满足了群公理第一条的封闭性;
②矩阵的乘法适合结合律,因此也满足了群公理的第二条;
③对任意的A∈Mn,有EA = A,因此单位矩阵E即是Mn中的单位元,所以也满足了群公理的第四条;
④对任意的A∈Mn,因为A可逆,设其逆矩阵为A^(-1),则有AA^(-1) = E,因此A^(-1)也可逆,即A^(-1)∈Mn,所以对于Mn中任意的可逆矩阵A,A在Mn中都存在相应的逆矩阵(或者叫“逆元”),所以也满足了群公理的第五条。
综上所述,根据群的第二定义(或者说“第二判定定理”),我们可知Mn关于矩阵的乘法作成群。
置换群
定义1:有限集上的一一变换叫做“置换”,同一集合上的若干置换构成的群称为“置换群”。
【“置换群”和“变换群”的区别:“置换群”要求是“有限集”上的一一变换组成的群,而变换群则没有“有限集”这个限制条件,因此“置换群”是“变换群”的一种特殊形式。】
包含n个元素的集合上的全体置换作成的群称为“n次对称群”,记为Sn。
定理1(有限群的凯莱定理):任何一个有限群都同构于一个置换群。
通常,将Sn中的元素记为:
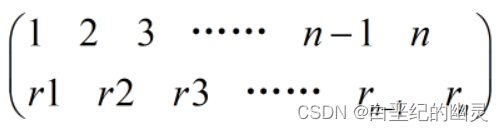
它表示某个置换σ,在这个置换下,1变成r1,2变成r2,……
比如:
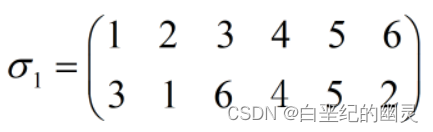
在置换σ1下,1变成3,3变成6,6变成2,2变成1,4,5保持不变,
这样的置换也可以简写成(1362)(前一个数字在置换下变成后一个数字,4,5保持不变所以可以省略),这样的置换可称为“4-循环”。
(r1r2......rk)称为一个“k-循环”(统称“循环置换”),其中“2-循环”也叫“对换”。
置换的计算:

解析:
①按从左往右乘,即先计算左边的矩阵,
左边的矩阵中1变成2,而在右边的矩阵中,2变回了1,因此两个矩阵相乘后的结果就是1变成1,即1保持不变;
左边的矩阵中2变成3,而在右边的矩阵中,3保持不变,因此两个矩阵相乘后的结果就是2变成3;
左边的矩阵中3变成1,而在右边的矩阵中,1变成了4,因此两个矩阵相乘后的结果就是3变成4;
左边的矩阵中4保持不变,而在右边的矩阵中,4变成了2,因此两个矩阵相乘后的结果就是4变成2;
综上,按从左往右乘的计算结果为:1保持不变,2变成3,3变成4,4变成2,可简写为(234)。
②按从右往左乘,即先计算右边的矩阵,
右边的矩阵中1变成4,而在左边的矩阵中,4保持不变,因此两个矩阵相乘后的结果就是1变成4;
右边的矩阵中2变成1,而在左边的矩阵中,1变回了2,因此两个矩阵相乘后的结果就是2保持不变;
右边的矩阵中3保持不变,而在左边的矩阵中,3变成了1,因此两个矩阵相乘后的结果就是3变成1;
右边的矩阵中4变成了2,而在左边的矩阵中,2变成了3,因此两个矩阵相乘后的结果就是4变成3;
综上,按从右往左乘的计算结果为:2保持不变,1变成4,4变成3,3变成1,可简写为(143)。
(待续……)