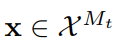题目地址
求解平方根,但是返回的是整数,则用二分法,如果是真的求解一个平方根的近似值,可以采用零点定理和牛顿迭代法,那种是可以求出小数值的。
1. 思路
求某数 a ( a ≥ 0 ) a(a\ge 0) a(a≥0)的平方根,可以用二分查找的思想来查找,这种二分的思想,时间复杂度是 O ( l o g ( n ) ) O(log(n)) O(log(n)),首先在 a ≥ 0 a\ge 0 a≥0时, 0 ≤ a ≤ a 0 \le \sqrt{a} \le a 0≤a≤a,因此,我们确定其解的搜索范围一定是在 [ 0 , a ] [0,a] [0,a]中,我们可以让二分查找的left赋值为0,right赋值为a,然后进行二分查找,因为我们取的就是估计值,所以我们没法设定 middle = a \text{middle}=\sqrt{a} middle=a(即 middle 2 = a \text{middle}^{2}=a middle2=a)的情况下返回middle,我们只能去二分地逼近它,因此,我们最后的思路是:在区间 [ 0 , a ] [0,a] [0,a]使用二分查找,查找满足 middle = a \text{middle}=\sqrt{a} middle=a(即 middle 2 = a \text{middle}^{2}=a middle2=a)条件的值,由于最后结果是整数,所以我们求得的结果不一定是满足middle * middle == a这样的情况,所以我们不能像二分查找那样找到满足middle * middle == a条件后return middle,参考之前LeetCode34在排序数组中查找元素的第一个和最后一个位置的想法,是否我们可以让迭代一直进行下去,直到找到左边界(即小于等于这个平方根取整的结果)或者右边界(即大于等于这个平方根取整的结果),但是这个题列举的连续区间都是严格递增的整数,不会出现重复序列,因此让迭代进行下去也不会出现找到重复的整数的情况,下面举个例子,假设我们求的是 a , a = 3 \sqrt{a},a=3 a,a=3,那就相当于在整数序列[0, 1, 2, 3]中找到根号3的整数部分。
1.1 两种基本情况
还是和之前的题目一样,求解的时候分清楚解的情况:
情况1:开平方根结果正好是个整数,如 4 = 2 \sqrt{4}=2 4=2
情况2:开平方根结果是个小数,需要取整,如 3 ≈ 1.732050807569 \sqrt{3}\approx 1.732050807569 3≈1.732050807569
1.2 按找右边界的思路实现
按照LeetCode34的思路,我们需要魔改一下二分查找的循环条件,以下是魔改后的结果:
class Solution {
public:
// 左闭右闭
int mySqrt(int a) {
int left = 0;
int right = a;
//当left大于right就跳出循环停止迭代
while(left <= right)
{
int middle = left + ((right - left) >> 1);//右移1位相当于除2,节省时间
if(a >= (long long)middle * (long long)middle)
{
left = middle + 1;
}
else
{
right = middle - 1;
}
}
return right;//写成left-1也行,下文会解释
}
};
1.2.1 开平方根结果是个小数,需要取整
以求解 a , a = 3 \sqrt{a},a=3 a,a=3为例:
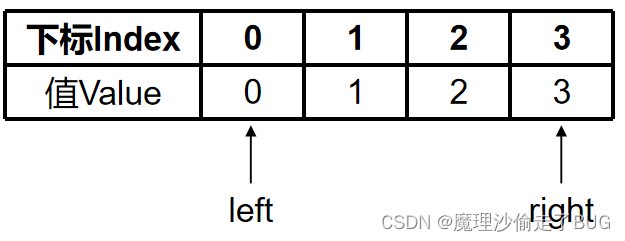
第1步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 3 − 0 2 ⌋ + 0 = 1 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{3-0}{2}\right\rfloor+0=1 middle =⌊2 right − left ⌋+ left =⌊23−0⌋+0=1

a = 3 > ( nums [ middle ] ) 2 = ( nums [ 1 ] ) 2 = 1 2 = 1 \text{a}=3>(\text{nums}[\text{middle}])^{2}=(\text{nums}[1])^{2}=1^{2}=1 a=3>(nums[middle])2=(nums[1])2=12=1,故 left = middle + 1 = 1 + 1 = 2 < right = 3 \text{left}=\text{middle}+1=1+1=2<\text{right}=3 left=middle+1=1+1=2<right=3,满足循环条件,继续循环

第2步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 3 − 2 2 ⌋ + 2 = 2 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{3-2}{2}\right\rfloor+2=2 middle =⌊2 right − left ⌋+ left =⌊23−2⌋+2=2

a = 3 < ( nums [ middle ] ) 2 = ( nums [ 2 ] ) 2 = 2 2 = 4 \text{a}=3<(\text{nums}[\text{middle}])^{2}=(\text{nums}[2])^{2}=2^{2}=4 a=3<(nums[middle])2=(nums[2])2=22=4,故 right = middle − 1 = 2 − 1 = 1 < left = 2 \text{right}=\text{middle}-1=2-1=1<\text{left}=2 right=middle−1=2−1=1<left=2,不满足循环条件,跳出循环

我们知道,在数学上, 3 ≈ 1.732050807569 \sqrt{3}\approx 1.732050807569 3≈1.732050807569,而我们要找的是它的整数部分1,righ(或者left-1)恰好符合(middle-1也可以,这种情况下我们需要在循环外设置一个变量来保存middle-1的结果),于是就有了上面的代码,但是我们还要观察一下第二种情况
1.2.2 开平方根结果正好是个整数
以求解 a , a = 4 \sqrt{a},a=4 a,a=4为例:

第1步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 4 − 0 2 ⌋ + 0 = 2 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{4-0}{2}\right\rfloor+0=2 middle =⌊2 right − left ⌋+ left =⌊24−0⌋+0=2
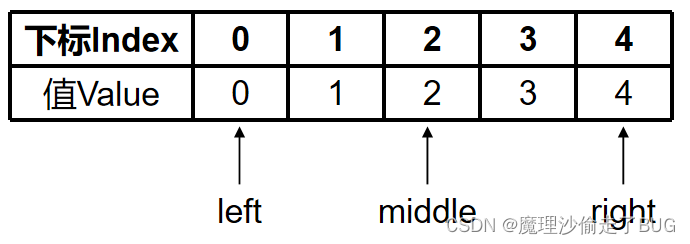
a = 4 = ( nums [ middle ] ) 2 = ( nums [ 2 ] ) 2 = 2 2 = 4 \text{a}=4=(\text{nums}[\text{middle}])^{2}=(\text{nums}[2])^{2}=2^{2}=4 a=4=(nums[middle])2=(nums[2])2=22=4,故 left = middle + 1 = 2 + 1 = 3 < right = 4 \text{left}=\text{middle}+1=2+1=3<\text{right}=4 left=middle+1=2+1=3<right=4,满足循环条件,继续循环

第2步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 4 − 3 2 ⌋ + 3 = 3 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{4-3}{2}\right\rfloor+3=3 middle =⌊2 right − left ⌋+ left =⌊24−3⌋+3=3
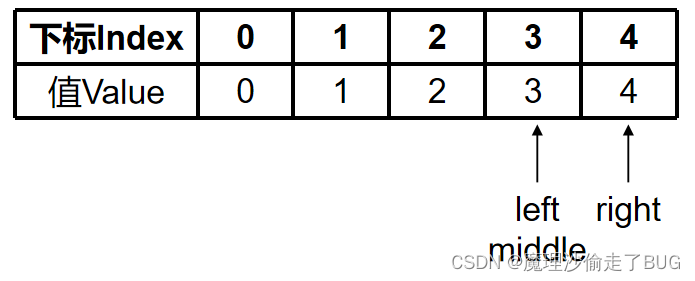
a = 4 < ( nums [ middle ] ) 2 = ( nums [ 3 ] ) 2 = 3 2 = 9 \text{a}=4<(\text{nums}[\text{middle}])^{2}=(\text{nums}[3])^{2}=3^{2}=9 a=4<(nums[middle])2=(nums[3])2=32=9,故 right = middle − 1 = 3 − 1 = 2 < left = 3 \text{right}=\text{middle}-1=3-1=2<\text{left}=3 right=middle−1=3−1=2<left=3,不满足循环条件,跳出循环
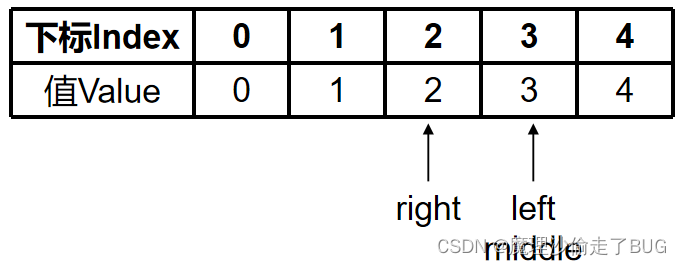
我们可以看到,返回right或者left-1确实是要找的目标值,算法是成立的。
1.2.3 代码实现
代码实现就如我们之前推理的一样,这里再放一遍:
class Solution {
public:
// 左闭右闭
int mySqrt(int a) {
int left = 0;
int right = a;
//当left大于right就跳出循环停止迭代
while(left <= right)
{
int middle = left + ((right - left) >> 1);//右移1位相当于除2,节省时间
if(a >= (long long)middle * (long long)middle)
{
left = middle + 1;
}
else
{
right = middle - 1;
}
}
return right;//写成left-1也行,下文会解释
}
};
1.3 按找左边界的思路实现
我们试试效仿LeetCode34中找左边界的思路,找左边界的思路就是把循环中的if条件改一下(逻辑上取反一下):
while(left <= right)
{
int middle = left + ((right - left) >> 1);//右移1位相当于除2,节省时间
if(a <= (long long)middle * (long long)middle)
{
right = middle - 1;
}
else
{
left = middle + 1;
}
}
1.3.1 开平方根结果是个小数,需要取整
以求解 a , a = 3 \sqrt{a},a=3 a,a=3为例:

第1步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 3 − 0 2 ⌋ + 0 = 1 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{3-0}{2}\right\rfloor+0=1 middle =⌊2 right − left ⌋+ left =⌊23−0⌋+0=1

a = 3 > ( nums [ middle ] ) 2 = ( nums [ 1 ] ) 2 = 1 2 = 1 \text{a}=3>(\text{nums}[\text{middle}])^{2}=(\text{nums}[1])^{2}=1^{2}=1 a=3>(nums[middle])2=(nums[1])2=12=1,故 left = middle + 1 = 1 + 1 = 2 < right = 3 \text{left}=\text{middle}+1=1+1=2<\text{right}=3 left=middle+1=1+1=2<right=3,满足循环条件,继续循环

第2步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 3 − 2 2 ⌋ + 2 = 2 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{3-2}{2}\right\rfloor+2=2 middle =⌊2 right − left ⌋+ left =⌊23−2⌋+2=2

a = 3 < ( nums [ middle ] ) 2 = ( nums [ 2 ] ) 2 = 2 2 = 4 \text{a}=3<(\text{nums}[\text{middle}])^{2}=(\text{nums}[2])^{2}=2^{2}=4 a=3<(nums[middle])2=(nums[2])2=22=4,故 right = middle − 1 = 2 − 1 = 1 < left = 2 \text{right}=\text{middle}-1=2-1=1<\text{left}=2 right=middle−1=2−1=1<left=2,不满足循环条件,跳出循环

这个过程和1.2.1的过程是一样的,看似我们的返回结果也应该是right
1.3.2 开平方根结果正好是个整数
以求解 a , a = 4 \sqrt{a},a=4 a,a=4为例:

第1步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 4 − 0 2 ⌋ + 0 = 2 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{4-0}{2}\right\rfloor+0=2 middle =⌊2 right − left ⌋+ left =⌊24−0⌋+0=2

a = 4 = ( nums [ middle ] ) 2 = ( nums [ 2 ] ) 2 = 2 2 = 4 \text{a}=4=(\text{nums}[\text{middle}])^{2}=(\text{nums}[2])^{2}=2^{2}=4 a=4=(nums[middle])2=(nums[2])2=22=4,故 right = middle − 1 = 4 − 1 = 3 > left = 0 \text{right}=\text{middle}-1=4-1=3>\text{left}=0 right=middle−1=4−1=3>left=0,满足循环条件,继续循环

第2步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 3 − 0 2 ⌋ + 0 = 1 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{3-0}{2}\right\rfloor+0=1 middle =⌊2 right − left ⌋+ left =⌊23−0⌋+0=1
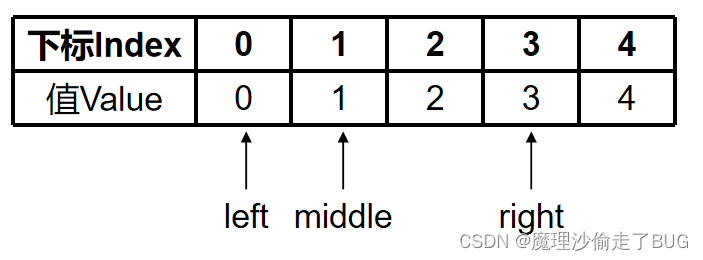
a = 4 > ( nums [ middle ] ) 2 = ( nums [ 1 ] ) 2 = 1 2 = 1 \text{a}=4>(\text{nums}[\text{middle}])^{2}=(\text{nums}[1])^{2}=1^{2}=1 a=4>(nums[middle])2=(nums[1])2=12=1,故 left = middle + 1 = 1 + 1 = 2 < right = 3 \text{left}=\text{middle}+1=1+1=2<\text{right}=3 left=middle+1=1+1=2<right=3,满足循环条件,继续循环

第3步:
middle = ⌊ right − left 2 ⌋ + left = ⌊ 3 − 2 2 ⌋ + 2 = 2 \text { middle }=\left\lfloor\frac{\text { right }- \text { left }}{2}\right\rfloor+\text { left }=\left\lfloor\frac{3-2}{2}\right\rfloor+2=2 middle =⌊2 right − left ⌋+ left =⌊23−2⌋+2=2

a = 4 = ( nums [ middle ] ) 2 = ( nums [ 2 ] ) 2 = 2 2 = 4 \text{a}=4=(\text{nums}[\text{middle}])^{2}=(\text{nums}[2])^{2}=2^{2}=4 a=4=(nums[middle])2=(nums[2])2=22=4,故 right = middle − 1 = 2 − 1 = 1 < left = 2 \text{right}=\text{middle}-1=2-1=1<\text{left}=2 right=middle−1=2−1=1<left=2,不满足循环条件,跳出循环

这里就不是返回right或者left-1了,应该返回的是left,和1.3.1的情况冲突了,我们发现,恰好是两种不同的情况导致的。
1.3.3 两种情况整合和代码实现
为了能够兼容两种情况,我们在结尾设置一个循环,如果(right+1)的平方恰好是a(也就是开平方根结果正好是个整数),则返回right+1,否则不变,这样就将两种情况区分开来:
class Solution {
public:
// 左闭右闭
int mySqrt(int a) {
int left = 0;
int right = a;
//当left大于right就跳出循环停止迭代
while(left <= right)
{
int middle = left + ((right - left) >> 1);//右移1位相当于除2,节省时间
if(a <= (long long)middle * (long long)middle)
{
right = middle - 1;
}
else
{
left = middle + 1;
}
}
if(long(right+1) * long(right+1) == a)
{
return right + 1;
}
else
{
return right;
}
}
};