课程13 光在晶体中的传播(一)（视频P47-49）

光在晶体中的传播

晶体双折射

晶体简介：外形有一定规则性或对称性，内部原子排列有序、周期性，规则有序结构导致物理性质各向异性----------热传导的各向异性、电导的、极化的、磁化的、光速的各向异性等。

光在晶体中的传播------光在各向异性介质中的传播的行为------《固体物理》、《晶体几何理论》
表明： 7种晶系、14种晶格、32种点群。
其中 按照光学眼光划分，可分为 单轴晶系（冰洲石、红宝石、石英）、双轴晶系（蓝宝石、云母）、立方晶系（食盐Nacl 晶粒）

双折射现象

光在单轴晶系中传播时表现出来一种双折射现象。一束光正入射晶体表面，出现两束出射光，出射光中有一束光正常射出(O光)，另一束光有一个位移，在晶体内倾斜出射（e光）。我们采用偏振片检验，O光e光都是线偏振光。

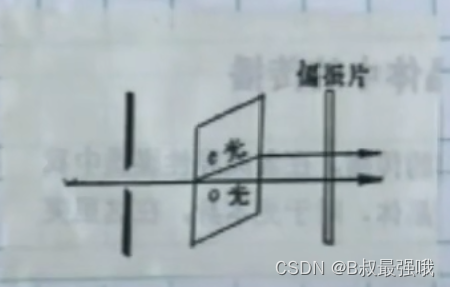
方解石，其自然解理面为平行六面体。平行六面体中8个顶角，只有两个顶角是钝角，这两个角组成的传播方向是晶体的光轴方向，经过光轴方向传播的光束不会发生双折射。

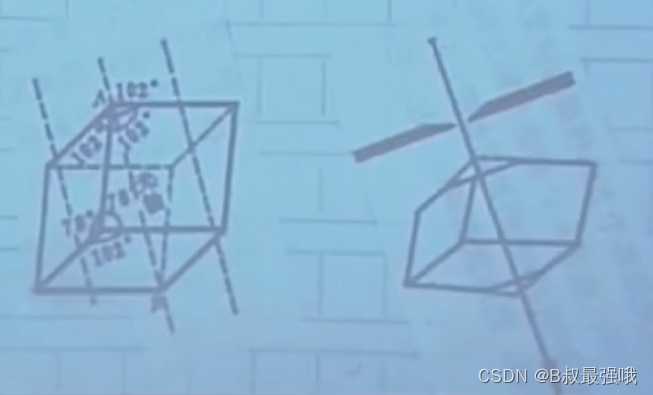
光轴：单轴晶体存在一个特殊方向----光轴，光沿光轴方向传播不会发生双折射。冰川石光轴方向------平行于两个钝棱角的对角线方向。

晶体中的惠更斯作图法----------求 e光 O光的传播方向

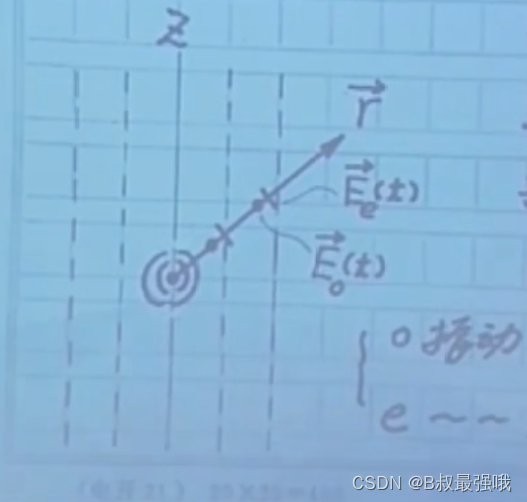
设想当前光轴是Z轴。晶体内一点源，沿任意方向产生考察波传播行为，应分别为 O振动、e振动而论。O振动，光矢量E0(t)垂直于珠光面(Z,r)。e振动，光矢量Ee(t)平行于主平面(Z,r)。

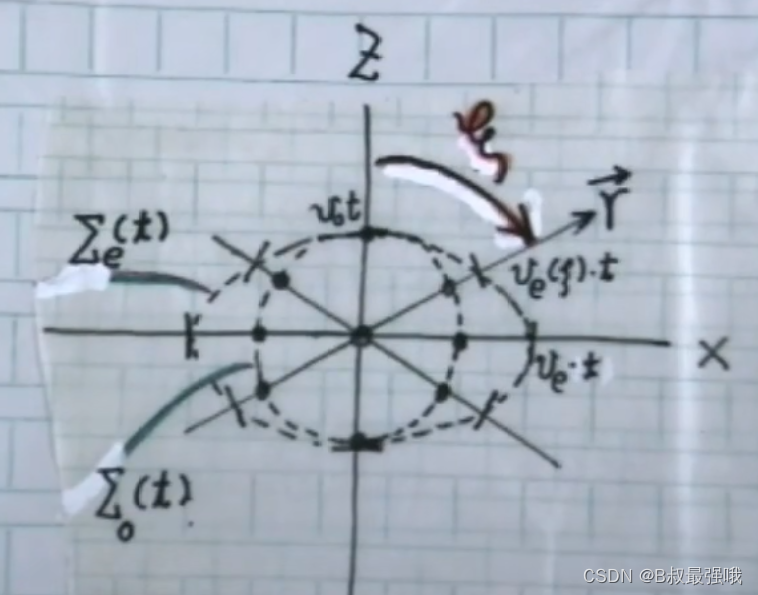
在t时刻看O光的波面是一个球面，而e光的波面则是一个旋转的椭圆面。旋转轴是光轴，长轴Ve t ，短轴Vo t。以光轴为参考周，斜的方向标定，则有φ角，射线方向φ角变化。
冰洲石(负晶体) Ve(φ)>= Vo,或者 ne(φ)<= no。
石英(正晶体，各向同性)，Ve(φ)<= Vo,或者 ne(φ)>= no。
可归纳为：
(1) O振动传播规律--------各向同性，O光波面∑o(t) 为球面
(2) e振动传播规律---------各向异性，e光波面∑e(t) 为旋转椭球面，旋转轴为光轴；两套波面相切于光轴方向。

对于负晶体 no >= ne(φ)>= ne
对于正晶体 no <= ne(φ)<= ne
其实，主折射率有3个(nx，ny，nz)
对于单轴而言 nx=ny=ne，nz = no。
对于 Ve(φ)各向异性的又一认识----------取决于光矢量E(t) 与光轴Z之间的夹角。

深化认识 晶体光学的各向异性 表现认识：no →ne(φ) → ne 或 Vo → Ve(φ) → Ve
只要知道主折射率，就可以通过作图的办法求出晶体中O光e光的传播方向。

注意：e光波面的法线方向不是e的射线方向
入射面：入射光线与界面的法线方向所组成的面
主截面：界面的法线方向与晶体内部光轴所组成的面
主平面：传播方向与光轴组成的面。
当主截面与入射面相重合的时候，主平面也与入射面相重合。
对于e光而言还可能出现(不满足折射定律)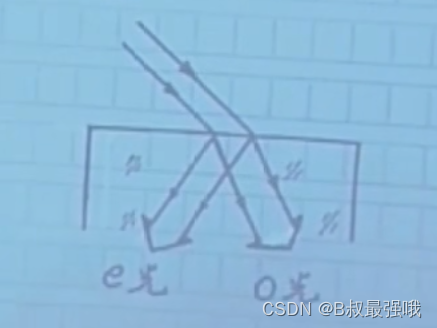
总之，(1)O光满足通常的折射定律，e光的折射方向不满足施耐德定律的形式；
(2) O光线与其波面∑o正交，而e光 re 与其波面不正交。或者说，一般情况下，e光波的射线方向与其波面法线方向并不一致。

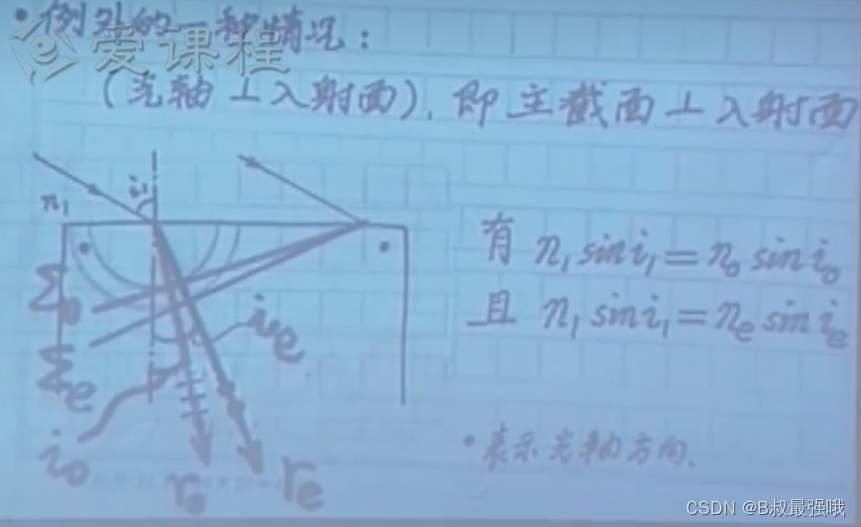
例外的一种情况：光轴垂直于入射面，即主截面垂直于入射面

两个重要情况---------均为厚度均匀晶片
(1) 光轴平行表面、光束正入射，
可见 o光e光出射方向一致，表观上无双折射现象，却内涵双折射。两者于晶体内部传播，光程不等(no d - ne d)≠0，这将被应用产生或检查 圆偏振光、椭圆偏振光。(波晶片)

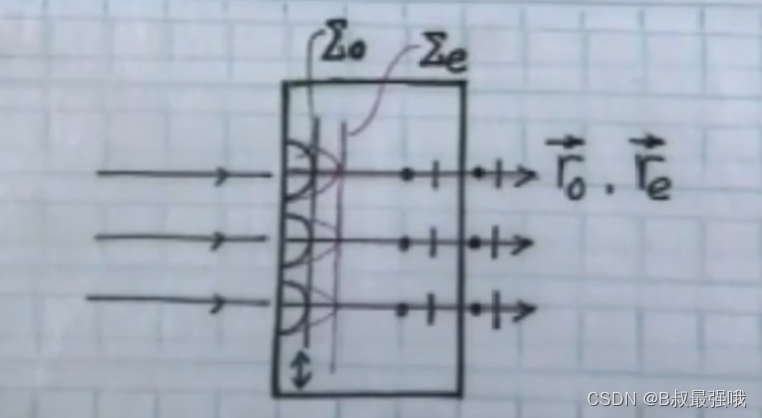
(2) 光轴任意、光束正入射

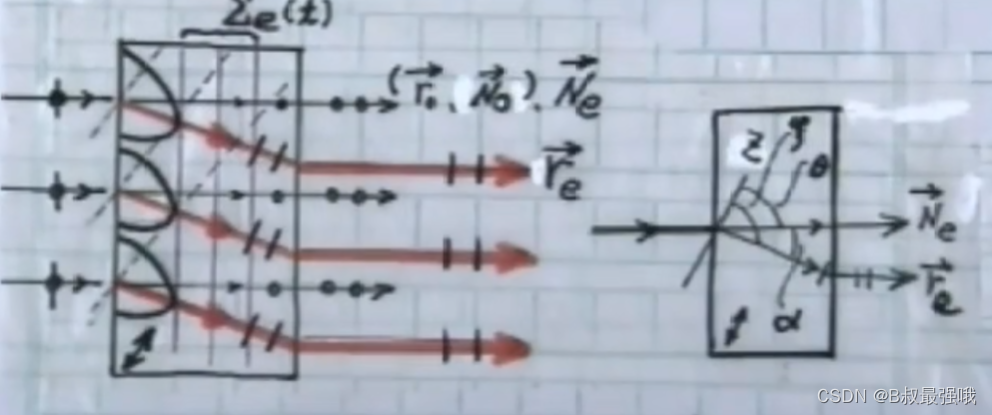
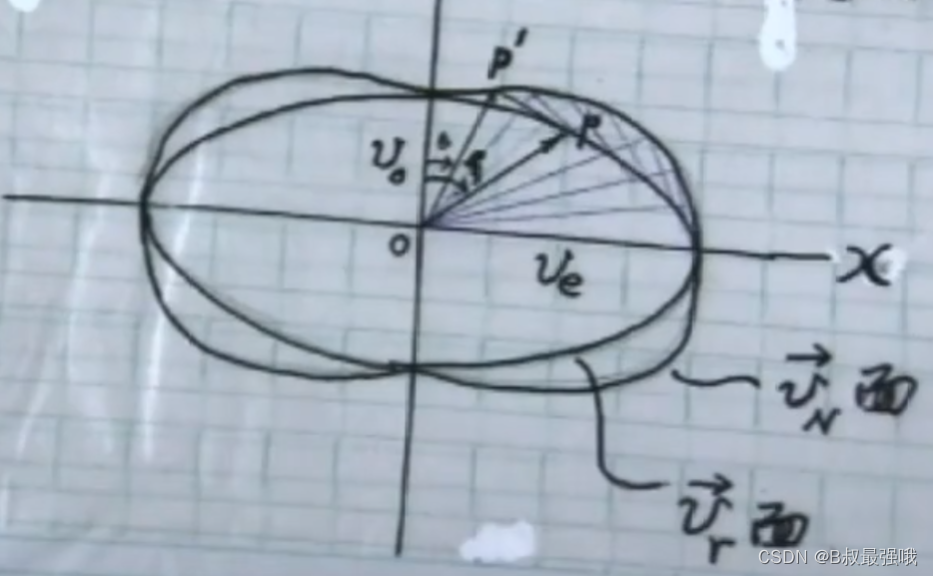
可见，体内∑e 面法线方向Ne 与射线方向re 不一致，二者分离角 α；而∑e 面依然平行晶片表面。
在晶体内部e光的波面随时间在空间中推移，e光波面法线方向与能流射线方向并不一定正交。波面的法线方向与光轴的夹角为θ，射线方向与光轴的夹角为 ξ ，α = ξ - θ。

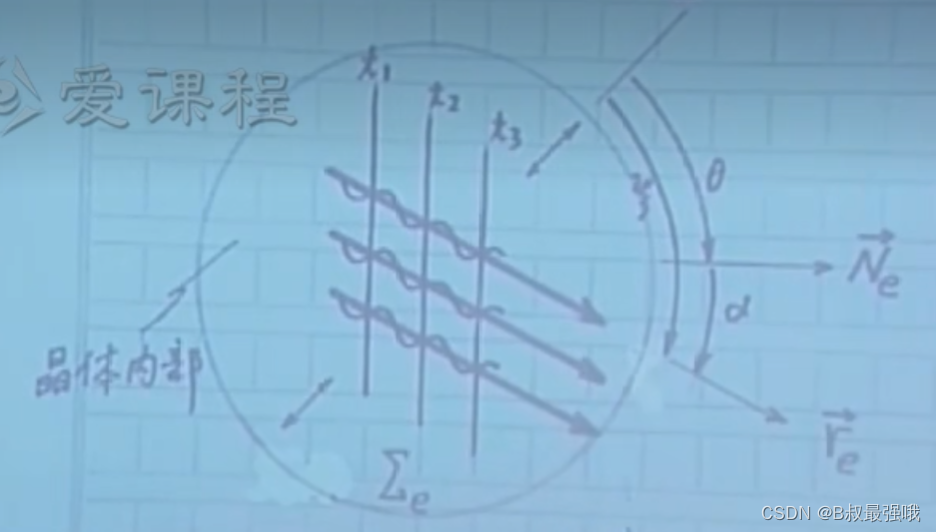
单轴晶体光学公式 双轴晶体

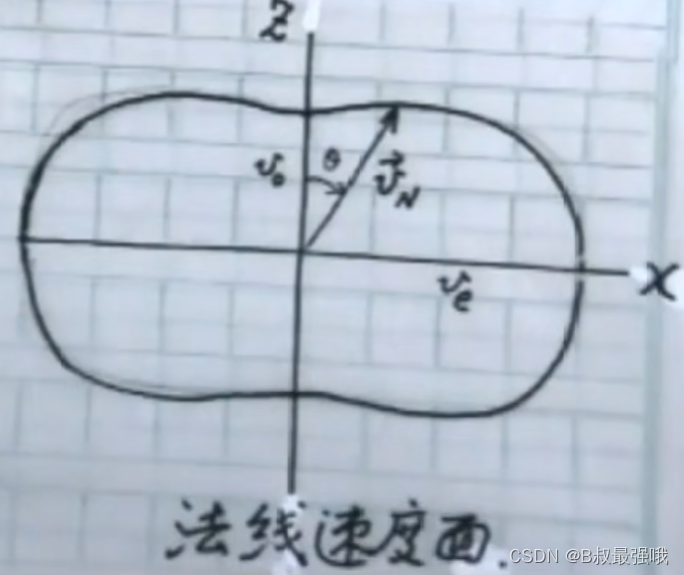
射线速度与法线速度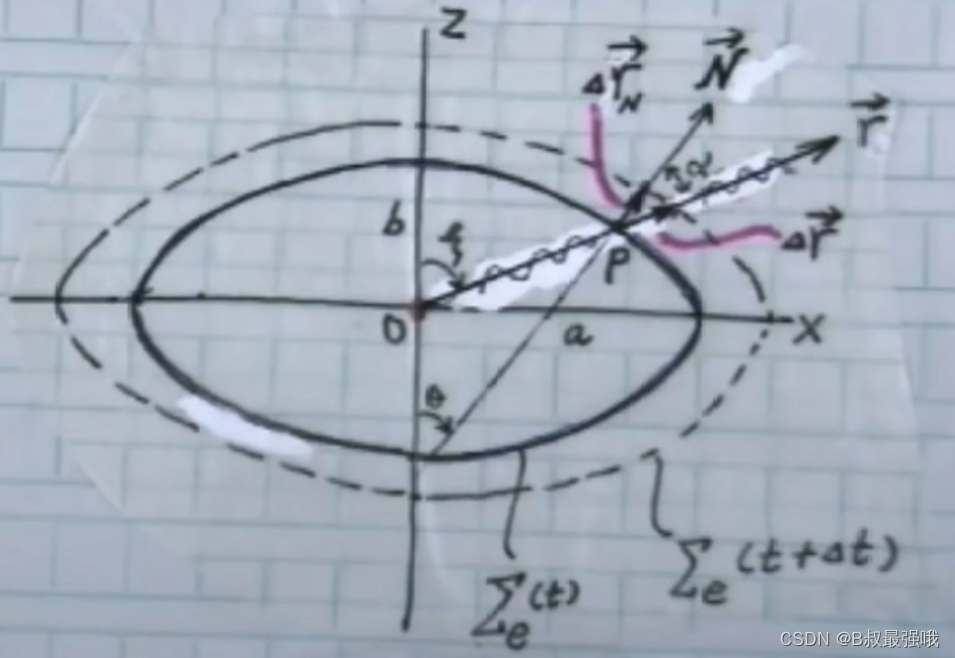

由于e光是一个椭球面，将3维信息退化为2维，在xz平面内讨论问题。t时刻，波面是一个椭圆，t+△t ，波面是一个大的椭球面，e光随着时间波面在空间中推移。
均匀介质各向异性，扰动是直线传播的。扰动的方向就是直线传播的方向就是射线的方向。另一个方向是一个面的法线方向。可提取速度的概念。
考虑波面∑e(t) ----------随时间在空间的推移，出发点-----------惠更斯模型
∑e(t) 为旋转椭球面，其主轴速度为 (Vx,Vy,Vz) = (Ve,Ve,Vo)。即(x,z)面内，椭圆方程有
$$\frac{x^2}{a^2}+\frac{z^2}{b^2}=1,其中a=V_{e}t，b=V_{o}t$$
提取速度的概念∑e(t) → ∑e(t+△t) ,则有
(1) 射线速度 Vr = dr/dt ，具有物理意义
(2) 法线方向 Vn=drn /dt，具有几何意义

VrV 与Vn 的关系
对场点P而言
$$V_n(P)=V_r(P)cos\alpha ,\alpha =\xi -\theta ,tan\theta =\frac{n_e^2}{n_o^2}tan\xi$$
可见(1) Vn <= Vr
(2) ξ 从0° → π/2时，θ 也从0°→ π/2，α 从0°→0°
其间出现极大值α ----------最大分离角
当tanθ0 = ne/no时，出现最大分离角 αM，满足
$$tan{\alpha }_M=\frac{n_o^2-n_e^2}{2n_o{n}_e}$$

导出θ → ξ 关系
$$\frac{x^2}{a^2}+\frac{z^2}{b^2}=1$$
同时求导可得
$$\frac{1}{a^2}2xdx+\frac{1}{b^2}2zdz=0$$
于是，切线斜率
$$\frac{dz}{dx}=-\frac{b^2}{a^2}\frac{x}{z}=-\frac{n_e^2}{n_o^2}tan\xi ,其中a=V_{e}t=\frac{c}{n_e}，b=V_{o}t=\frac{c}{n_o}$$
其法线斜率，若以θ角来表示，当为
$$tan\theta =-\frac{dz}{dx}=\frac{n_e^2}{n_o^2}tan\xi$$
波面的法线方向与光轴方向无关，一定是表面的法线方向，就是e光的波面法线方向。我们若已知α角，则射线方向就可以确定下来。

速度各向异性公式

Vr(ξ)公式
由 r² = x² + z² ，以改写波面椭圆方程
极坐标形式
$$r(\xi {)}^2=\frac{a^2{b}^2}{a^2(cos\xi {)}^2+b^2(sin\xi {)}^2}=\frac{V_o^2{V}_e^2}{V_e^2(cos\xi {)}^2+V_o^2(sin\xi {)}^2}{t}^2$$
于是，射线速度各向异性公式可写为
$$V_r(\xi {)}^2=\frac{r(\xi {)}^2}{t^2}=\frac{V_o^2{V}_e^2}{V_e^2(cos\xi {)}^2+V_o^2(sin\xi {)}^2}$$
Vn(θ)公式可根据
$$V_n(\theta {)}^2=V_r(\xi {)}^2(cos(\xi -\theta ){)}^2，tan\theta =\frac{n_e^2}{n_o^2}tan\xi$$
导出
$$V_n(\theta {)}^2=V_o^2(cos\theta {)}^2+V_e^2(sin\theta {)}^2$$

速度面及其倒数面-----------折射率面

人们为了形象的反映速度各向异性的公式，在三维空间中画出速度面--------2个自由度用在标定方向上，1个自由度用在反映速度数值上。
Vr(ξ)公式是一个标准极坐标的椭圆方程，Vn(θ)公式不是一个椭圆方程，是一个卵型。


不能单纯的认为 Vn(θ)>Vr(ξ)，因为 θ与ξ是成对出现的，是不独立的。
Vn(θ)公式会随着no/ne的不同而曲线形状存在差异。

射线折射率 nr = c/ Vr； 法线折射率 n = C/Vn。
速度面的倒数面，即是 折射率面。
(1) 由 Vr(ξ)² 公式得
$$n_r(\xi {)}^2=n_o^2(cos\xi {)}^2+n_e^2(sin\xi {)}^2$$
这里no = c/Vo，ne = c/Ve，它倒变成了卵型。

(2) 由 Vn(θ)² 公式得
$$n(\theta {)}^2=\frac{n_o^2{n}_e^2}{n_e^2(cos\theta {)}^2+n_o^2(sin\theta {)}^2}$$
它倒符合椭圆了。

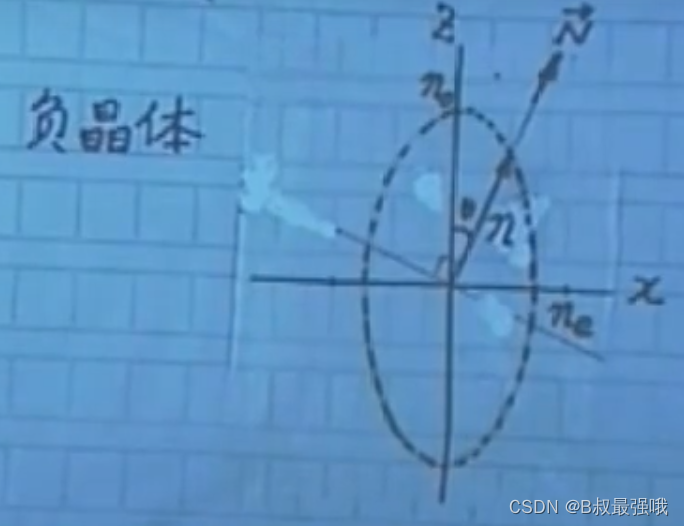
在三维空间中，法线折射率面便是一个旋转椭球面。不过通常转90°画出。

来自晶体光学 电磁理论的补充内容

某些结论
(1) 各向异性介质中 D不平行 E，晶体主轴方向(XYZ)
$$D_x={ϵ}_x{E}_x,D_y={ϵ}_y{E}_y,D_z={ϵ}_z{E}_z$$
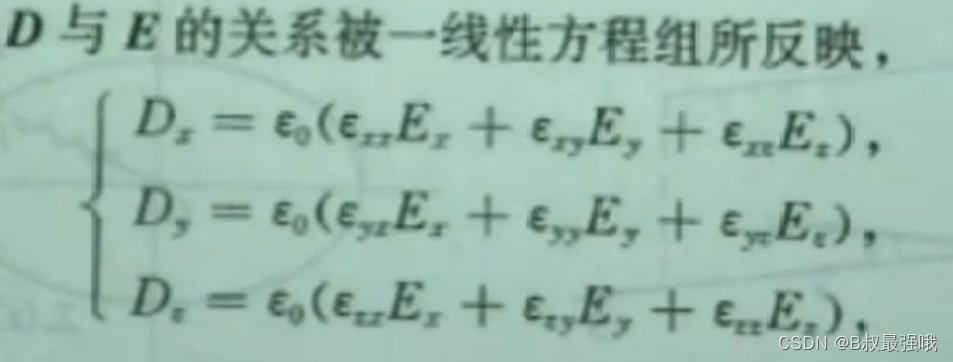3x3的矩阵元构成了介质的介电张量，它反映了各向异性介质的电学三个正交的特殊方向(xyz)，使得介电张量“对角化”，即

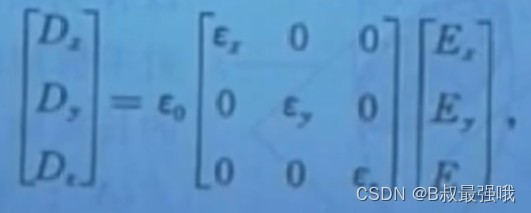
对角化后，在晶体的主轴方向，比如，对于单轴晶体，
$$D_x={ϵ}_0{ϵ}_x{E}_x,D_y={ϵ}_0{ϵ}_y{E}_y,D_z={ϵ}_0{ϵ}_z{E}_z$$
对应三个主轴的光学折射率即主折射率为
$$n_x=\sqrt{{ϵ}_x},n_y=\sqrt{{ϵ}_y},n_z=\sqrt{{ϵ}_z}$$
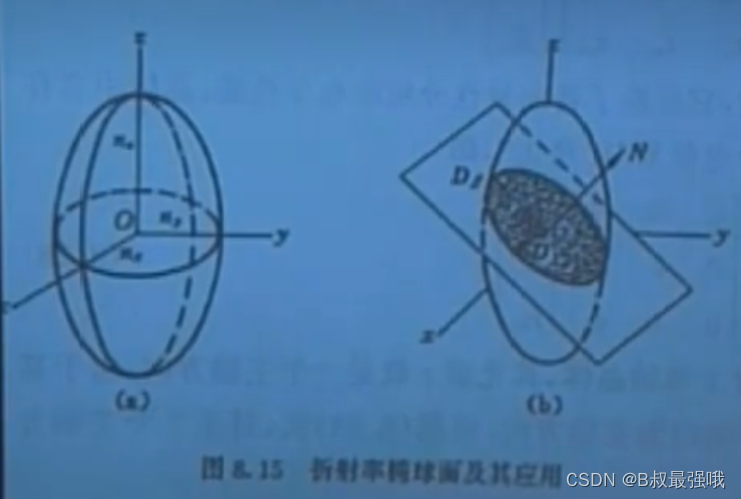
波法线与射线方向一致，晶体光学各向异性的法向折射率可以用椭球面方程的形式表示
$$\frac{x^2}{n_x^2}+\frac{y^2}{n_y^2}+\frac{z^2}{n_z^2}=1$$
对于单轴晶体，nx=ny=no，nz=ne；
对于双轴晶体，nx≠ny≠nz；
立方晶体或非晶介质nx=ny=nz=n

(2) (D,E,H)与(r,N)之关系。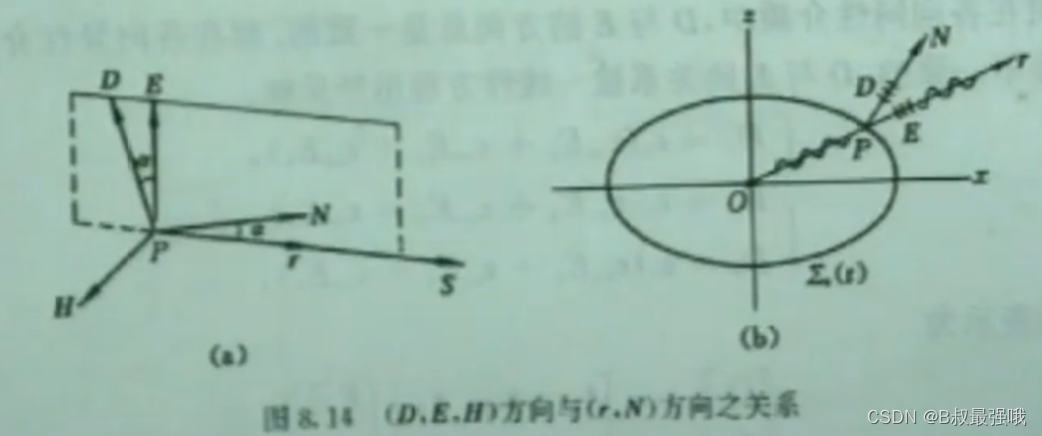
E x H // r，D x H // N

和N正交的方向就是D的方向，那段的长度就是法向的折射率。
双轴晶体，其情况比较复杂，从折射率椭球而言，三轴折射率彼此不一样，也是一个折射率椭球。这样一个椭球，在三个正交平面里轨迹都是椭圆，但是在一个特定的方向，平面与其相交，其交面是一个圆。在这个特定横平面方向就无所谓长短轴了，法向速度就一个了，这个方向就是光轴方向，根据对称性，这个方向有两个。

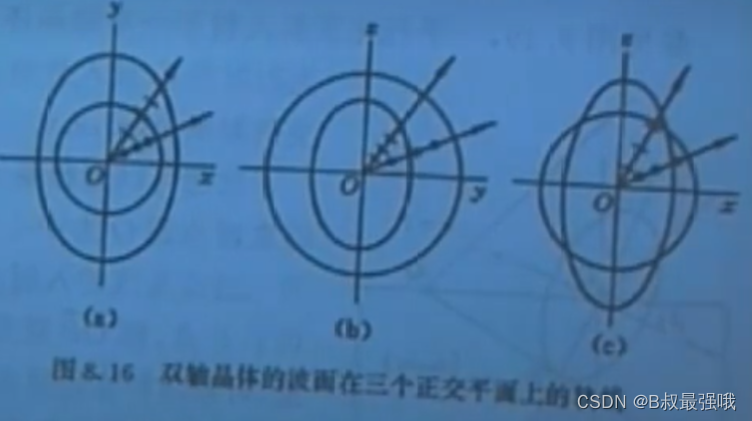
具体说，双轴晶体波面比较复杂。在xy平面里看的光的传播某一个时刻的波面，总是有一个圆一个卵型线。在yz平面里，也是一个圆一个卵型线，与相联系的振动。在xz平面里，球面的波面与卵型面的波面会套连起来，相交与一个点。以上三图，是nx<ny<nz绘制出来的结果。

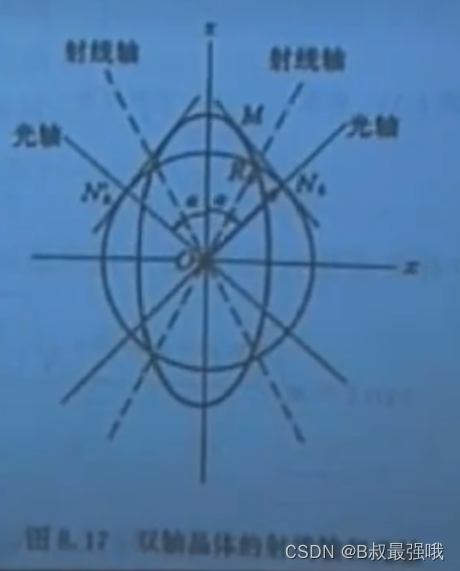
XZ平面上，圆轨迹与卵型轨迹相交于R0点，做一条切线切于卵型面和圆形面，则从圆点到圆形面切线交点为光轴方向，OR0为射线轴方向。根据对称性，右侧也有一个光轴和射线轴。
单轴晶体，光轴就是Z轴。光轴存在两个含义：在光轴方向O振动E振动已经失去意义，O的传播速度与E的传播速度一样；在光轴上，E光的射线速度与法线速度一样。

R0点----------酒窝点

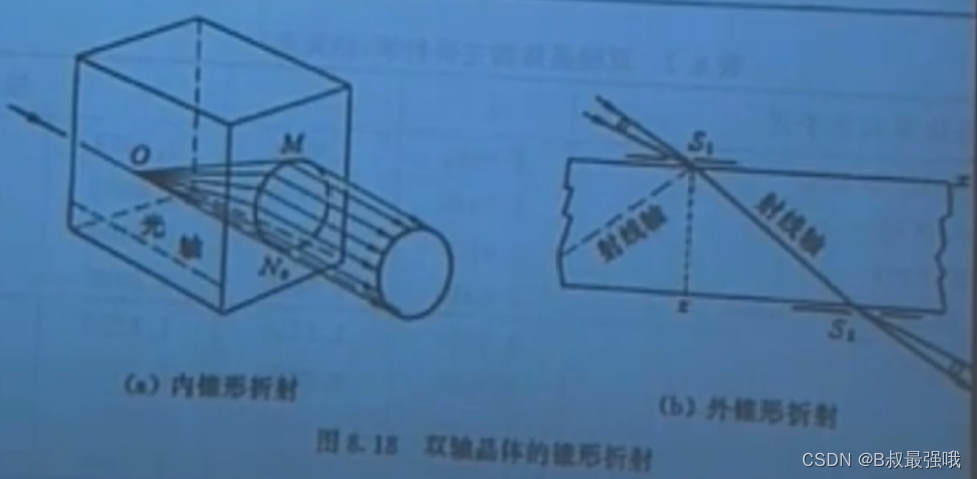
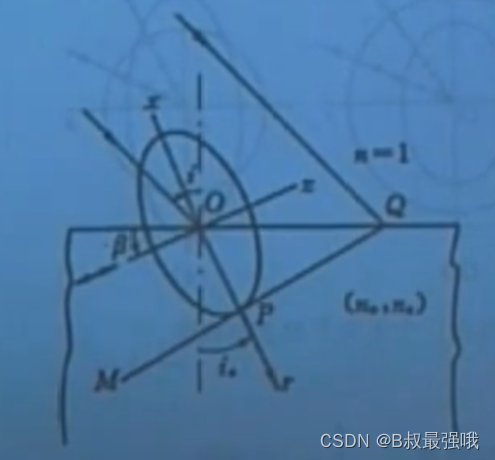
求斜入射斜光轴时e光折射角----------主截面与入射面一致，定量来确认光折射方向。利用椭圆外一点切椭圆，根据解析几何的知识，求出切点P的坐标即可求出光折射角i1。

参考内容

1、http://www.icourses.cn/sCourse/course_3571.html