1.概述
1.1.单载波传输
均衡输出: y ( t ) = ∑ m = − ∞ ∞ a m g ( t − m T ) + z ( t ) y\left(t\right)=\sum_{m=-\infty}^{\infty}a_{m}g\left(t-mT\right)+z\left(t\right) y(t)=∑m=−∞∞amg(t−mT)+z(t);
系统总体的脉冲响应: g ( t ) = g T x ( t ) ∗ h ( t ) ∗ g R x ( t ) ∗ h − 1 ( t ) g\left(t\right)=g_{Tx}\left(t\right)*h\left(t\right)*g_{Rx}\left(t\right)*h^{-1}\left(t\right) g(t)=gTx(t)∗h(t)∗gRx(t)∗h−1(t);
忽略噪声影响,均衡采样的输出: y ( t n ) = ∑ m = − ∞ ∞ a m g ( ( n − m ) T ) , t n = n T y\left(t_{n}\right)=\sum_{m=-\infty}^{\infty}a_{m}g\left(\left(n-m\right)T\right),t_{n}=nT y(tn)=∑m=−∞∞amg((n−m)T),tn=nT, n n n是第 n n n个码元,T是码元周期;
第 n n n个采样值: y ( t n ) = a n g ( 0 ) + ∑ m = − ∞ , m ≠ n ∞ a m g ( ( n − m ) T ) y\left(t_{n}\right)=a_{n}g\left(0\right)+\sum_{m=-\infty,m\neq n}^{\infty}a_{m}g\left(\left(n-m\right)T\right) y(tn)=ang(0)+∑m=−∞,m=n∞amg((n−m)T), ∑ m = − ∞ , m ≠ n ∞ a m g ( ( n − m ) T ) \sum_{m=-\infty,m\neq n}^{\infty}a_{m}g\left(\left(n-m\right)T\right) ∑m=−∞,m=n∞amg((n−m)T)是拖尾项对 a n g ( 0 ) a_{n}g\left(0\right) ang(0)产生的ISI;
为了尽量降低或彻底消除ISI,必须仔细设计接收滤波器和发射滤波器。使得总的传输特性奈奎斯特准则如下, g ( n T ) = δ [ n ] = { 1 , n = 0 0 , n ≠ 0 g\left(nT\right)=\delta\left[n\right]=\begin{cases}1,&n=0\\0,&n\neq0\end{cases} g(nT)=δ[n]={1,0,n=0n=0,或者 ∑ i = − ∞ ∞ G ( f − i T ) = T \sum_{i=-\infty}^{\infty}G\left(f-\frac iT\right)=T ∑i=−∞∞G(f−Ti)=T;

为了支持每秒传输 R s R_s Rs个符号的速率,所需的最小传输带宽为奈奎斯特带宽,即为 R s / 2 R_s/2 Rs/2,在单载波情况下,为追求更大的传输速率,需要更大的传输带宽。信号带宽随着符号速率的增大而增大。当信号带宽大于无线信道的相干带宽时,链路会受到多径衰落的影响,从而会产生IS1。由于接收机的均衡器过于复杂,高数据速率的单载波传输是不可行的。
1.2.多载波传输
为了克服单载波传输下的频率选择性衰弱,使用多载波,具体是对信道的频率划分为多个子区间(子区间频率几乎不变,平坦,同时子区间不相交)。在此基础上,OFDM允许子区间有重叠(正交,实际中通过DFT和IDFT实现),并且所有的自区间共用滤波。将传输信号通过IDFT分成不同的频率成分 x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] ⋅ e i 2 π k n N x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{i 2\pi \frac{kn}{N}} x[n]=N1∑k=0N−1X[k]⋅ei2πNkn
F ( ω ) = ∫ − ∞ ∞ f ( t ) ⋅ e − i ω t d t F(\omega) = \int_{-\infty}^{\infty} f(t) \cdot e^{-i\omega t} dt F(ω)=∫−∞∞f(t)⋅e−iωtdt
f ( t ) = 1 2 π ∫ − ∞ ∞ F ( ω ) ⋅ e i ω t d ω f(t) = \frac{1}{2\pi} \int_{-\infty}^{\infty} F(\omega) \cdot e^{i\omega t} d\omega f(t)=2π1∫−∞∞F(ω)⋅eiωtdω
X [ k ] = ∑ n = 0 N − 1 x [ n ] ⋅ e − i 2 π k n N X[k] = \sum_{n=0}^{N-1} x[n] \cdot e^{-i 2\pi \frac{kn}{N}} X[k]=∑n=0N−1x[n]⋅e−i2πNkn
x [ n ] = 1 N ∑ k = 0 N − 1 X [ k ] ⋅ e i 2 π k n N x[n] = \frac{1}{N} \sum_{k=0}^{N-1} X[k] \cdot e^{i 2\pi \frac{kn}{N}} x[n]=N1∑k=0N−1X[k]⋅ei2πNkn
1.3.OFDM 基本原理
时间有限的复指数信号 { e j 2 π / f k t } k = 0 N − 1 \left\{e^{j2\pi/f_kt}\right\}_{k=0}^{N-1} {ej2π/fkt}k=0N−1, f k = k / T s y m f_{k}=k/T_{sym} fk=k/Tsym, 0 ≤ 1 ≤ T s y m 0\leq1\leq T_{sym} 0≤1≤Tsym
1.3.1.正交 & 调制解调
正交
1 T s y m ∫ 0 T s y m e j 2 π f k t e − j 2 π f i t d t = 1 T s y m ∫ 0 T n y m e j 2 π k T s y m t e − j 2 π i T s y m t d t = 1 T s y m ∫ 0 T s y m e j 2 π ( k − i ) T s y m t d t = { 1 , ∀ k = i 0 , 其他 \begin{aligned} \frac{1}{T_{\mathrm{sym}}}\int_{0}^{T_{\mathrm{sym}}}e^{j2\pi f_{k}t}e^{-j2\pi f_{i}t}dt& =\frac{1}{T_{sym}}\int_{0}^{T_{nym}}e^{j2\pi\frac{k}{T_{sym}}t}e^{-j2\pi\frac{i}{T_{sym}}t}dt \\ &=\frac{1}{T_{sym}}\int_{0}^{T_{sym}}e^{j2\pi\frac{\left(k-i\right)}{T_{sym}}t}dt \\ &\left.=\left\{\begin{matrix}1,&\forall k=i\\0,&\text{其他}\end{matrix}\right.\right. \end{aligned} Tsym1∫0Tsymej2πfkte−j2πfitdt=Tsym1∫0Tnymej2πTsymkte−j2πTsymitdt=Tsym1∫0Tsymej2πTsym(k−i)tdt={1,0,∀k=i其他
t = n T s = n T s y m / N , n = 0 , 1 , 2 , ⋯ , N − 1 t=nT_{s}=nT_{sym}/N,n=0,1,2,\cdots,N-1 t=nTs=nTsym/N,n=0,1,2,⋯,N−1
1 N ∑ n = 0 N − 1 e j 2 π k T s m . n T s e − j 2 π i T . n T s = 1 N ∑ n = 0 N − 1 e j 2 π k T s y m ⋅ n T N e − j 2 π i T s y m ⋅ n T s y m N = 1 N ∑ n = 0 N − 1 e j 2 π ( k − i ) N n = { 1 , ∀ k = i 0 , 其他 \begin{aligned} \frac{1}{N}\sum_{n=0}^{N-1}e^{j2\pi\frac{k}{T_{sm}}.nT_{s}}e^{-j2\pi\frac{i}{T}.nT_{s}}& =\frac{1}{N}\sum_{n=0}^{N-1}e^{j2\pi\frac{k}{T_{sym}}\cdot\frac{nT}{N}}e^{-j2\pi\frac{i}{T_{sym}}\cdot\frac{nT_{sym}}{N}} \\ &=\frac{1}{N}\sum_{n=0}^{N-1}e^{j2\pi\frac{\left(k-i\right)}{N}n} \\ &=\begin{cases}1,&\forall k=i\\0,&\text{其他}\end{cases} \end{aligned} N1n=0∑N−1ej2πTsmk.nTse−j2πTi.nTs=N1n=0∑N−1ej2πTsymk⋅NnTe−j2πTsymi⋅NnTsym=N1n=0∑N−1ej2πN(k−i)n={1,0,∀k=i其他
调制解调
先将信息比特映射成一个PSK或QAM符号序列,之后将符号序列转换成 N N N个并行符号流(串并转换),被不同的子载波调制。
➡️第 k k k个子载波上第 l l l个发送的符号, X l [ k ] X_{l}\left[k\right] Xl[k], l = 0 , 1 , 2 , ⋯ , ∞ , k = 0 , 1 , 2 , ⋯ , N − 1 l=0,1,2,\cdots,\infty,k=0,1,2,\cdots,N-1 l=0,1,2,⋯,∞,k=0,1,2,⋯,N−1;
➡️ T s y m = N T s T_{sym}=NT_{s} Tsym=NTs;
➡️第 k k k个子载波上第 l l l个发送的OFDM符号, Ψ l , k ( t ) = { e j 2 π g k ( t − l T s y m ) , 0 < t ⩽ T s y m 0 , 其他 \Psi_{l,k}\left(t\right)=\begin{cases}\mathrm{e}^{\mathrm{j}2\pi g_{k}\left(t-lT_{sym}\right)},&0<t\leqslant T_{sym}\\0,&\text{其他}\end{cases} Ψl,k(t)={ej2πgk(t−lTsym),0,0<t⩽Tsym其他;
➡️通频带, x l ( t ) = R e { 1 T s y m ∑ l = 0 ∞ { ∑ k = 0 N − 1 X l [ k ] Ψ l , k ( t ) } } x_{l}\left(t\right)=\mathrm{Re}\left\{\frac{1}{T_{sym}}\sum_{l=0}^{\infty}\left\{\sum_{k=0}^{N-1}X_{l}\left[k\right]\Psi_{l,k}\left(t\right)\right\}\right\} xl(t)=Re{Tsym1∑l=0∞{∑k=0N−1Xl[k]Ψl,k(t)}}
➡️基带信号, x l ( t ) = ∑ l = 0 ∞ ∑ k = 0 N − 1 X l [ k ] e j 2 π f k ( t − l T s y m ) x_{l}\left(t\right)=\sum_{l=0}^{\infty}\sum_{k=0}^{N-1}X_{l}\left[k\right]e^{j2\pi f_{k}\left(t-lT_{sym}\right)} xl(t)=∑l=0∞∑k=0N−1Xl[k]ej2πfk(t−lTsym)
➡️ t = l T s y m + n T s , T s = T s y m / N , f k = k / T s y m t=lT_{sym}+nT_{s},T_{s}=T_{sym}/N,f_{k}=k/T_{sym} t=lTsym+nTs,Ts=Tsym/N,fk=k/Tsym采样
x l [ n ] = ∑ k = 0 N − 1 X l [ k ] e j 2 π k n / N , n = 0 , 1 , ⋯ , N − 1 x_{l}\left[n\right]=\sum_{k=0}^{N-1}X_{l}\left[k\right]e^{j2\pi kn/N},\quad n=0,1,\cdots,N-1 xl[n]=k=0∑N−1Xl[k]ej2πkn/N,n=0,1,⋯,N−1
这个形式是 PSK 或 QAM 数据符号 { X l [ k ] } k = 0 N − 1 \left\{X_{l}\left[k\right]\right\}_{k=0}^{N-1} {Xl[k]}k=0N−1的 N 点 IDFT
➡️基带 OFDM 接收符号, y l ( t ) = ∑ k = 0 N − 1 X l [ k ] e j 2 π f k ( t − l T s y m ) , l T s y m < t < l T s y m + n T s y_{l}\left(t\right)=\sum_{k=0}^{N-1}X_{l}\left[k\right]\mathrm{e}^{j2\pi f_{k}\left(t-lT_{\mathrm{sym}}\right)},lT_{\mathrm{sym}}<t<lT_{\mathrm{sym}}+nT_{\mathrm{s}} yl(t)=∑k=0N−1Xl[k]ej2πfk(t−lTsym),lTsym<t<lTsym+nTs
➡️重构原发送符号
Y 1 [ k ] = 1 T s y m ∫ − ∞ ∞ y l ( t ) e − j 2 π k f k ( t − l T s y m ) d t = 1 T s y m ∫ ∞ ∞ ∑ i = 0 N − 1 { X l [ i ] e j 2 π f l ( t − l T s y m ) } e − j 2 π f k ( t − l T s y m ) d t = ∑ i = 0 N − 1 X l [ i ] { 1 T s y m ∫ 0 T s y m e j 2 π ( f i − f k ) ( t − l T s y m ) d t } = X l [ k ] \begin{aligned} Y_{1}\left[k\right]& =\frac{1}{T_{sym}}\int_{-\infty}^{\infty}y_{l}\left(t\right)e^{-j2\pi kf_{k}\left(t-lT_{sym}\right)}dt \\ &=\frac{1}{T_{sym}}\int_{\infty}^{\infty}\sum_{i=0}^{N-1}\left\{X_{l}\left[i\right]e^{j2\pi f_{l}\left(t-lT_{sym}\right)}\right\}e^{-j2\pi f_{k}\left(t-lT_{sym}\right)}dt \\ &=\sum_{i=0}^{N-1}X_{l}\left[i\right]\left\{\frac{1}{T_{sym}}\int_{0}^{T_{sym}}e^{j2\pi\left(f_{i}-f_{k}\right)\left(t-lT_{sym}\right)}dt\right\}=X_{l}\left[k\right] \end{aligned} Y1[k]=Tsym1∫−∞∞yl(t)e−j2πkfk(t−lTsym)dt=Tsym1∫∞∞i=0∑N−1{Xl[i]ej2πfl(t−lTsym)}e−j2πfk(t−lTsym)dt=i=0∑N−1Xl[i]{Tsym1∫0Tsymej2π(fi−fk)(t−lTsym)dt}=Xl[k]
➡️令 { y 1 [ n ] } n = 0 N − 1 \left\{y_{1}\left[n\right]\right\}_{n=0}^{N-1} {y1[n]}n=0N−1为 OFDM接收符号 y l y_{l} yl在 t = l T s y c n + n T s t=lT_{\mathrm{sycn}}+nT_{s} t=lTsycn+nTs时刻的采样,则可得上式的离散形式,
Y 1 [ k ] = ∑ n = 0 N − 1 y i [ n ] e j 2 π k n / N = ∑ n = 0 N − 1 { 1 N ∑ i = 0 N − 1 X i [ i ] e j 2 π i n / N } e − j 2 π k n / N = 1 N ∑ n = 0 N − 1 ∑ i = 0 N − 1 X i [ i ] e j 2 π ( i − k ) n / N = X 1 [ k ] \begin{aligned} Y_{1}\left[k\right]& =\sum_{n=0}^{N-1}y_{i}\left[n\right]e^{j2\pi kn/N} \\ &=\sum_{n=0}^{N-1}\left\{\frac{1}{N}\sum_{i=0}^{N-1}X_{i}\left[i\right]e^{j2\pi in/N}\right\}e^{-j2\pi kn/N} \\ &=\frac{1}{N}\sum_{n=0}^{N-1}\sum_{i=0}^{N-1}X_{i}\left[i\right]e^{j2\pi\left(i-k\right)n/N}=X_{1}\left[k\right] \end{aligned} Y1[k]=n=0∑N−1yi[n]ej2πkn/N=n=0∑N−1{N1i=0∑N−1Xi[i]ej2πin/N}e−j2πkn/N=N1n=0∑N−1i=0∑N−1Xi[i]ej2π(i−k)n/N=X1[k]
这不就是 { y 1 [ n ] } n = 0 N − 1 \left\{y_{1}\left[n\right]\right\}_{n=0}^{N-1} {y1[n]}n=0N−1的N 点 DFT吗?

1.3.2.OFDM 保护间隔
多径信道会对OFDM符号造成ISI影响,破坏了子载波间的正交性。
➡️ x l ( t ) = ∑ k = 0 N − 1 X l [ k ] e j 2 π f k ( t − v T s y m ) , l T s y m < t ⩽ l T s y m + n T s x_{l}\left(t\right)=\sum_{k=0}^{N-1}X_{l}\left[k\right]\mathrm{e}^{\mathrm{j}2\pi f_{k}\left(t-vT_{sym}\right)},\quad lT_{\mathrm{sym}}<t\leqslant lT_{\mathrm{sym}}+nT_{s} xl(t)=∑k=0N−1Xl[k]ej2πfk(t−vTsym),lTsym<t⩽lTsym+nTs
➡️ y 1 ( t ) = x 1 ( t ) ∗ h 1 ( t ) + z 1 ( t ) = ∫ 0 ∞ h 1 ( τ ) x i ( t − τ ) d t + z i ( t ) , l T s y m < t ⩽ l T s y m + n T s y_{1}\left(t\right)=x_{1}\left(t\right)^{*}h_{1}\left(t\right)+z_{1}\left(t\right)=\int_{0}^{\infty}h_{1}\left(\tau\right)x_{i}\left(t-\tau\right)\mathrm{d}t+z_{i}\left(t\right),\quad lT_{\mathrm{sym}}<t\leqslant lT_{\mathrm{sym}}+nT_{s} y1(t)=x1(t)∗h1(t)+z1(t)=∫0∞h1(τ)xi(t−τ)dt+zi(t),lTsym<t⩽lTsym+nTs
➡️在 n T s = n T s y m / N nT_{s}=nT_{sym}/N nTs=nTsym/N采样
y 1 [ n ] = x 1 [ n ] ∗ h 1 [ n ] + z 1 [ n ] = ∑ m = 0 ∞ h 1 [ m ] x 1 [ n − m ] + z 1 [ n ] y_{1}\left[n\right]=x_{1}\left[n\right]*h_{1}\left[n\right]+z_{1}\left[n\right]=\sum_{m=0}^{\infty}h_{1}\left[m\right]x_{1}\left[n-m\right]+z_{1}\left[n\right] y1[n]=x1[n]∗h1[n]+z1[n]=∑m=0∞h1[m]x1[n−m]+z1[n],
x 1 [ n ] = x 1 ( n T s ) , y 1 [ n ] = y 1 ( n T s ) , h l [ n ] = h l ( n T s ) , z l [ n ] = z l ( n T s ) x_{1}\left[n\right]=x_{1}\left(nT_{s}\right),\quad y_{1}\left[n\right]=y_{1}\left(nT_{s}\right),\quad h_{l}\left[n\right]=h_{l}\left(nT_{s}\right),\quad z_{l}\left[n\right]=z_{l}\left(nT_{s}\right) x1[n]=x1(nTs),y1[n]=y1(nTs),hl[n]=hl(nTs),zl[n]=zl(nTs)
➡️
➡️
➡️

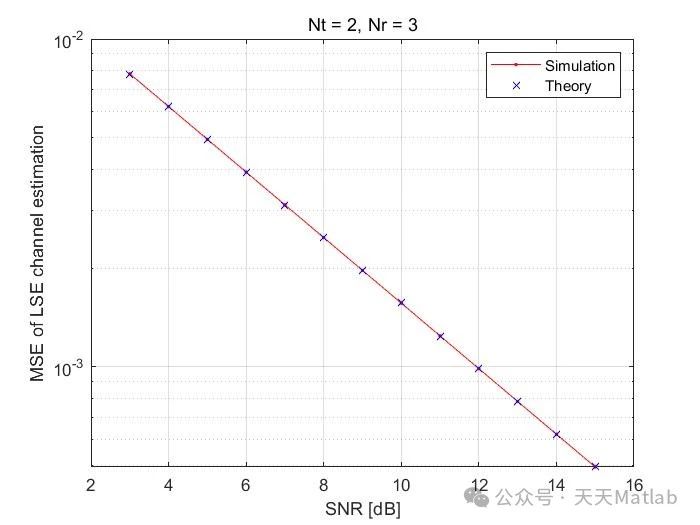
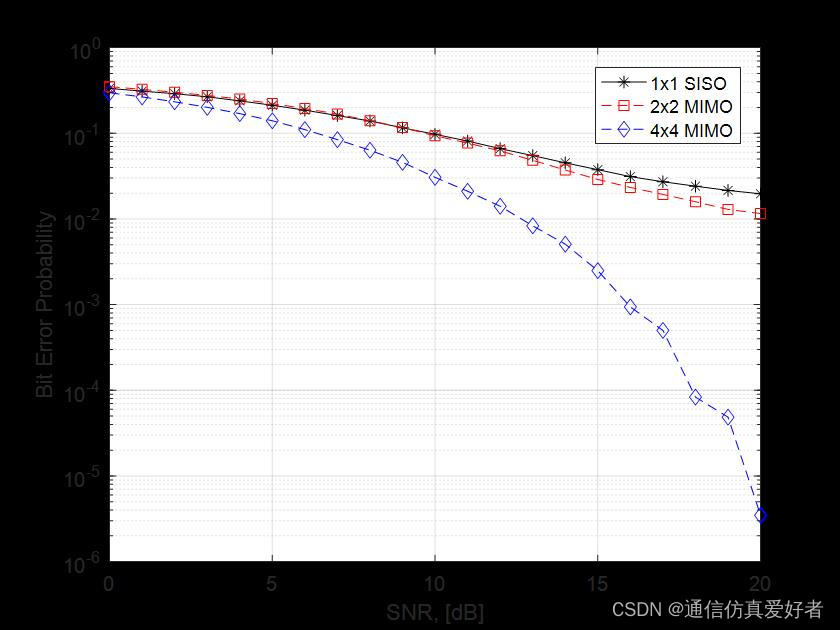
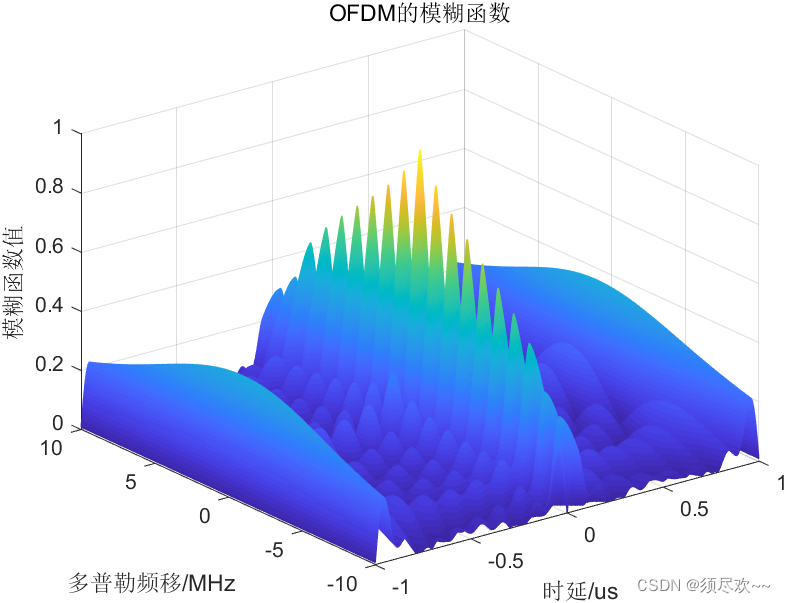
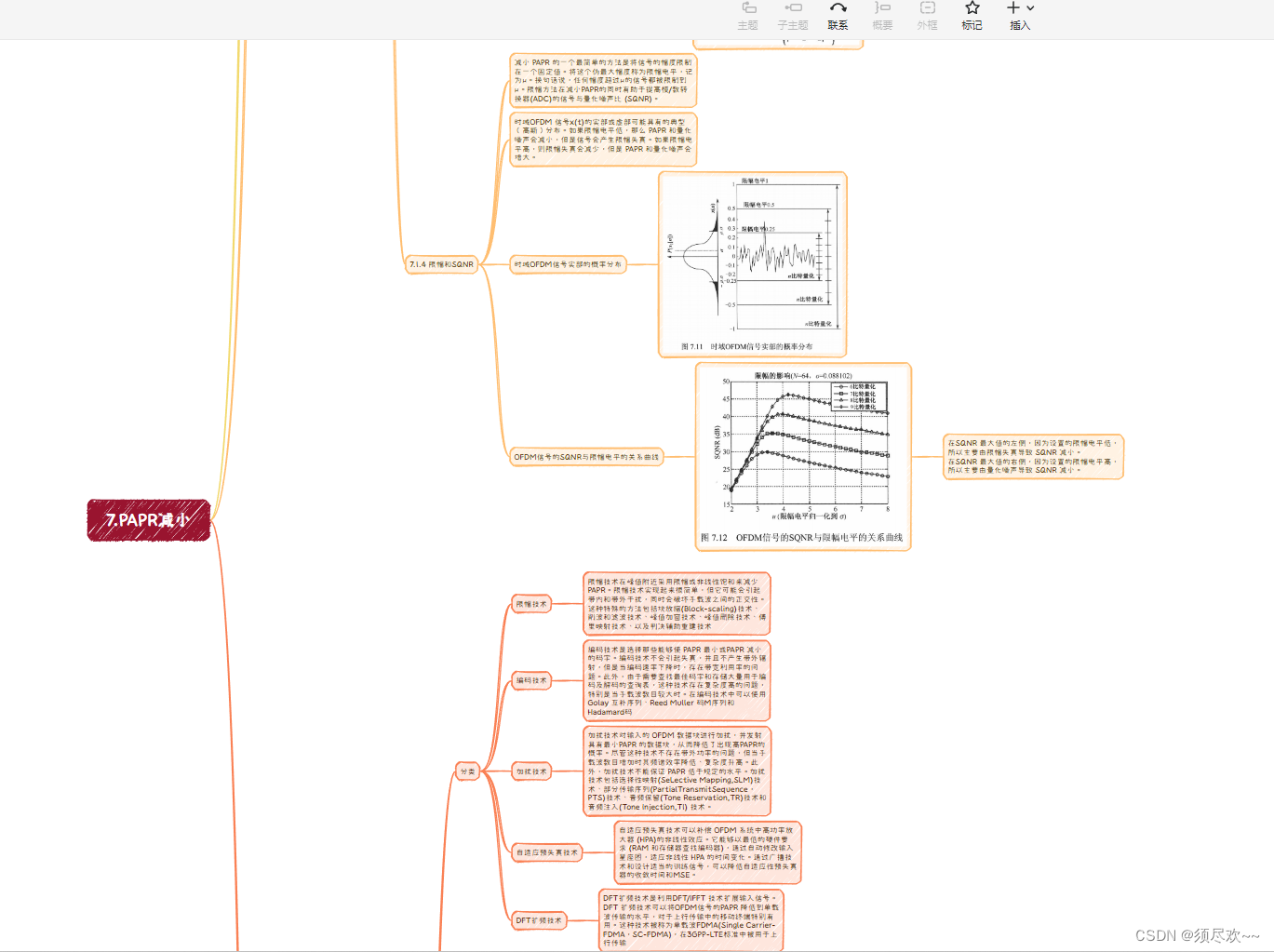

















![每日一题 --- 链表相交[力扣][Go]](https://img-blog.csdnimg.cn/img_convert/19233eb562fc6560bf2b50e0db71f441.png)