Codeforces Round 934 (Div. 1 ABCD1 题) 讲解

A. MEX Game 1

Problem Statement

Alice and Bob play yet another game on an array $a$ of size $n$ . Alice starts with an empty array $c$ . Both players take turns playing, with Alice starting first.

On Alice’s turn, she picks one element from $a$ , appends that element to $c$ , and then deletes it from $a$ .

On Bob’s turn, he picks one element from $a$ , and then deletes it from $a$ .

The game ends when the array $a$ is empty. Game’s score is defined to be the MEX $^\dagger$ of $c$ . Alice wants to maximize the score while Bob wants to minimize it. Find game’s final score if both players play optimally.

$^\dagger$ The $\operatorname{MEX}$ (minimum excludant) of an array of integers is defined as the smallest non-negative integer which does not occur in the array. For example:

The MEX of $[2, 2, 1]$ is $0$ , because $0$ does not belong to the array.
The MEX of $[3, 1, 0, 1]$ is $2$ , because $0$ and $1$ belong to the array, but $2$ does not.
The MEX of $[0, 3, 1, 2]$ is $4$ , because $0$ , $1$ , $2$ and $3$ belong to the array, but $4$ does not.

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ( $\leq t \leq 2 \cdot 10^4$ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $\le n \le 2 \cdot 10^5$ ).

The second line of each test case contains $n$ integers $a_1, a_2, \ldots, a_n$ ( $\le a_i < n$ ).

It is guaranteed that the sum of $n$ over all test cases does not exceed $\cdot 10^5$ .

Output

For each test case, find game’s score if both players play optimally.

Example

input
3
4
0 0 1 1
4
0 1 2 3
2
1 1

output
2
1
0

Note

In the first test case, a possible game with a score of $2$ is as follows:

Alice chooses the element $1$ . After this move, $a = [0, 0, 1]$ and $c = [1]$ .
Bob chooses the element $0$ . After this move, $a = [0, 1]$ and $c = [1]$ .
Alice chooses the element $0$ . After this move, $a = [1]$ and $c = [1, 0]$ .
Bob chooses the element $1$ . After this move, $a=[\,]$ and $c = [1, 0]$ .

At the end, $c = [1, 0]$ , which has a MEX of $2$ . Note that this is an example game and does not necessarily represent the optimal strategy for both players.

Formalize Description

给定 $1$ 个长度为 $n$ 的序列 $a$ ，Alice 与 Bob 轮流操作：

Alice：选择一个元素，放入数组 $c$ ，并将该元素在 $a$ 数组中删掉
Bob：选择一个元素，将该元素在 $a$ 数组中删掉

最后 $c$ 数组的最大的 $\mathrm{MEX}$ 是多少？

Solution

考虑 Bob 会如何删是最优的，可以发现如果有出现次数为 $1$ 的数，那么 Bob 一定会删掉出现次数为 $1$ 中最小的那个数。

证明：如果 Bob 删掉了一个出现次数 $\ge 1$ 的数，那么这时候，该数一定还存在，那么 Alice 就可以选择这个数，Bob 就等同于做了无用功。

所以，最终的答案应该是 $\min($ 最小的出现次数为 $1$ 的数，最小的出现次数为 $0$ 的数 $)$ ，如果两者都不存在，则输出 $n$ 。

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 2e5 + 10;

int n;
int a[N], cnt[N];

void solve() {
	cin >> n;

	for (int i = 0; i < n; i ++)
		cnt[i] = 0;
	for (int i = 1; i <= n; i ++)
		cin >> a[i], cnt[a[i]] ++;

	int one = 0;
	for (int i = 0; i < n; i ++)
		if (cnt[i] == 1) {
			if (one) {
				cout << i << endl;
				return;
			}
			one ++;
		} else if (cnt[i] == 0) {
			cout << i << endl;
			return;
		}
	cout << n << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

B. Non-Palindromic Substring

Problem Statement

A string $t$ is said to be $k$ -good if there exists at least one substring $^\dagger$ of length $k$ which is not a palindrome $^\ddagger$ . Let $f (t)$ denote the sum of all values of $k$ such that the string $t$ is $k$ -good.

You are given a string $s$ of length $n$ . You will have to answer $q$ of the following queries:

Given $l$ and $r$ ( $l < r$ ), find the value of $f(s_ls_{l + 1}\ldots s_r)$ .

$^\dagger$ A substring of a string $z$ is a contiguous segment of characters from $z$ . For example, “ $\mathtt{defor}$ ”, “ $\mathtt{code}$ ” and “ $\mathtt{o}$ ” are all substrings of “ $\mathtt{codeforces}$ ” while “ $\mathtt{codes}$ ” and “ $\mathtt{aaa}$ ” are not.

$^\ddagger$ A palindrome is a string that reads the same backwards as forwards. For example, the strings “ $\texttt{z}$ ”, “ $\texttt{aa}$ ” and “ $\texttt{tacocat}$ ” are palindromes while “ $\texttt{codeforces}$ ” and “ $\texttt{ab}$ ” are not.

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ( $\leq t \leq 2 \cdot 10^4$ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains two integers $n$ and $q$ ( $\le n \le 2 \cdot 10^5, 1 \le q \le 2 \cdot 10^5$ ), the size of the string and the number of queries respectively.

The second line of each test case contains the string $s$ . It is guaranteed the string $s$ only contains lowercase English characters.

The next $q$ lines each contain two integers, $l$ and $r$ ( $\le l < r \le n$ ).

It is guaranteed the sum of $n$ and the sum of $q$ both do not exceed $\cdot 10^5$ .

Output

For each query, output $f(s_ls_{l + 1}\ldots s_r)$ .

Example

input
5
4 4
aaab
1 4
1 3
3 4
2 4
3 2
abc
1 3
1 2
5 4
pqpcc
1 5
4 5
1 3
2 4
2 1
aa
1 2
12 1
steponnopets
1 12

output
9
0
2
5
5
2
14
0
2
5
0
65

Note

In the first query of the first test case, the string is $\mathtt{aaab}$ . $\mathtt{aaab}$ , $\mathtt{aab}$ and $\mathtt{ab}$ are all substrings that are not palindromes, and they have lengths $4$ , $3$ and $2$ respectively. Thus, the string is $2$ -good, $3$ -good and $4$ -good. Hence, $f(\mathtt{aaab}) = 2 + 3 + 4 = 9$ .

In the second query of the first test case, the string is $\mathtt{aaa}$ . There are no non-palindromic substrings. Hence, $f(\mathtt{aaa}) = 0$ .

In the first query of the second test case, the string is $\mathtt{abc}$ . $\mathtt{ab}$ , $\mathtt{bc}$ and $\mathtt{abc}$ are all substrings that are not palindromes, and they have lengths $2$ , $2$ and $3$ respectively. Thus, the string is $2$ -good and $3$ -good. Hence, $f(\mathtt{abc}) = 2 + 3 = 5$ . Note that even though there are $2$ non-palindromic substrings of length $2$ , we count it only once.

Formalize Description

给定一个长度为 $n$ 的字符串，接下来有 $q$ 次询问，每次询问给定 $l, r$ ，求出 $s_{l\sim r}$ 这个字符串中长度之和，使得该长度满足至少有 $1$ 个不是回文串的子串

Solution

Key Point: 观察性质是做这道题目最关键的一步

由于，如果所有子串都是回文串的情况极少，所以不妨探讨一下：

如果长度为偶数全都是回文串，则如果第 $i$ 位填了字符 $t$ ，那么第 $i + 1$ 位也一定是字符 $t$ ，因为长度为 $2$ 的要回文。所以，当且仅当整个串全部相同时，才会全都是回文串。
如果长度为奇数全都是回文串，那么字符全都相同显然仍为 $1$ 种情况；或者是 $a\ b\ a\ b$ 的形式也是可以的，即规定了前 $2$ 个字符，后面的字符可以相继推导出来，而这是交替的形式

综上所述，其实就这 $2$ 种情况，直接分类讨论判断即可。注意，如果这个序列本身是回文串，那么要先减掉这个序列的长度，判断某个序列是否为回文串用马拉车算法即可。

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 4e5 + 10;

int n, q;
string s;
int p[N], f1[N], f2[N];

void manacher(string ts) {
	int mr = 1, mid, m = ts.size() - 1;

	for (int i = 1; i <= m; i ++) {
		if (i < mr) p[i] = min(p[mid * 2 - i], mr - i);
		else p[i] = 1;
		while (ts[i - p[i]] == ts[i + p[i]]) p[i] ++;
		if (i + p[i] > mr) {
			mr = i + p[i];
			mid = i;
		}
	}
}

void solve() {
	cin >> n >> q >> s;

	string tmp;
	tmp += "$#";
	for (auto v : s)
		tmp += v, tmp += '#';
	tmp += '^', tmp = ' ' + tmp;
	s = ' ' + s;
	manacher(tmp);

	f1[n] = f2[n] = f2[n + 1] = n;
	for (int i = n - 1; i >= 1; i --) {
		f1[i] = s[i] == s[i + 1] ? f1[i + 1] : i;
		f2[i] = s[i] == s[i + 2] ? f2[i + 2] : i;
	}

	while (q --) {
		int l, r;
		cin >> l >> r;

		int res = (r - l + 3) * (r - l) / 2;
		if (p[l + r + 1] - 1 >= r - l + 1) res -= (r - l + 1);
		if ((r - l + 1) & 1) {
			if (f2[l] >= r && f2[l + 1] >= r - 1) res -= (r - l + 2) * ((r - l >> 1) - 1) / 2;
			if (f1[l] >= r) res -= (2 + r - l) * (r - l >> 1) / 2;
		} else {
			if (f2[l] >= r - 1 && f2[l + 1] >= r) res -= (3 + r - l) * (r - l - 1 >> 1) / 2;
			if (f1[l] >= r) res -= (1 + r - l) * (r - l - 1 >> 1) / 2;
		}

		cout << res << endl;
	}
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	cin >> dt;

	while (dt -- )
		solve();

	return 0;
}

C. Tree Compass

Problem Statement

You are given a tree with $n$ vertices numbered $\ldots, n$ . Initially, all vertices are colored white.

You can perform the following two-step operation:

Choose a vertex $v$ ( $\leq v \leq n$ ) and a distance $d$ ( $\leq d \leq n-1$ ).
For all vertices $u$ ( $\leq u \leq n$ ) such that $\text{dist}^\dagger(u,v)=d$ , color $u$ black.

Construct a sequence of operations to color all the nodes in the tree black using the minimum possible number of operations. It can be proven that it is always possible to do so using at most $n$ operations.

$^\dagger$ $\text{dist}(x, y)$ denotes the number of edges on the (unique) simple path between vertices $x$ and $y$ on the tree.

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ( $\leq t \leq 200$ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains a single integer $n$ ( $\le n \le 2 \cdot 10^3$ ) — the number of vertices of the tree.

The following $n - 1$ lines of each test case describe the edges of the tree. The $i$ -th of these lines contains two integers $u_i$ and $v_i$ ( $\le u_i, v_i \le n$ , $u_i \neq v_i$ ), the indices of the vertices connected by the $i$ -th edge.

It is guaranteed that the given edges form a tree.

It is guaranteed that the sum of $n$ over all test cases does not exceed $\cdot 10^3$ .

Output

For each test case, first output a single integer $o p$ $\le op \le n)$ , the minimum number of operations needed to color all vertices of the tree black.

Then, output $o p$ lines, each containing $2$ integers. The $i$ -th line should contain the values of $v$ and $d$ chosen for the $i$ -th operation ( $\le v \le n$ , $\le d \le n - 1$ )

You must guarantee that at the end of $o p$ operations, all vertices are colored black.

If there are multiple solutions, you may output any one of them.

Example

input
4
1
2
1 2
4
1 2
1 3
1 4
7
2 7
3 2
6 4
5 7
1 6
6 7

output
1
1 0
2
1 1
2 1
2
1 1
2 1
3
6 1
7 1
2 1

Note

In the first test case, there is only one possible operation, and performing it gives us a valid answer.

In the second test case, the first operation colors vertex $2$ black, and the second operation colors vertex $1$ black. It can be shown that it is impossible to color both vertices black in one operation, so the minimum number of operations needed is $2$ . Another possible solution is to use the $2$ operations: $(u, r) = (1, 0)$ and $(u, r) = (2, 0)$ .

In the third test case, the first operation colors vertices $2$ , $3$ and $4$ black, and the second operation colors vertex $1$ black. Again, it can be shown that it is impossible to color all vertices black in $1$ operation, so the minimum number of operations needed is $2$ .

In the fourth test case, the first operation colors vertices $4$ , $1$ and $7$ black, the second operation colors vertices $2$ , $5$ and $6$ black while the third operation colors vertices $3$ and $7$ black. Notice that it is allowed to color vertex $7$ black twice.

Thus, each node was marked at least once, with node $7$ marked twice. It can be shown that it is impossible to color all vertices black in fewer than $3$ moves.

Formalize Description

给定一棵 $n$ 个节点的树，每次可以将到某个节点距离全部相等的点涂黑，问最后全部点涂黑的方案数。

Solution

Key Point:

如果对于树的问题没有很好的思路，可以先考虑链的情况
树的问题如果不是 DP，那么就要考虑直径，中心，重心……

对于该题，如果是一条链，那么直接从中间的点向外依次不断涂黑即可。

那么，对于树的情况，链是中心，那树是不是也是其中一条链的中心呢？答案是直径的中心，因为当时直径的中心的时候，则操作数其实是直径的长度除 $2$ ，因为对于依次操作，其实是将以这个点为根的树某一层全部涂黑，所以直径中心是最优的。

不过，可能直径的长度为偶数，此时就需要另一种讨论。

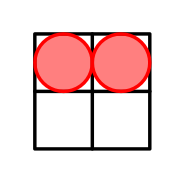
有时候，中间的 $2$ 个点都需要，比如说：
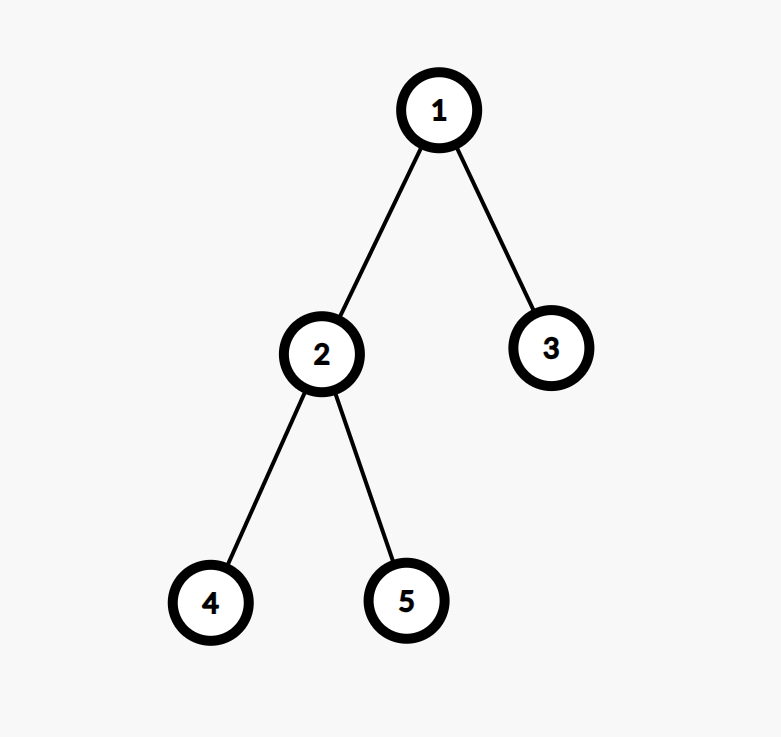
在这里插入图片描述

只用 $1$ 号点，答案应该是 $3$ ，但是如果按如下方式做，答案是 $2$
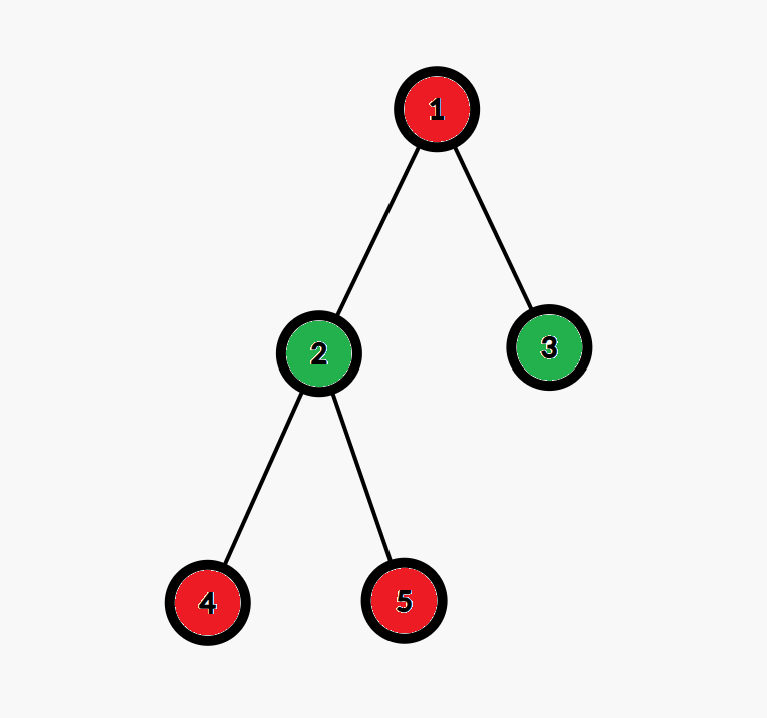
在这里插入图片描述

绿色点为 $1$ 号点图的，红色为 $2$ 号点图的。所以，其实每个点都将距离他为奇数的点涂掉即可。

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 2e3 + 10;

int n;
std::vector<int> G[N];
int dep[N], mx = -1, p[2], idx;
std::vector<int> path, res;

void dfs(int u, int fa) {
	if (dep[u] > mx)
		mx = dep[u], p[idx] = u;
	for (auto v : G[u]) {
		if (v == fa) continue;
		dep[v] = dep[u] + 1;
		dfs(v, u);
	}
}

void dfs2(int u, int fa) {
	path.emplace_back(u);
	if (u == p[1]) res = path;
	for (auto v : G[u]) {
		if (v == fa) continue;
		dfs2(v, u);
	}
	path.pop_back();
}

void solve() {
	cin >> n;

	for (int i = 1; i <= n; i ++)
		G[i].clear();
	path.clear(), idx = 0;

	int u, v;
	for (int i = 1; i < n; i ++)
		cin >> u >> v, G[u].emplace_back(v), G[v].emplace_back(u);

	mx = -1, dep[1] = 1, dfs(1, -1);
	mx = -1, dep[p[0]] = 1, dfs(p[idx ++], -1);
	path.emplace_back(0);
	dfs2(p[0], -1);

	if (mx & 1) {
		int mid = res[res.size() + 1 >> 1];
		int mxd = mx / 2;
		cout << mxd + 1 << endl;
		for (int i = 0; i <= mxd; i ++)
			cout << mid << " " << i << endl;
	} else {
		int mid1 = res[res.size() >> 1], mid2 = res[res.size() / 2 + 1];
		mx = -1, dep[mid1] = 1, dfs(mid1, -1);
		int mx1 = mx;
		mx = -1, dep[mid2] = 1, dfs(mid2, -1);
		int mx2 = mx;
		cout << mx1 / 2 + mx2 / 2 << endl;
		for (int i = 1; i < mx1; i += 2)
			cout << mid1 << " " << i << endl;
		for (int i = 1; i < mx2; i += 2)
			cout << mid2 << " " << i << endl;
	}
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}

D1. Counting Is Fun (Easy Version)

Problem Statement

This is the easy version of the problem. The only difference between the two versions is the constraint on $n$ . You can make hacks only if both versions of the problem are solved.

An array $b$ of $m$ non-negative integers is said to be good if all the elements of $b$ can be made equal to $0$ using the following operation some (possibly, zero) times:

Select two distinct indices $l$ and $r$ ( $\leq l \color{red}{<} r \leq m$ ) and subtract $1$ from all $b_i$ such that $\leq i \leq r$ .

You are given two positive integers $n$ , $k$ and a prime number $p$ .

Over all $k+1)^n$ arrays of length $n$ such that $\leq a_i \leq k$ for all $\leq i \leq n$ , count the number of good arrays.

Since the number might be too large, you are only required to find it modulo $p$ .

Input

Each test contains multiple test cases. The first line contains a single integer $t$ ( $\leq t \leq 10^3$ ) — the number of test cases. The description of the test cases follows.

The first line of each test case contains three positive integers $n$ , $k$ and $p$ ( $\leq n \leq 400$ , $\leq k \leq n$ , $10^8 < p < 10^9$ ) — the length of the array $a$ , the upper bound on the elements of $a$ and modulus $p$ .

It is guaranteed that the sum of $n^2$ over all test cases does not exceed $\cdot 10^5$ , and $p$ is prime.

Output

For each test case, on a new line, output the number of good arrays modulo $p$ .

Example

input
4
3 1 998244853
4 1 998244353
3 2 998244353
343 343 998244353

output
4
7
10
456615865

Note

In the first test case, the $4$ good arrays $a$ are:

$[0, 0, 0]$ ;
$[0, 1, 1]$ ;
$[1, 1, 0]$ ;
$[1, 1, 1]$ .

Formalize Description

称一个长度为 $n$ 的序列为好的，当且仅当这个序列可以通过每次将一个 不为 $1$ 的区间减 $1$ ，最终能减为全 $0$ 。问有多少个长度为 $n$ 的序列，每个数的范围为 $[0, k]$ ，使得该序列是好的。

Solution

一个序列是好的的充分必要条件为 $\forall i, a_i\le a_{i-1}+a_{i+1}$ 。

证明：

充分性：两边减的过程中，一定可以把 $a_i$ 也见到 $0$ 。

必要性：反证法，若存在某个好的序列，使得 $\exist i,a_i>a_{i-1}+a_{i+1}$ ，那么两边最终减到 $0$ 了之后， $a_i$ 还是有值的，但是不能减长度为 $1$ 的区间所以一定不是好的序列，与假设矛盾，证毕。

所以，只需判断有多少的序列满足这个条件即可。

$f_{i,j,k}$ 表示前 $i$ 个数，当前填 $j$ ，上一个位置填 $k$ 的方案数，则有： $f_{i,j,k}=\sum f_{i-1,k,t}[k\le j+t]$

这是 $O(n^4)$ 的，通过前缀和优化就可以达到 $O(n^3)$

Code

#include <bits/stdc++.h>
#define int long long

using namespace std;

typedef pair<int, int> PII;
typedef long long LL;

const int N = 4e2 + 10;

int n, k, p;
int f[2][N][N], g[2][N][N];

void add(int &a, int b) {
	a = (a + b + p) % p;
}

void solve() {
	cin >> n >> k >> p;

	for (int i = 0; i < 2; i ++)
		for (int j = 0; j <= k; j ++)
			for (int l = 0; l <= k; l ++)
				f[i][j][l] = g[i][j][l] = 0;
	for (int i = 0; i <= k; i ++)
		for (int j = 0; j <= k; j ++)
			if (i >= j) f[0][i][j] = 1, add(g[0][i][j], g[0][i][j - 1] + 1);
			else add(g[0][i][j], g[0][i][j - 1]);
	for (int i = 3; i <= n; i ++) {
		for (int j = 0; j <= k; j ++)
			for (int l = 0; l <= k; l ++)
				f[i & 1][j][l] = g[i & 1][j][l] = 0;
		for (int j = 0; j <= k; j ++)
			for (int l = 0; l <= k; l ++) {
				add(f[i & 1][j][l], g[(i & 1) ^ 1][l][k] - (l - j > 0 ? g[(i & 1) ^ 1][l][l - j - 1] : 0));
				add(g[i & 1][j][l], g[i & 1][j][l - 1] + f[i & 1][j][l]);
			}
	}

	int res = 0;
	for (int i = 0; i <= k; i ++)
		for (int j = 0; j <= k; j ++)
			if (j >= i)
				add(res, f[n & 1][i][j]);

	cout << res << endl;
}

signed main() {
	cin.tie(0);
	cout.tie(0);
	ios::sync_with_stdio(0);

	int dt;
	
	cin >> dt;

	while (dt --)
		solve();

	return 0;
}