文章目录
1. ML中为什么需要矩阵求导
简洁
用方程式表示如下:
y 1 = w 1 X 11 + w 2 X 12 (1) y_1=w_1X_{11}+w_2X_{12}\tag{1} y1=w1X11+w2X12(1)
y 2 = w 1 X 21 + w 2 X 22 (2) y_2=w_1X_{21}+w_2X_{22}\tag{2} y2=w1X21+w2X22(2)
转换成矩阵表示如下:
Y = X W (3) Y=XW\tag{3} Y=XW(3)
Y = [ y 1 y 2 ] , X = [ x 11 x 12 x 21 x 22 ] , W = [ w 1 w 2 ] (4) Y=\begin{bmatrix}y_1\\\\y_2\end{bmatrix},X=\begin{bmatrix}x_{11}&&x_{12}\\\\x_{21}&&x_{22}\end{bmatrix},W=\begin{bmatrix}w_{1}\\\\w_{2}\end{bmatrix}\tag{4} Y= y1y2 ,X= x11x21x12x22 ,W= w1w2 (4)快速
当使用python 中的numpy 库时候,在相对于 for 循环,Numpy 本身的计算提速相当快源代码
import time
import numpy as np
if __name__ == "__main__":
N = 1000000
a = np.random.rand(N)
b = np.random.rand(N)
start = time.time()
c = np.dot(a,b)
stop = time.time()
print(f"c={c}")
print("vectorized version: " + str(1000*(stop-start))+"ms")
c = 0
start1 = time.time()
for i in range(N):
c += a[i]*b[i]
stop1 = time.time()
print(f"c={c}")
print("for loop: " + str(1000*(stop1-start1))+"ms")
times1 = (stop1-start1)/(stop-start)
print(f"times1={times1}")
- 结果
c=250071.8870070607
vectorized version: 6.549358367919922ms
c=250071.88700706122
for loop: 265.43641090393066ms
times1=40.52861303239898# 向量化居然比单独的for循环快40倍
2. 向量函数与矩阵求导初印象
- 标量函数:输出为标量的函数
f ( x ) = x 2 ⇒ x ∈ R → x 2 ∈ R f(x)=x^2\Rightarrow x\in R\rightarrow x^2 \in R f(x)=x2⇒x∈R→x2∈R
f ( x ) = x 1 2 + x 2 2 ⇒ [ x 1 x 2 ] ∈ R 2 → x 1 2 + x 2 2 ∈ R f(x)=x_1^2+x_2^2\Rightarrow \begin{bmatrix}x_1\\\\x_2\end{bmatrix}\in R^2\rightarrow x_1^2+x_2^2 \in R f(x)=x12+x22⇒ x1x2 ∈R2→x12+x22∈R - 向量函数:输出为向量或矩阵的函数
<1> 输入标量,输出向量
f ( x ) = [ f 1 ( x ) = x f 2 ( x ) = x 2 ] ⇒ x ∈ R , [ x x 2 ] ∈ R 2 f(x)=\begin{bmatrix}f_1(x)=x\\\\f_2(x)=x^2\end{bmatrix}\Rightarrow x\in R,\begin{bmatrix}x\\\\x^2\end{bmatrix} \in R^2 f(x)= f1(x)=xf2(x)=x2 ⇒x∈R, xx2 ∈R2
<2> 输入标量,输出矩阵
f ( x ) = [ f 11 ( x ) = x f 12 ( x ) = x 2 f 21 ( x ) = x 3 f 22 ( x ) = x 4 ] ⇒ x ∈ R , [ x x 2 x 3 x 4 ] ∈ R 2 × 2 f(x)=\begin{bmatrix}f_{11}(x)=x&&f_{12}(x)=x^2\\\\f_{21}(x)=x^3&&f_{22}(x)=x^4\end{bmatrix}\Rightarrow x\in R,\begin{bmatrix}x&&x^2\\\\x^3&&x^4\end{bmatrix} \in R^{2\times2} f(x)= f11(x)=xf21(x)=x3f12(x)=x2f22(x)=x4 ⇒x∈R, xx3x2x4 ∈R2×2
<3> 输入向量,输出矩阵
f ( x ) = [ f 11 ( x ) = x 1 + x 2 f 12 ( x ) = x 1 2 + x 2 2 f 21 ( x ) = x 1 3 + x 2 3 f 22 ( x ) = x 1 4 + x 2 4 ] ⇒ [ x 1 x 2 ] ∈ R 2 , [ x 1 + x 2 x 1 2 + x 2 2 x 1 3 + x 2 3 x 1 4 + x 2 4 ] ∈ R 2 × 2 f(x)=\begin{bmatrix}f_{11}(x)=x_1+x_2&&f_{12}(x)=x_1^2+x_2^2\\\\f_{21}(x)=x_1^3+x_2^3&&f_{22}(x)=x_1^4+x_2^4\end{bmatrix}\Rightarrow \begin{bmatrix}x_1\\\\x_2\end{bmatrix} \in R^2,\begin{bmatrix}x_1+x_2&&x_1^2+x_2^2\\\\x_1^3+x_2^3&&x_1^4+x_2^4\end{bmatrix} \in R^{2\times2} f(x)= f11(x)=x1+x2f21(x)=x13+x23f12(x)=x12+x22f22(x)=x14+x24 ⇒ x1x2 ∈R2, x1+x2x13+x23x12+x22x14+x24 ∈R2×2 - 总结
矩阵求导的本质
d A d B = 矩阵 A 中的每个元素对矩阵 B 中的每个元素求导 \frac{\mathrm{d}A}{\mathrm{d}B}=矩阵A中的每个元素对矩阵B中的每个元素求导 dBdA=矩阵A中的每个元素对矩阵B中的每个元素求导
3. YX 拉伸术
3.1 f(x)为标量,X为列向量
- 标量不变,向量拉伸
- YX中,Y前面横向拉,X后面纵向拉
d f ( x ) d x , Y = f ( x ) 为标量, X = [ x 1 x 2 ⋮ x n ] 为列向量 \frac{\mathrm{d}f(x)}{\mathrm{d}x},Y=f(x)为标量,X=\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}为列向量 dxdf(x),Y=f(x)为标量,X= x1x2⋮xn 为列向量
f ( x ) = f ( x 1 , x 2 , . . . . , x n ) 为标量 f(x)=f(x_1,x_2,....,x_n)为标量 f(x)=f(x1,x2,....,xn)为标量 - 标量 f ( x ) f(x) f(x)不变,向量X 因为在YX拉伸术中在Y后面,所以向量X纵向拉伸,实际上就是将多元函数的偏导写在一个列向量中
d f ( x ) d x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dxdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)
3.2 f(x)为列向量,X 为标量
f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ] ; X 为标量 f(x)=\begin{bmatrix}f_1(x)\\\\f_2(x)\\\\\vdots\\\\f_n(x)\end{bmatrix};X 为标量 f(x)= f1(x)f2(x)⋮fn(x) ;X为标量
- 标量不变,向量拉伸
- YX中,Y前面横向拉,X后面纵向拉
d f ( x ) d x = [ ∂ f 1 ( x ) ∂ x ∂ f 2 ( x ) ∂ x … ∂ f n ( x ) ∂ x ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f_1(x)}{\partial x}&&\frac{\partial f_2(x)}{\partial x}&&\dots&&\frac{\partial f_n(x)}{\partial x}\end{bmatrix} dxdf(x)=[∂x∂f1(x)∂x∂f2(x)…∂x∂fn(x)]
3.3 f(x)为列向量,X 为列向量
f ( x ) = [ f 1 ( x ) f 2 ( x ) ⋮ f n ( x ) ] ; X = [ x 1 x 2 ⋮ x n ] 为列向量 f(x)=\begin{bmatrix}f_1(x)\\\\f_2(x)\\\\\vdots\\\\f_n(x)\end{bmatrix};X=\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}为列向量 f(x)= f1(x)f2(x)⋮fn(x) ;X= x1x2⋮xn 为列向量
- 第一步先固定Y ,将 X 纵向拉
d f ( x ) d x = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dxdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x) - 第二步,看每一个项 ∂ f ( x ) ∂ x 1 \frac{\partial f(x)}{\partial x_1} ∂x1∂f(x),其中f(x)为列向量, x 1 x_1 x1为标量,那么可以看出要进行 Y 横向拉
∂ f ( x ) ∂ x 1 = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 1 … ∂ f n ( x ) ∂ x 1 ] \frac{\partial f(x)}{\partial x_1}=\begin{bmatrix}\frac{\partial f_1(x)}{\partial x_1}&&\frac{\partial f_2(x)}{\partial x_1}&&\dots&&\frac{\partial f_n(x)}{\partial x_1}\end{bmatrix} ∂x1∂f(x)=[∂x1∂f1(x)∂x1∂f2(x)…∂x1∂fn(x)] - 第三步 ,将每项整合如下
d f ( x ) d x = [ ∂ f 1 ( x ) ∂ x 1 ∂ f 2 ( x ) ∂ x 1 … ∂ f n ( x ) ∂ x 1 ∂ f 1 ( x ) ∂ x 2 ∂ f 2 ( x ) ∂ x 2 … ∂ f n ( x ) ∂ x 2 ⋮ ⋮ … ⋮ ∂ f 1 ( x ) ∂ x n ∂ f 2 ( x ) ∂ x n … ∂ f n ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}x}=\begin{bmatrix}\frac{\partial f_1(x)}{\partial x_1}&&\frac{\partial f_2(x)}{\partial x_1}&&\dots&&\frac{\partial f_n(x)}{\partial x_1}\\\\\frac{\partial f_1(x)}{\partial x_2}&&\frac{\partial f_2(x)}{\partial x_2}&&\dots&&\frac{\partial f_n(x)}{\partial x_2}\\\\\vdots&&\vdots&&\dots&&\vdots\\\\\frac{\partial f_1(x)}{\partial x_n}&&\frac{\partial f_2(x)}{\partial x_n}&&\dots&&\frac{\partial f_n(x)}{\partial x_n}\end{bmatrix} dxdf(x)= ∂x1∂f1(x)∂x2∂f1(x)⋮∂xn∂f1(x)∂x1∂f2(x)∂x2∂f2(x)⋮∂xn∂f2(x)…………∂x1∂fn(x)∂x2∂fn(x)⋮∂xn∂fn(x)
4. 常见矩阵求导公式
4.1 Y = A T X Y=A^TX Y=ATX
f ( x ) = A T X ; A = [ a 1 , a 2 , … , a n ] T ; X = [ x 1 , x 2 , … , x n ] T , 求 d f ( x ) d X f(x)=A^TX;\quad A=[a_1,a_2,\dots,a_n]^T;\quad X=[x_1,x_2,\dots,x_n]^T,求\frac{\mathrm{d}f(x)}{\mathrm{d}X} f(x)=ATX;A=[a1,a2,…,an]T;X=[x1,x2,…,xn]T,求dXdf(x)
- 由于 A T = 1 × n , X = n × 1 , 那么 f ( x ) 为标量,即表示数值 A^T=1\times n,X=n\times1,那么f(x)为标量,即表示数值 AT=1×n,X=n×1,那么f(x)为标量,即表示数值,
- 标量不变,向量拉伸
- YX中,Y前面横向拉,X后面纵向拉
f ( x ) = ∑ i = 1 N a i x i f(x)=\sum_{i=1}^Na_ix_i f(x)=i=1∑Naixi
d f ( x ) d X = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dXdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x) - 可以计算 ∂ f ( x ) ∂ x i \frac{\partial f(x)}{\partial x_i} ∂xi∂f(x)
∂ f ( x ) ∂ x i = a i \frac{\partial f(x)}{\partial x_i}=a_i ∂xi∂f(x)=ai - 可得如下:
d f ( x ) d X = [ a 1 a 2 ⋮ a n ] = A \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}a_1\\\\a_2\\\\\vdots\\\\a_n\end{bmatrix}=A dXdf(x)= a1a2⋮an =A - 结论:
当 f ( x ) = A T X 当f(x)=A^TX 当f(x)=ATX
d f ( x ) d X = A \frac{\mathrm{d}f(x)}{\mathrm{d}X}=A dXdf(x)=A
4.2 Y = X T A X Y=X^TAX Y=XTAX
f ( x ) = X T A X ; A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a n 2 … a n n ] ; X = [ x 1 , x 2 , … , x n ] T , 求 d f ( x ) d X f(x)=X^TAX;\quad A=\begin{bmatrix}a_{11}&&a_{12}&&\dots&&a_{1n}\\\\a_{21}&&a_{22}&&\dots&&a_{2n}\\\\\vdots&&\vdots&&\dots&&\vdots\\\\a_{n1}&&a_{n2}&&\dots&&a_{nn}\end{bmatrix};\quad X=[x_1,x_2,\dots,x_n]^T,求\frac{\mathrm{d}f(x)}{\mathrm{d}X} f(x)=XTAX;A=
a11a21⋮an1a12a22⋮an2…………a1na2n⋮ann
;X=[x1,x2,…,xn]T,求dXdf(x)
f ( x ) = ∑ i = 1 N ∑ j = 1 N a i j x i x j f(x)=\sum_{i=1}^N\sum_{j=1}^Na_{ij}x_ix_j f(x)=i=1∑Nj=1∑Naijxixj
- 标量不变,YX拉伸术,X纵向拉伸
d f ( x ) d X = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix} dXdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x)
∂ f ( x ) ∂ x i = [ a i 1 a i 2 … a i n ] [ x 1 x 2 ⋮ x n ] + [ a 1 i a 2 i … a n i ] [ x 1 x 2 ⋮ x n ] \frac{\partial f(x)}{\partial x_i}=\begin{bmatrix}a_{i1}&a_{i2}&\dots&a_{in}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}+\begin{bmatrix}a_{1i}&a_{2i}&\dots&a_{ni}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix} ∂xi∂f(x)=[ai1ai2…ain] x1x2⋮xn +[a1ia2i…ani] x1x2⋮xn
d f ( x ) d X = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a n 2 … a n n ] [ x 1 x 2 ⋮ x n ] + [ a 11 a 21 … a n 1 a 12 a 22 … a n 2 ⋮ ⋮ … ⋮ a 1 n a 2 n … a n n ] [ x 1 x 2 ⋮ x n ] \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}a_{11}&a_{12}&\dots&a_{1n}\\\\a_{21}&a_{22}&\dots&a_{2n}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{n1}&a_{n2}&\dots&a_{nn}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}+\begin{bmatrix}a_{11}&a_{21}&\dots&a_{n1}\\\\a_{12}&a_{22}&\dots&a_{n2}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{1n}&a_{2n}&\dots&a_{nn}\end{bmatrix}\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix} dXdf(x)= a11a21⋮an1a12a22⋮an2…………a1na2n⋮ann x1x2⋮xn + a11a12⋮a1na21a22⋮a2n…………an1an2⋮ann x1x2⋮xn - 已知 A , A T A,A^T A,AT表示如下:
A = [ a 11 a 12 … a 1 n a 21 a 22 … a 2 n ⋮ ⋮ … ⋮ a n 1 a n 2 … a n n ] ; A T = [ a 11 a 21 … a n 1 a 12 a 22 … a n 2 ⋮ ⋮ … ⋮ a 1 n a 2 n … a n n ] A=\begin{bmatrix}a_{11}&a_{12}&\dots&a_{1n}\\\\a_{21}&a_{22}&\dots&a_{2n}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{n1}&a_{n2}&\dots&a_{nn}\end{bmatrix}\quad;A^T=\begin{bmatrix}a_{11}&a_{21}&\dots&a_{n1}\\\\a_{12}&a_{22}&\dots&a_{n2}\\\\\vdots&\vdots&\dots&\vdots\\\\a_{1n}&a_{2n}&\dots&a_{nn}\end{bmatrix} A= a11a21⋮an1a12a22⋮an2…………a1na2n⋮ann ;AT= a11a12⋮a1na21a22⋮a2n…………an1an2⋮ann - 综上所述如下:
当 f ( x ) = X T A X f(x)=X^TAX f(x)=XTAX时
d f ( x ) d X = A X + A T X = ( A + A T ) X \frac{\mathrm{d}f(x)}{\mathrm{d}X}=AX+A^TX=(A+A^T)X dXdf(x)=AX+ATX=(A+AT)X
5. 两种布局
5.1 概括
两种布局矩阵求导的本质是向量求导拉伸方向的区别,求导后元素排列不同
- 口诀:前面横向拉,后面纵向拉
- 分子布局 XY拉伸术 X Y \frac{X}{Y} YX,X横向拉,Y纵向拉
- 分母布局 YX拉伸术 Y X \frac{Y}{X} XY,Y横向拉,X纵向拉
5.2 举例
f ( x ) = X T X , X = [ x 1 x 2 … x n ] T f(x)=X^TX,X=\begin{bmatrix}x_1&x_2&\dots&x_n\end{bmatrix}^T f(x)=XTX,X=[x1x2…xn]T
- 分子布局,XY拉伸术,X横向拉,Y纵向拉,f(x)为标量,标量不变,X向量横向拉伸
d f ( x ) d X = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 … ∂ f ( x ) ∂ x n ] = [ 2 x 1 2 x 2 … 2 x n ] = 2 [ x 1 x 2 … x n ] = 2 X T \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}&\frac{\partial f(x)}{\partial x_2}&\dots&\frac{\partial f(x)}{\partial x_n}\end{bmatrix}=\begin{bmatrix}2x_1&2x_2&\dots&2x_n\end{bmatrix}=2\begin{bmatrix}x_1&x_2&\dots&x_n\end{bmatrix}=2X^T dXdf(x)=[∂x1∂f(x)∂x2∂f(x)…∂xn∂f(x)]=[2x12x2…2xn]=2[x1x2…xn]=2XT - 分母布局,YX拉伸术,Y横向拉,X纵向拉,f(x)为标量,标量不变,X向量纵向拉伸
d f ( x ) d X = [ ∂ f ( x ) ∂ x 1 ∂ f ( x ) ∂ x 2 ⋮ ∂ f ( x ) ∂ x n ] = [ 2 x 1 2 x 2 ⋮ 2 x n ] = 2 [ x 1 x 2 ⋮ x n ] = 2 X \frac{\mathrm{d}f(x)}{\mathrm{d}X}=\begin{bmatrix}\frac{\partial f(x)}{\partial x_1}\\\\\frac{\partial f(x)}{\partial x_2}\\\\\vdots\\\\\frac{\partial f(x)}{\partial x_n}\end{bmatrix}=\begin{bmatrix}2x_1\\\\2x_2\\\\\vdots\\\\2x_n\end{bmatrix}=2\begin{bmatrix}x_1\\\\x_2\\\\\vdots\\\\x_n\end{bmatrix}=2X dXdf(x)= ∂x1∂f(x)∂x2∂f(x)⋮∂xn∂f(x) = 2x12x2⋮2xn =2 x1x2⋮xn =2X - 综上所述: 分子布局 = ( 分母布局 ) T 分子布局=(分母布局)^T 分子布局=(分母布局)T
6. 最小二乘法-分母布局
- 需要拟合一个线,使得线距离每个点的距离和最短。

L ( b ) = ∑ i = 1 ( y i − x i b i ) 2 L(b)=\sum_{i=1}(y_i-x_ib_i)^2 L(b)=i=1∑(yi−xibi)2 - 为了方便计算,需将以上求和公式改为矩阵形式如下
Y = [ y 1 y 2 … y n ] T ; X = [ x 1 T x 2 T … x n T ] T ; x i T = [ x i 1 x i 2 … x i n ] Y=\begin{bmatrix}y_1&y_2&\dots&y_n\end{bmatrix}^T;\quad X=\begin{bmatrix}x_1^T&x_2^T&\dots&x_n^T\end{bmatrix}^T;\quad x_i^T=\begin{bmatrix}x_{i1}&x_{i2}&\dots&x_{in}\end{bmatrix} Y=[y1y2…yn]T;X=[x1Tx2T…xnT]T;xiT=[xi1xi2…xin]
L ( b ) = ( Y − X b ) T ( Y − X b ) L(b) = (Y-Xb)^T(Y-Xb) L(b)=(Y−Xb)T(Y−Xb)
= ( Y T − b T X T ) ( Y − X b ) = Y T Y − Y T X b − b T X T Y + b T X T X b \quad=(Y^T-b^TX^T)(Y-Xb)=Y^TY-Y^TXb-b^TX^TY+b^TX^TXb =(YT−bTXT)(Y−Xb)=YTY−YTXb−bTXTY+bTXTXb - 因为 Y T X b Y^TXb YTXb为标量,所以 Y T X b = b T X T Y Y^TXb=b^TX^TY YTXb=bTXTY
L ( b ) = Y T Y − 2 Y T X b + b T X T X b L(b) =Y^TY-2Y^TXb+b^TX^TXb L(b)=YTY−2YTXb+bTXTXb - 求 L ( b ) L(b) L(b)对b求导可得如下:
d Y T Y d ( b ) = [ 0 0 ⋮ 0 ] n × 1 \frac{\mathrm{d}Y^TY}{\mathrm{d}(b)}=\begin{bmatrix}0\\\\0\\\\\vdots\\\\0\end{bmatrix}_{n\times1} d(b)dYTY= 00⋮0 n×1 - 因为 d A T X d ( X ) = A \frac{\mathrm{d}A^TX}{\mathrm{d}(X)}=A d(X)dATX=A可得如下:
d 2 Y T X b d ( b ) = ( 2 Y T X ) T = 2 X T Y \frac{\mathrm{d}2Y^TXb}{\mathrm{d}(b)}=(2Y^TX)^T=2X^TY d(b)d2YTXb=(2YTX)T=2XTY - 因为 d X T A X d ( X ) = ( A + A T ) X , 可得如下: \frac{\mathrm{d}X^TAX}{\mathrm{d}(X)}=(A+A^T)X,可得如下: d(X)dXTAX=(A+AT)X,可得如下:
d b T X T X b d ( b ) = ( X T X + ( X T X ) T ) b = 2 X T X b \frac{\mathrm{d}b^TX^TXb}{\mathrm{d}(b)}=(X^TX+(X^TX)^T)b=2X^TXb d(b)dbTXTXb=(XTX+(XTX)T)b=2XTXb - 综上所述可得如下:
d L ( b ) d ( b ) = − 2 X T Y + 2 X T X b = 0 \frac{\mathrm{d}L(b)}{\mathrm{d}(b)}=-2X^TY+2X^TXb=0 d(b)dL(b)=−2XTY+2XTXb=0
b ^ = ( X T X ) − 1 X T Y \hat{b}=(X^TX)^{-1}X^TY b^=(XTX)−1XTY




























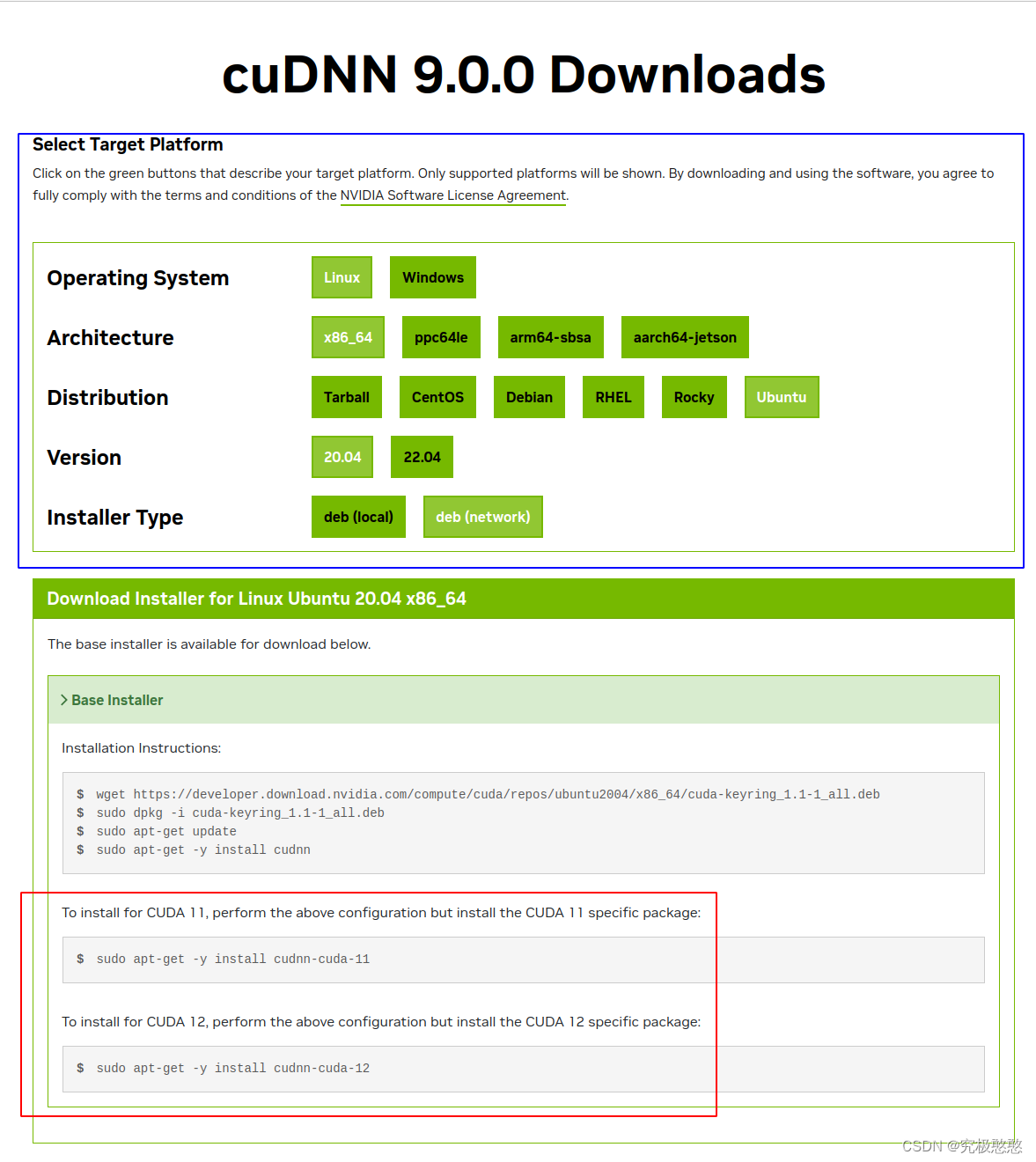


![C++初阶 | [九] list 及 其模拟实现](https://img-blog.csdnimg.cn/direct/f04a8b16b8b74a128abddddb0461f4ac.png)



