最短路
基本
最短路可以认为是图论最基础的内容之一,涉及到的算法也很多。为了方便,假设图有 n n n 个点, m m m 条边, ( u , v ) (u,v) (u,v) 这条边的边权用 w ( u , v ) w(u,v) w(u,v) 表示。
性质
有几条关于边权为正的图的最短路的性质:
- 任意两点之间的最短路,不会经过重复的点和边。
- 任意两点之间的最短路,结点数不会超过 n n n,边数不会超过 n − 1 n-1 n−1。
对于前者,由于边权为正,如果一条最短路需要经过重复的点或边,更优的做法显然是在第一次经过这个点或者边时就按照第二次乃至更多次从这个点或边离开时的路径直接离开,继续往后走。
对于后者,显然如果你经过了 n + 1 n+1 n+1 个点,就说明重复经过了点,回到了第一条性质;经过最短路上的 x x x 个点显然用 x − 1 x-1 x−1 条边就够了,由于边权为正,多经过一条边都是不优的。
Floyd
一个基于动态规划的 O ( n 3 ) O(n^3) O(n3) 最短路算法,实现简单,可以求出原图中任意两点之间的最短路。只要最短路存在( u , v u,v u,v 之间不存在一条可以到达一个负环的路径),Floyd 都能跑。
令 f k , i . j f_{k,i.j} fk,i.j 表示从 i i i 到 j j j 在只经过前 1 1 1 至 k k k 个点时 i , j i,j i,j 的最短路。如果原图中 u , v u,v u,v 有连边,则 f 0 , u , v ← w ( u , v ) f_{0,u,v}\gets w(u,v) f0,u,v←w(u,v),否则 f 0 , u , v ← + ∞ f_{0,u,v}\gets+\infty f0,u,v←+∞,表示当前情况下 u , v u,v u,v 不存在最短路。特别的, f 0 , u , u ← 0 f_{0,u,u}\gets0 f0,u,u←0,显然自己到自己不用走任何路。
转移过程中,先从小到大枚举 k k k,再枚举两个点 i , j i,j i,j, min ( f k − 1 , i , j , f k − 1 , i , k + f k − 1 , k , j ) → f k , i , j \min(f_{k-1,i,j},f_{k-1,i,k}+f_{k-1,k,j})\to f_{k,i,j} min(fk−1,i,j,fk−1,i,k+fk−1,k,j)→fk,i,j。其中 f k − 1 , i , j f_{k-1,i,j} fk−1,i,j 表示 i , j i,j i,j 不经过 k k k 的最短路, f k − 1 , i , k + f k − 1 , k , j f_{k-1,i,k}+f_{k-1,k,j} fk−1,i,k+fk−1,k,j 表示经过 k k k,将 k k k 作为 i → k i\to k i→k 和 k → j k\to j k→j 两条最短路的中转点,尝试用这首尾相连的两条最短路更新 i , j i,j i,j 之间的最短路。
最后 u , v u,v u,v 之间的最短路即为 f n , u , v f_{n,u,v} fn,u,v,即允许经过所有点时 u , v u,v u,v 的最短路。不过这么做的空间复杂度是 O ( n 3 ) O(n^3) O(n3) 的。观察转移方程发现:对于任意 u , v , k u,v,k u,v,k, f k , u , v f_{k,u,v} fk,u,v 的值不会受 f k + 1 , u , v f_{k+1,u,v} fk+1,u,v 及以上的值的影响。所以我们可以把 k k k 这一维压缩掉,空间复杂度 O ( n 2 ) O(n^2) O(n2),时间复杂度 O ( n 3 ) O(n^3) O(n3)。
const int maxn = 305,inf = 1e9; // “无穷大”的值依据题目边权大小而定。
int f[maxn][maxn],w[maxn][maxn],n;
void Floyd() {
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= n;j ++)
if (i == j) f[i][j] = 0;
else f[i][j] = w[i][j]; // i,j不连通则w[i][j]=inf;
for (int k = 1;k <= n;k ++)
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= n;j ++)
f[i][j] = min(f[i][j],f[i][k] + f[k][j]);
}
int Query(int u,int v) { return f[u][v]; }
不过麻雀虽小,五脏俱全。Floyd 能干的事情远不止最短路,最小环、传递闭包、连通性等等都能做,不在此论述。
Dijkstra
好好看看你们有木有拼错这个单词:(
一个基于松弛操作的单源最短路径算法,即以某一个点为起点,可以计算该点到其他所有点的最短路径。但是只适用于非负边权的图。
什么是松弛操作?我们钦定起点为 S S S,令 d i s x dis_x disx 表示当前计算出的从 S S S 到 x x x 的最短路。对于 ( u , v ) (u,v) (u,v) 这条边,松弛操作就是 d i s v ← min ( d i s v , d i s u + w ( u , v ) ) dis_v\gets\min(dis_v,dis_u+w(u,v)) disv←min(disv,disu+w(u,v)),意思是尝试用 S → u S\to u S→u 的最短路再多走 ( u , v ) (u,v) (u,v) 这条边组成的路径更新 S → v S\to v S→v 的最短路。
在 Dijkstra 中,初始化 d i s S ← 0 dis_S\gets0 disS←0,其他点的 d i s dis dis 均设为 + ∞ +\infty +∞,表示当前没有计算出 S S S 到该点的最短路。我们将所有点分为两个点集:已经确定最短路长度的点集、未确定最短路长度的点集。一开始所有点都默认属于后者(包括 S S S)。
每次我们从未确定最短路长度的点集中取出一个 d i s dis dis 最小的点 u u u(最开始就会选择 S S S),将 u u u 加入已经确定最短路长度的点集;对于一条边 ( u , v ) (u,v) (u,v) ,对 u , v u,v u,v 执行松弛操作,即 d i s v ← min ( d i s v , d i s u + w ( u , v ) ) dis_v\gets\min(dis_v,dis_u+w(u,v)) disv←min(disv,disu+w(u,v))。一直到所有点都确定了最短路长度为止。此时 S → u S\to u S→u 的最短路径长度就是 d i s u dis_u disu。
为什么每次选取一个 d i s dis dis 最小的点?
对于 ( x , v ) (x,v) (x,v) 和 ( y , v ) (y,v) (y,v) 这两条边,假设 w ( x , v ) = w ( y , v ) w(x,v)=w(y,v) w(x,v)=w(y,v),那么选取 d i s dis dis 更小的点去更新 d i s v dis_v disv 显然是更优的。所以每次选取 d i s dis dis 最小的还没确定最短路的点,相当于选取了一个最有潜力的点,用它去松弛其他点的效果总是较好的。
按照上文的选取方法,为什么每个点被用于松弛其他点一次之后就不再用于松弛了?(怎么保证某个点的最短路是否确定?)
这就提到了 Dijkstra 的限制条件,也是 Dijkstra 的复杂度保证——只适用于非负边权的图。
“不再被用于松弛”是因为自身的 d i s dis dis 不会再被更新。假设 u u u 点已经被加入已经确定最短路长度的点集,但在后面又被 v v v 点松弛,因为 w ( u , v ) > 0 w(u,v)>0 w(u,v)>0(松弛操作成功了所以边权不会为 0 0 0),说明 d i s v < d i s u dis_v<dis_u disv<disu,如果 d i s v dis_v disv 的这个值不在 d i s u dis_u disu 被计算之后,按照算法流程, v v v 会优先被选取( d i s v < d i s u dis_v<dis_u disv<disu,潜力更大), u u u 还没加入已经确定最短路长度的点集就被 v v v 松弛了。
如果 d i s v dis_v disv 的这个值在 d i s u dis_u disu 被计算之后才被计算出来,按照边权非负, d i s v dis_v disv 的值一定会比 d i s u dis_u disu 大,与之前矛盾了。所以每个点至多只会被用来松弛一次。这也是朴素 Dijkstra 算法 O ( n 2 ) O(n^2) O(n2) 时间复杂度的原因,即至多发生 n n n 次松弛操作,找 d i s dis dis 最小的点是 O ( n ) O(n) O(n) 的(后续优化也主要针对它),总时间复杂度 O ( n + m ) n = O ( n 2 ) O(n+m)n=O(n^2) O(n+m)n=O(n2)(默认 n , m n,m n,m 同阶)。
针对“寻找 d i s dis dis 最小的在未确定最短路长度的点集中的点”这个过程,有两个主流的实现方法:(来源于oi-wiki)
- 手写堆:每次成功松弛一条边 ( u , v ) (u,v) (u,v),就将 v v v 插入二叉堆中(如果 v v v 已经在二叉堆中,直接修改相应元素的权值即可),每次取 d i s dis dis 最小的点直接取出堆顶即可。至多进行 m m m 次插入(或修改)操作,至多 n n n 次删除操作,二叉堆中最多待 n n n 个点,操作复杂度即为 O ( log n ) O(\log n) O(logn),总时间复杂度 O ( ( n + m ) log n ) = O ( m log n ) O((n+m)\log n)=O(m\log n) O((n+m)logn)=O(mlogn)。
STL优先队列:最常用的写法之一。和手写二叉堆类似,但如果同一个点的最短路径被多次松弛,已经在优先队列中但 d i s dis dis 值还未被更新的该点没办法修改其 d i s dis dis 值,只能继续呆在优先队列中,所以队列里最多会有 m m m 个点,每成功一次松弛操作就要新加一个点。时间复杂度 O ( m log m ) O(m\log m) O(mlogm)。
这里采用的是第二个实现方法。
#define mk make_pair
const int maxn = 1e5 + 5, maxm = 2e6 + 5;
// 采用链式前向星存图,邻接表同理。
struct Edge { int v,w,nxt; } e[maxm];
int head[maxn],cnt;
void addEdge(int u,int v,int w) {
e[++ cnt] = Edge{v,w,head[u]};
head[u] = cnt;
}
int dis[maxn]; bool vis[maxn]; // 最短路长度,及标记是否已经被确定最短路。
void Dijkstra(int S) {
memset(dis,0x3f,sizeof(dis)); // 初始化无穷大
dis[S] = 0;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
// x.second表示点的编号,x.first表示x.second在放进优先队列时dis[x.second]的大小。
q.push(mk(0,S));
while (!q.empty()) {
pair<int,int> top = q.top(); q.pop();
int u = top.second;
if (vis[u]) continue; // 已经被确定了,由于优先队列中会有点编号相同的元素特判一下。
vis[u] = true;
for (int i = head[u];i;i = e[i].nxt) {
int v = e[i].v, w = e[i].w;
if (dis[v] > dis[u] + w) { // 松弛操作
dis[v] = dis[u] + w;
if (!vis[v]) q.push(mk(dis[v],v));
}
}
}
}
一定注意只适用于非负边权的图!
BellanFord / SPFA
也许你更多听到的是 SPFA 这个名字。SPFA 算法可以说是对于 BellanFord 算法的一个优化。对于为什么说 SPFA 已经死了,现在你胆敢在没有负权边的图上跑 SPFA,就可以 AFO( Away from OI \texttt{Away from OI} Away from OI)了。在 P4779 【模板】单源最短路径(标准版) 中有这么一段话:
2018 年 7 月 19 日,某位同学在 NOI Day 1 T1 归程 一题里非常熟练地使用了一个广为人知的算法求最短路。
然后呢?
100 → 60 100 \rightarrow 60 100→60;
Ag → Cu \text{Ag} \rightarrow \text{Cu} Ag→Cu;
最终,他因此没能与理想的大学达成契约。
小 F 衷心祝愿大家不再重蹈覆辙。
可见出题人们的责任心之强。
回到正题。BellanFord 也是基于松弛操作实现的,但它能跑负边权。相较于 Dijkstra 每个点的出边只会松弛一次,BellanFord 每次都把 m m m 条边全部松弛一遍,直到无法再进行松弛。
这就解决了负权的问题:假设最短路存在(没有负环),那么如果有一个点通过负权边使最短路变短了,那么其出边就可能成功松弛。那么这样 O ( m ) O(m) O(m) 的松弛操作至多进行几次呢?
由于当图中每条边都无法被松弛时, S S S 到每个点的最短路就被确定了。换而言之,当松弛操作成功时,某一条最短路就会多一条边。所以每一轮对所有边的松弛操作至少会使最短路的边数加一,严谨证明略,可以简单地手模一下。
根据开头提到的最短路边数不会超过 n − 1 n-1 n−1,所以当最短路存在时这样的松弛操作至多进行 n − 1 n-1 n−1 轮。所以总时间复杂度 O ( n m ) O(nm) O(nm)。
因为 BellanFord 能跑负边权,且由于它独特的松弛方法,它可以用来判断是否有负环(最短路是否存在)。上文提到如果最短路存在松弛操作至多进行 n − 1 n-1 n−1 轮,如果能到达一个负环上,那么就可以在负环上永远跑下去使最短路越来越短,松弛操作也永无休止。
所以当松弛操作进行到第 n n n 轮时仍有边可以松弛,则说明当前以 S S S 为起点时存在负环。这就可以判断负环了,实现也很简单。注意:有可能图中存在负环但从 S S S 出发无法到达,所以应该建一个超级源点向所有点连一条边权为 0 0 0 的单向边,从这个超级源点出发跑最短路。这也是查询最短的任意两点间最短路的方法。
struct Edge { int u, v, w; }; // 存每条边
vector<Edge> mp;
int dis[maxn], u, v, w;
const int inf = 0x3f3f3f3f;
bool BellanFord(int n, int s) { // 顺便返回当前是否存在负环。
memset(dis, 0x3f, sizeof(dis));
dis[s] = 0;
bool flag = false; // 判断一轮循环过程中是否发生松弛操作。
for (int i = 1; i <= n; i++) {
flag = false;
for (int j = 0; j < mp.size(); j++) {
u = mp[j].u, v = mp[j].v, w = mp[j].w;
if (dis[u] == inf) continue;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
flag = true;
}
}
// 没有可以松弛的边时就停止算法。
if (!flag) break;
}
// 第n轮循环仍然可以松弛时说明s点可以抵达一个负环。
return flag;
}
然后介绍 SPFA。显然 ( u , v ) (u,v) (u,v) 这条边可能可以被二次松弛成功,当且仅当 d i s u dis_u disu 变得更小。所以我们可以开一个队列,记录每一轮 d i s dis dis 被更新过的点,下一轮就用这些点的出边继续松弛。不过在当今社会,基本可以认为它的复杂度仍然为 O ( n m ) O(nm) O(nm)。且用且谨慎
struct Edge { int v, w; };
vector<Edge> e[maxn];
int dis[maxn], cnt[maxn], vis[maxn];
queue<int> q;
bool SPFA(int n, int s) {
memset(dis, 63, sizeof(dis));
dis[s] = 0, vis[s] = 1;
q.push(s);
while (!q.empty()) { // 可以发现和Dijkstra的堆优化版本挺像的,不过Dijkstra中每个点不会被重复松弛。
int u = q.front();
q.pop(); vis[u] = 0;
for (auto V : e[u]) {
int v = V.v, w = V.w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
cnt[v] = cnt[u] + 1;
if (cnt[v] >= n) return false;
if (!vis[v]) { q.push(v); vis[v] = 1 };
}
}
}
return true;
}
例题
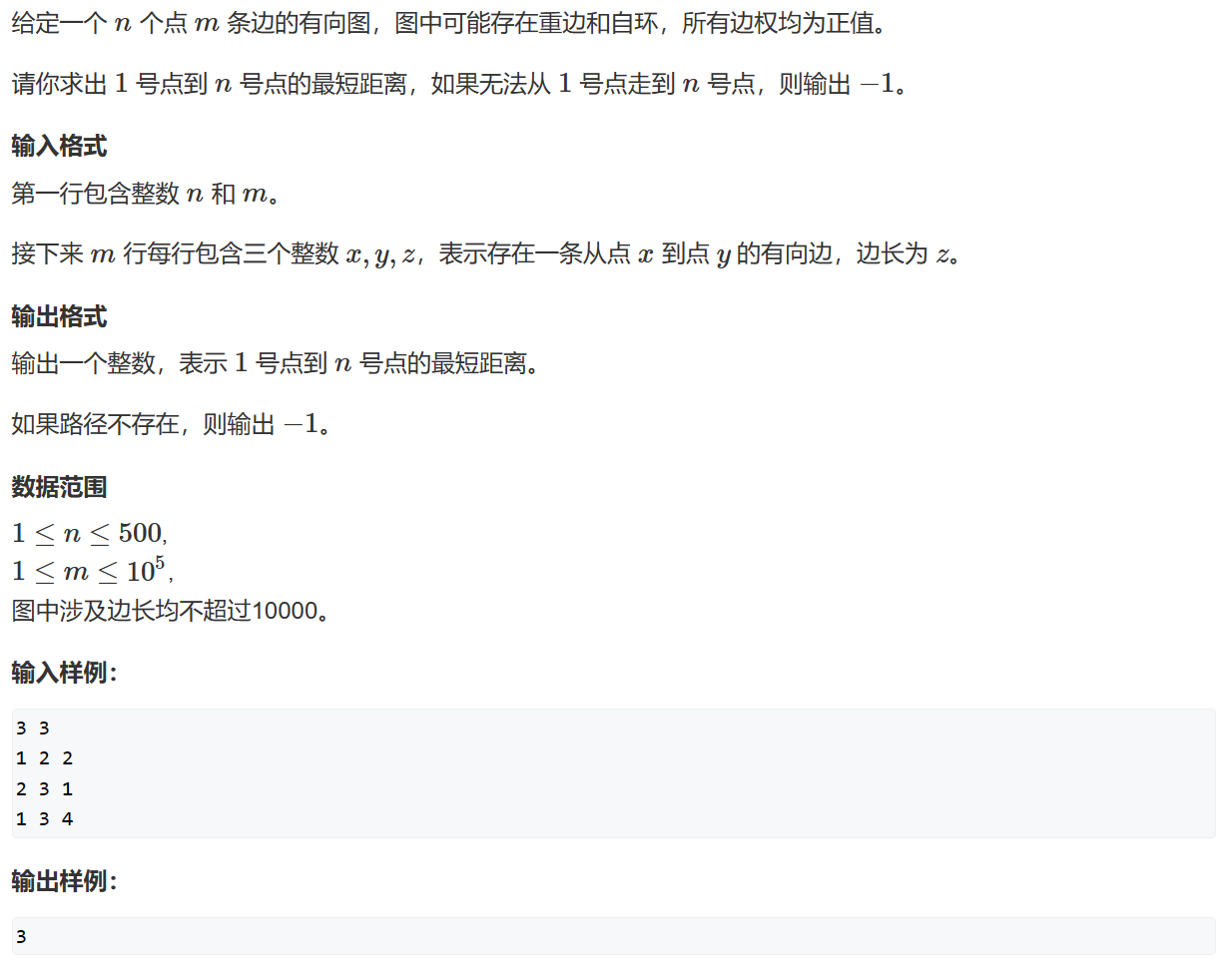
模板题
再次鞭策SPFA按照上文写就行。
中等题
- P4880 抓住czx 绿题
如果 lty 从起点出发,发现在到达 e e e 点之前 czx 已经逃逸了(即从 b b b 出发到达 e e e 所用时间小于 a 1 a_1 a1),因为我们知道 czx 什么时候瞬移,所以 lty 只能考虑去到 czx 第二次瞬移前待的点。后面的情况以此类推。
所以我们可以算出以 b b b 为起点到达其他点的最短路,设从 b b b 到 x x x 的最短路为 d i s x dis_x disx,并将 a a a 和对应的 x x x 按照 a a a 从小到大排序。对于每个 a i , x a_i,x ai,x,如果 d i s x < a i + 1 dis_x<a_{i+1} disx<ai+1,即 lty 可以在 czx 瞬移前赶到 x x x 并且等着 czx 过来(或者直接逮走),则说明此时的 max ( a i , d i s x ) \max(a_i,dis_x) max(ai,disx) 即为一个可能的用时(注意既有可能是 czx 等着 lty 走过来,也有可能是 lty 等着 czx 瞬移)。
最后特判一下 czx 停止瞬移后 lty 才能赶到的情况即可。
#include<bits/stdc++.h>
#define mk make_pair
using namespace std;
const int maxn = 1e5 + 5;
int n,m,b,e,dis[maxn],T,ans = 2e9; bool vis[maxn];
vector<pair<int,int> > mp[maxn];
pair<int,int> czx[maxn];
void addEdge(int u,int v,int w) {
mp[u].push_back(mk(v,w));
mp[v].push_back(mk(u,w));
}
void Dijkstra() {
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
memset(dis,0x3f,sizeof(dis));
dis[b] = 0; q.push(mk(0,b));
while (!q.empty()) {
auto now = q.top(); q.pop();
int u = now.second;
if (vis[u]) continue;
vis[u] = true;
for (auto V : mp[u]) {
int v = V.first, w = V.second;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (!vis[v]) q.push(mk(dis[v],v));
}
}
}
}
int main() {
scanf("%d%d%d%d",&n,&m,&b,&e);
for (int i = 1,u,v,w;i <= m;i ++) {
scanf("%d%d%d",&u,&v,&w);
addEdge(u,v,w);
}
Dijkstra(); scanf("%d",&T);
for (int i = 1;i <= T;i ++) scanf("%d%d",&czx[i].first,&czx[i].second);
sort(czx + 1,czx + T + 1);
int lstT = 0,lstP = e;
for (int i = 1,t,x;i <= T;i ++) {
t = czx[i].first, x = czx[i].second;
if (dis[lstP] < t) ans = min(ans,max(lstT,dis[lstP]));
lstT = t, lstP = x;
}
ans = min(ans,max(lstT,dis[lstP]));
printf("%d",ans);
return 0;
}
这题有 dp、线段树等其他做法,但这里介绍最短路做法。我都为这种方法震惊
题目要求用若干个区间覆盖完整个大区间,可以抽象理解成把区间当作若干条路径,代价即为边权,最终使得大区间的开头能够走到区间结尾即可。
对于两个区间 [ l 1 , r 1 ] , [ l 2 , r 2 ] [l1,r1],[l2,r2] [l1,r1],[l2,r2],如果我们让边直接为 ( l 1 , r 1 ) , ( l 2 , r 2 ) (l1,r1),(l2,r2) (l1,r1),(l2,r2),那么就处理不了形如 r 1 = l 2 − 1 r1=l2-1 r1=l2−1 的情况(两个区间不相交但中间无空隙)。所以我们将每个区间的末尾加一作为边的终点(即建形如 ( l 1 , r 1 + 1 ) (l1,r1+1) (l1,r1+1) 这样的边),最终判断区间开头是否和区间末尾加一连通即可。
如何处理相交区间呢?显然可以用两个相交区间的并覆盖大区间的一个部分,但这么直接建图显然做不到。抽象理解一下,两个相交区间 [ l 1 , r 1 ] , [ l 2 , r 2 ] [l1,r1],[l2,r2] [l1,r1],[l2,r2]( l 2 ≤ r 1 l2\leq r1 l2≤r1),相当于先从 l 1 l1 l1 走到了 r 1 r1 r1,再往回走一段到达 l 2 l2 l2,最后走到 r 2 r2 r2。所以有一个直接想法:每两个相交的区间,都将其中靠后的一个区间结尾向另一个靠前的区间开头连边,即连一条形如 ( r 1 , l 2 ) (r1,l2) (r1,l2) 的边。
但这样的复杂度显然不允许(最坏情况下 O ( n 2 ) O(n^2) O(n2))。再细想一下,我们可以把 ( r 1 , l 2 ) (r1,l2) (r1,l2) 这条边拆成 ( r 1 , r 1 − 1 ) , ( r 1 − 1 , r 1 − 2 ) , … , ( l 2 + 1 , l 2 ) (r1,r1-1),(r1-1,r1-2),\dots,(l2+1,l2) (r1,r1−1),(r1−1,r1−2),…,(l2+1,l2) 这么多条边,其他区间也可以用这么多边,而且不会影响不相交区间之间的连通性。
于是正解思路就出来了:一开始我们连 E − M + 1 E-M+1 E−M+1 条形如 ( i + 1 , i ) (i+1,i) (i+1,i) 的边权为 0 0 0 的边,直接先人一步把可能需要连的边全部连好。为什么把所有这样的边都连好不会影响答案?即使你可以通过这些边往回走,但你的最终目标是 M + 1 M+1 M+1 这个终点(实现中所有区间末尾都会被加一),且这些边边权为 0 0 0,不会影响答案。
然后按照上文方法建边,以 E E E 为起点跑一遍最短路,如果 d i s M + 1 dis_{M+1} disM+1 不是 + ∞ +\infty +∞ 即连通则有解,答案即为 d i s M + 1 dis_{M+1} disM+1。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 10005,maxm = 1e5 + 5;
vector<pair<int,int> > mp[maxm];
void addEdge(int u,int v,int w) { mp[u].push_back({v,w}); }
int n,s,t,dis[maxm]; bool vis[maxm];
int main() {
scanf("%d%d%d",&n,&s,&t);
for (int i = t + 1;i > s;i --)
addEdge(i,i - 1,0);
for (int i = 1,u,v,w;i <= n;i ++) {
scanf("%d%d%d",&u,&v,&w);
addEdge(u,v + 1,w);
}
// 此题无负权边所以使用Dijkstra。
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > q;
memset(dis,0x3f,sizeof(dis));
dis[s] = 0; q.push({0,s});
while (!q.empty()) {
int u = q.top().second; q.pop();
if (vis[u]) continue;
vis[u] = true;
for (auto V : mp[u]) {
int v = V.first, w = V.second;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (!vis[v]) q.push({dis[v],v});
}
}
}
if (dis[t + 1] == 0x3f3f3f3f) dis[t + 1] = -1;
printf("%d",dis[t + 1]);
return 0;
}
把每个格子都视作图上的一个点,坐标相邻的点之间的点连边。设从 ( u , v ) (u,v) (u,v) 向相邻的格子 ( x , y ) (x,y) (x,y) 连边,则边权即为将 ( u , v ) (u,v) (u,v) 上的箭头对准 ( x , y ) (x,y) (x,y) 所花的代价。然后跑最短路就行了,注意没有箭头的点不能有出边。
#include<bits/stdc++.h>
#define mk make_pair
#define type pair<int,pair<int,int> >
using namespace std;
const int maxn = 505;
int n,m,yt[maxn][maxn],dis[maxn][maxn];
char mg[maxn][maxn]; bool vis[maxn][maxn];
vector<pair<pair<int,int>,int> > mp[maxn][maxn];
void addEdge(int ux,int uy,int vx,int vy,int w) {
mp[ux][uy].push_back(mk(mk(vx,vy),w));
}
int getnum(int x,int y) {
char now = mg[x][y];
if (now == 'N') return 0;
if (now == 'E') return 1;
if (now == 'S') return 2;
if (now == 'W') return 3;
return -1;
}
int turn(int now,int tg) {
if (now > tg) return 4 + tg - now;
return tg - now;
}
void Dijkstra() {
priority_queue<type,vector<type>,greater<type> > q;
memset(dis,0x3f,sizeof(dis));
q.push(mk(0,mk(1,1))); dis[1][1] = 0;
while (!q.empty()) {
auto top = q.top(); q.pop();
int ux = top.second.first,uy = top.second.second;
if (vis[ux][uy]) continue;
vis[ux][uy] = true;
for (auto V : mp[ux][uy]) {
int vx = V.first.first,vy = V.first.second,w = V.second;
if (dis[vx][vy] > dis[ux][uy] + w) {
dis[vx][vy] = dis[ux][uy] + w;
if (!vis[vx][vy]) q.push(mk(dis[vx][vy],mk(vx,vy)));
}
}
}
}
int main() {
scanf("%d%d",&n,&m);
for (int i = 1;i <= n;i ++) {
getchar();
for (int j = 1;j <= m;j ++)
mg[i][j] = getchar(),
yt[i][j] = getnum(i,j);
}
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= m;j ++) {
if (yt[i][j] == -1) continue;
if (i - 1 > 0)
addEdge(i,j,i - 1,j,turn(yt[i][j],0));
if (i + 1 <= n)
addEdge(i,j,i + 1,j,turn(yt[i][j],2));
if (j - 1 > 0)
addEdge(i,j,i,j - 1,turn(yt[i][j],3));
if (j + 1 <= m)
addEdge(i,j,i,j + 1,turn(yt[i][j],1));
}
Dijkstra();
if (dis[n][m] == 0x3f3f3f3f) dis[n][m] = -1;
printf("%d",dis[n][m]);
return 0;
}
难题
对于一条边 u → v u\to v u→v(前提是得有最短路经过它),则经过这条边的最短路条数就是:以 u u u 为终点的最短路条数 × \times × 以 v v v 为起点的最短路条数。
先判断被最短路经过的边有哪些。Dijkstra 或 SPFA 的松弛操作长这样:
min ( d i s v , d i s u + w ( u → v ) ) → d i s v \min(dis_v,dis_u+w(u\to v))\to dis_v min(disv,disu+w(u→v))→disv
显然在这两种算法结束后,对于一条边 u → v u\to v u→v,如果 d i s v = d i s u + w ( u → v ) dis_v=dis_u+w(u\to v) disv=disu+w(u→v),则说明 v v v 的最短路经过了 u → v u\to v u→v 这条边(或者边权与之相等的边),即 u → v u\to v u→v 被至少一条最短路包含。
如果我们钦定一个源点 S S S,跑最短路后把这几条被最短路经过的边单独拎出来建个图,可以发现这是张 DAG(显然最短路不会走回头路)。
还有一个性质:对于一条最短路 P P P,其路径上任意两点之间的最短路,就是 P P P 上以这两点为起点和终点的路径。
然后就可以在新建的由最短路径组成的图上拓扑排序+动态规划了。设 f i , g i f_i,g_i fi,gi 分别表示以 i i i 为终点、起点的最短路条数。显然 f S = 1 f_S=1 fS=1。转移过程中,设从 u u u 向 v v v 转移, f u + f v → f v f_u+f_v\to f_v fu+fv→fv 即可。 g g g 可以按照计算 f f f 时的拓扑序反着统计。初始时 g i = 1 g_i=1 gi=1,转移时对于一条边 u → v u\to v u→v, g u + g v → g u g_u+g_v\to g_u gu+gv→gu 即可。
最终对于一条边 u → v u\to v u→v,其答案即为 f u × g v f_u \times g_v fu×gv。
#include<bits/stdc++.h>
using namespace std;
const int maxn = 1505,maxm = 5005,P = 1e9 + 7;
int n,m,cnt,head[maxn],dis[maxn],d[maxn];
bool vis[maxn],is[maxm]; int ans[maxm];
int ans1[maxn],ans2[maxn],topq[maxn],tot;
struct edge {
int nxt,w,u,v;
} e[maxm];
void addEdge(int u,int v,int w) {
e[++ cnt] = edge{head[u],w,u,v};
head[u] = cnt;
}
void spfa(int st) {
memset(dis,0x3f,sizeof(dis));
memset(is,0,sizeof(is));
queue<int> q; q.push(st); dis[st] = 0;
while (!q.empty()) {
int u = q.front(); q.pop(); vis[u] = false;
for (int i = head[u];i;i = e[i].nxt) {
int v = e[i].v, w = e[i].w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
if (!vis[v]) {
vis[v] = true;
q.push(v);
}
}
}
}
for (int i = 1;i <= m;i ++) {
int u = e[i].u, v = e[i].v, w = e[i].w;
if (dis[v] == dis[u] + w) is[i] = true;
// cout << is[i] << ' ';
}
// putchar('\n');
}
void topo(int st) {
memset(d,0,sizeof(d));
memset(ans1,0,sizeof(ans1));
memset(ans2,0,sizeof(ans2));
queue<int> q; ans1[st] = 1; tot = 0;
for (int i = 1;i <= m;i ++)
if (is[i]) d[e[i].v] ++;
q.push(st); // st为起点,入度一定为0,其他点入读一定不为0(不是起点)
while (!q.empty()) {
int u = q.front(); q.pop(); topq[++ tot] = u;
for (int i = head[u];i;i = e[i].nxt) {
int v = e[i].v;
if (!is[i]) continue;
ans1[v] = (ans1[v] + ans1[u]) % P;
if (--d[v] == 0) q.push(v);
}
}
for (int j = tot;j > 0;j --) {
int u = topq[j]; ans2[u] ++;
for (int i = head[u];i;i = e[i].nxt) {
int v = e[i].v;
if (!is[i]) continue;
ans2[u] = (ans2[u] + ans2[v]) % P;
}
}
}
int main() {
scanf("%d%d",&n,&m);
for (int i = 1,u,v,w;i <= m;i ++) {
scanf("%d%d%d",&u,&v,&w);
addEdge(u,v,w);
}
for (int st = 1;st <= n;st ++) {
spfa(st); topo(st);
for (int i = 1;i <= m;i ++) {
if (is[i])
ans[i] = (ans[i] + (1ll * ans1[e[i].u] * ans2[e[i].v]) % P) % P;
}
}
for (int i = 1;i <= m;i ++)
printf("%d\n",ans[i]);
return 0;
}
暴力建边边数复杂度是 O ( n 3 ) O(n^3) O(n3) 的(每个点,向整个地图连边)。发现题目中多是一个点向好几个大的行进行连边。所以考虑使用线段树优化建边。
什么是优化建边?就是把原本连的边,在不影响最终答案(比如说拓扑排序时不影响连通性,求最短路时不会出现原图中不存在的最短路长度)的情况下,尽可能减少连边数量或降低连边复杂度。
线段树优化建边,通常用于处理点向区间、区间向点的连边(区间和区间连边情况更加复杂)。具体地,把线段树上的父亲与儿子之间连边权为 0 0 0 的边(方向视情况而定),对于把 [ l , r ] [l,r] [l,r] 区间向 u u u 点连边的操作,把 [ l , r ] [l,r] [l,r] 拆成线段树上的若干个节点,然后让这些节点与 u u u 之间连边。这样可以把每次建边的复杂度从 O ( n ) O(n) O(n) 降到 O ( log n ) O(\log n) O(logn),操作类似于区间加操作。
对于这一题,我们将每一行都建上一棵线段树(最终为一个森林);建完边后以这三个人分别为起点跑最短路,最后比对一下谁最优即可。具体实现看代码。
#include<bits/stdc++.h>
#define int long long
#define mk make_pair
using namespace std;
const int maxn = 305,maxm = 1e6 + 5,maxM = 2e7 + 5;
int c[maxn][maxn],r[maxn][maxn],n,m;
pair<int,int> ans[maxn]; int p[maxn];
int lson[maxm],rson[maxm],scnt,pos[maxn][maxn],nowl,nowr,st[maxn];
int dis[maxm],Ans[4][4];
struct Edge{ int v,w,nxt; } e[maxM];
int head[maxm],cnt;
void addEdge(int u,int v,int w) {
e[++ cnt] = Edge{v,w,head[u]};
head[u] = cnt;
}
int build(int x,int l,int r,int rt) {
if (l == r) {
pos[x][l] = rt;
return rt;
}
int mid = (l + r) >> 1ll;
lson[rt] = build(x,l,mid,++ scnt);
rson[rt] = build(x,mid + 1,r,++ scnt);
addEdge(rt,lson[rt],0ll);
addEdge(rt,rson[rt],0ll);
return rt;
}
void modify(int u,int l,int r,int rt,int k) {
if (nowl <= l && r <= nowr) {
addEdge(u,rt,k);
return ;
}
int mid = (l + r) >> 1ll;
if (nowl <= mid) modify(u,l,mid,lson[rt],k);
if (mid < nowr) modify(u,mid + 1,r,rson[rt],k);
}
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >q;
void Dijkstra(int s,int id) {
for (int i = 1;i <= scnt;i ++) dis[i] = 1e18;
dis[s] = 0; q.push({0,s});
while (!q.empty()) {
int u = q.top().second, length = q.top().first; q.pop();
if (dis[u] != length) continue;
for (int i = head[u];i;i = e[i].nxt) {
int v = e[i].v, w = e[i].w;
if (dis[v] > dis[u] + w) {
dis[v] = dis[u] + w;
q.push({dis[v],v});
}
}
}
for (int i = 1;i < 4;i ++) Ans[id][i] = dis[p[i]];
}
signed main() {
scanf("%lld%lld",&n,&m);
for (int i = 1;i <= n;i ++)
st[i] = build(i,1,m,++ scnt);
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= m;j ++)
scanf("%lld",&r[i][j]);
for (int i = 1;i <= n;i ++)
for (int j = 1;j <= m;j ++) {
scanf("%lld",&c[i][j]);
for (int k = max(i - r[i][j],1ll);k <= min(i + r[i][j],n);k ++) {
nowl = max(1ll,j - (r[i][j] - abs(k - i)));
nowr = min(m,j + (r[i][j] - abs(k - i)));
modify(pos[i][j],1,m,st[k],c[i][j]);
}
}
int x,y;
for (int i = 1;i < 4;i ++) {
scanf("%lld%lld",&x,&y);
p[i] = pos[x][y];
}
for (int i = 1;i < 4;i ++) {
Dijkstra(p[i],i);
ans[i].second = i - 1;
}
for (int i = 1;i < 4;i ++)
for (int j = 1;j < 4;j ++)
ans[i].first += Ans[j][i];
sort(ans + 1,ans + 4);
if (ans[1].first >= 1e18) puts("NO");
else printf("%c\n%lld",'X' + ans[1].second,ans[1].first);
return 0;
}