如何精确计算 π ?
01
原本是要回顾一下第六章内容,也就是“间隔性重复”。但我已经迫不及待,想要知道如何精确计算 π ,因此,我们快走一步,来探讨一下 π 的计算。
对于 π 的计算,我从学校时学到之后,就一直有一个疑问,说计算机可以把 π 计算到小数点后 10 亿位,100 亿位,到底是怎么计算的?
肯定不是用祖冲之或刘徽的那种算法。
我的意思是说,肯定不可能是用物理测量的方法,而一定是有一个数学的精确公式。
当然,这里所说的精确,是指一种确定性,而不是真正的某个数。现在我们已经具备了所有的条件,就看怎么来设计这个计算公式了。
02
当然, π 既然与圆周长及圆面积相关,我们还是应该从这两个概念入手。
首先,我们知道,半径为 r 的圆面积是
A(r) = πr2
因此,如果圆的半径为 1 ,那么面积则为 π 。
而我们可以将圆视为一条封闭的弯曲线条,曲线的面积计算,我们在前面已经探讨了,这里我们看是否能用上,以及如何运用。
其次,我们又探讨了曲线长度的计算,与此相对应,是圆周长的计算,而我们知道半径为 r 的圆,周长是
L(r) = 2πr
同样,半径 r=1 ,那么周长为 2π 。
然后呢?
由于我们讨论的微分与积分,均与函数相关,我们于是可以将 A(r) 与 L(r) 都看成是函数。又因为当 r = 1 时,就可以得到纯粹的 π ,那么,我们可以将这两个函数看成是 A(1) 与 L(1) 。即
A(1) = π
L(1) = 2π
然后呢?
好像毫无头绪。
老办法,我们再回过头去看看走过的老路,看能不能绕到老路上去。
03
如果有一种函数,当 x=1 时,m(x)= π 呢?
当然会有,比如
m(x)= πx
或者
m(x)= πx
这两种函数在 x=1 时,m(x)= π 。
但我们知道, m(x)= πx 其实是以 π 为斜率的直线,显然不是。
m(x)= πx
是不是呢?
也不好说。
这是一个指数函数,我们前面讨论过,我们还知道指数函数有一个特殊的数 e , f(x)=ex ,其导数就是其本身,即
(ex)'=ex
而且,我们还通过泰勒级数,计算出了 e 大约等于 2.71828。
那么,我们可不可以利用泰勒级数,像计算 e 一样,计算出 π 呢?
可以试试。
04
使用泰勒级数之前,从哪里开始呢?
我们应该想到,曲线的面积与长度,均与积分相关,而积分,又与反导数相关。
那么,我们在考察 A(1) 与 L(1) 函数,输入 1 ,输出 π 的同时,是不是应该思考有没有什么函数,输入 π 而输出 1 呢?
有的。或者说,有相似的函数。
那就是正弦函数 f(x)=sin(x) 。
我们前面在探讨正弦函数的时候,其实是以半径为 1 的圆来考察的,这与我们本篇文章的设定恰好完全一致。
我们也知道了,如果以圆周长来定义角度,那么
sin(π/2)=1
即输入 π/2,输出 1 。符合我们的设想。
也就是说,现在我们想要有两种函数,一种函数是输入 1 ,输出 π ;一种函数是输入 π ,输出 1 。我们设前一种函数为 ∧ ,后一种函数为 ∨ ,没有别的意思,仅仅是因为 ∧ 与 ∨ 这两个符号看起来相反。我们命名为 qp ,或者 db 也行。
那么,我们希望得到的两种函数,二者关系如下:
∧(∨(x))=x
或者
∨(∧(x))=x
我们让 ∨(x) 就是 sin(x) ,即
∨(π/2)=1
那么
∧(1)=π/2
即
π= 2·∧(1)
我们再让 A(x)= ∧(∨(x)) ,其实也就是 A(x)=x 。
很显然,A(x)= x 是斜率为 1 的直线,即
A'(x)=dA/dx
=1
把 A(x)= ∧(∨(x)) 代入,即
1= dA(x)/dx
= d∧(∨(x))/dx
= [d∧(∨(x))/d∨]·[d∨/dx]
这是什么东西啊?
完全没有头绪啊。
不过,前面我们已经令 ∨(x) = sin(x) ,而我们也在三角函数的导数(数学学习 030)中,知道 sin(x) 的导数为 cos(x) 。即
d∨/dx = cos(x)
我们设 H(x)= cos(x) 吧,那么
1=H(x)·[d∧(∨(x))/d∨]
好像也没有什么头绪,我们还有 d∧(∨(x))/d∨不知道是什么东西。
怎么办呢?
05
我们还是从 d∧(∨(x))/d∨入手。
[d∧(∨(x))/d∨] 似乎可以简写为
d∧(∨)/d∨
内涵没变,只是看起来简单一点,即
1=H(x)·[d∧(∨)/d∨] (1)
变一下形
d∧(∨)/d∨=1/H(x)
这里的 H(x) 显得很突兀,我们还是把 H(x) 改为用 ∨(x) 来表示吧。
怎么改呢?
我们知道,根据毕达哥拉斯定理
[sin(x)]2+[cos(x)]2=1
那么
cos(x)=[1-(sin(x))2]1/2
即
d∧(∨)/d∨=1/[1-∨2]1/2
我们令 ∨=x ,那么

不过,经过几次的变换之后,这个公式当中的 x ,还是那个变量吗?会不会变成了一个“约束变量”?
我们可以检验一下。
06
所谓检验,可以是我们试着用另外一种途径来运算,看会不会得出同样的结果。
前面,我们的出发点是 A(x)= ∧(∨(x)) ,即 A(x)=x ,即 A(x) 的导数为 1 。那么,我们这次的出发点改为 A(x)= ∨(∧(x)) ,还是 A(x)=x ,导数为 1 。
1=[dA(x)]/dx
因为 A(x)= ∨(∧(x)) ,即
1=[d∨(∧(x))]/dx
= [d∨(∧(x))]/dx·[d∧(x)/d∧(x)]
= [d∧(x)/dx]·[d∨(∧(x))]/d∧(x)
简化一下,即
1=[d∧/dx]·[d∨(∧)]/d∧
其中
[d∨(∧)]/d∧,其实就是前面说过的 H(∧),即
1=[d∧/dx]·H(∧)
同样,我们用 ∨(∧) 来表示 H(∧) 。即
H(∧)=[1-(∨(∧))2]1/2
那么
1=[d∧/dx]·[1-(∨(∧))2]1/2
变形
d∧/dx= 1/[1-(∨(∧))2]1/2
而
∨(∧)=∨(∧(x))
= x
即
d∧/dx= 1/[1-x2]1/2
即

Perfect 。
07
不过,我们做到现在,似乎越走越远了,都忘了一开始我们是为了什么出发。
我们回头看看,这个 ∧是什么?
哦,原来是圆的面积函数 A(x) ,其中 x 就是圆的半径。而且,我们也知道了,如果圆的半径为 1 ,那么
A(1)=π
不过,为了与 V(x) 统一,我们最后计算出 π=2 ∧(1) 。
既然 ∧(x) 就是圆的面积函数,那么对其求导之后的 d∧/dx 不就是相当于积分中的 m(x) 吗?也就是
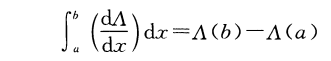
我们可以让 b=1 ,不就是 ∧(1) 吗?而且,我们也可以把 d∧/dx= 1/[1-x2]1/2 代入这个公式,即

嗯, ∧(1) 有了,后面这个 ∧(a) 有点讨嫌,能够去掉吗?
我们让 a=0 试试。
因为 V(x)=sin(x),所以 V(0)=0 ,而 A(V(0))=0 即 A(0)=0 。那么

啊哈,我们将 π=2 ∧(1) 代进去,π 的表达式就是

这个根号好像有一点讨嫌,能不能去掉呢?
08
我们记得三角函数中,正切的导数有一个 T2 ,没有根号。我们将 Tan(x) 简化为 T(x) ,即
T'(x)=1+T2
能不能用 tan 解决上述根号问题呢?
首先用 sin(x) 即 V(x) 和 cos(x) 即 H(x) 来表示 T(x) ,即
T(x)= V(x)/H(x)
我们知道,当 x = π/4 时,V=H ,即
T(π/4)= 1
我们设 ⊥(x) 是 T(x) 的反函数,也就是
⊥(T(x))=x
或
T(⊥(x))=x
因为T(π/4)= 1,那么
⊥(1)=⊥(T(π/4))
=π/4
变形
π= 4 ·⊥(1)
我们之前已经假设了 A(x)=x ,而⊥(T(x))=x ,因此
A(x)=⊥(T(x))
求导
1= dA/dx
= d⊥(T(x))/dx
= d⊥(T(x))/dx·dT(x)/dT(x)
=[dT/dx]·[d⊥(T)]/dT
而 dT/dx = 1+ T2
代入
d⊥(T)/dT=1/(1+ T2)
由于全部是 T ,因此 T 可以用 x 表示,即
d⊥(x)/dx=1/(1+ x2)
同样,求积分

令 a=0 ,b=1 ,结合 π= 4 ·⊥(1) 我们可以得到 π 的表达式

嗯,这感觉好一点。
现在可不可以使用泰勒级数了呢?
我们试试,为了简化,我们可以先令 s=x2 ,即令
m(s)=(1+s)-1
那么
m'(s)=(-1)·(1+s)-2
m''(s)=(-1)·(-2)·(1+s)-3
……
m(n)(s)=(-1)·(-2)·…·(-n)(1+s)-n-1
即
m(n)(0)=(-1)·(-2)·…·(-n)
=(-1)n·n!
好,现在开始用泰勒级数,即

将 s 换回 x2 ,即

代入 π 的表达式

新的 π 的表达式为
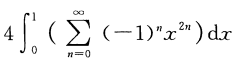
好像有点麻烦,好复杂,换一种形式

我们再利用积分公式
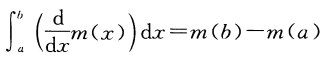
将 π 的表达式改为

即

其实也可以表述为

09
这就好办了,我们交给计算机来计算。
当 n=100,000 时
π =3.141 60
当 n=1,000,000 时
π=3.141 59
因此,我们可以根据计算机的计算能力,不断地扩大 π 小数点后的位数。
随着科技的不断进步和发展,截止到2021年8月17日,瑞士的研究人员使用了一台超级计算机,经历了108天,精准地将圆周率 π 计算到了小数点后的62.8万亿位。