机器学习知识点复习中（保研、复试、面试）百面机器学习笔记

机器学习知识点复习中

第五章、非监督学习
- 1.K均值聚类 k-means
- 2.高斯混合模型GMM
第六章、概率图模型
- 1.贝叶斯
- 2.马尔科夫
第七章、优化算法

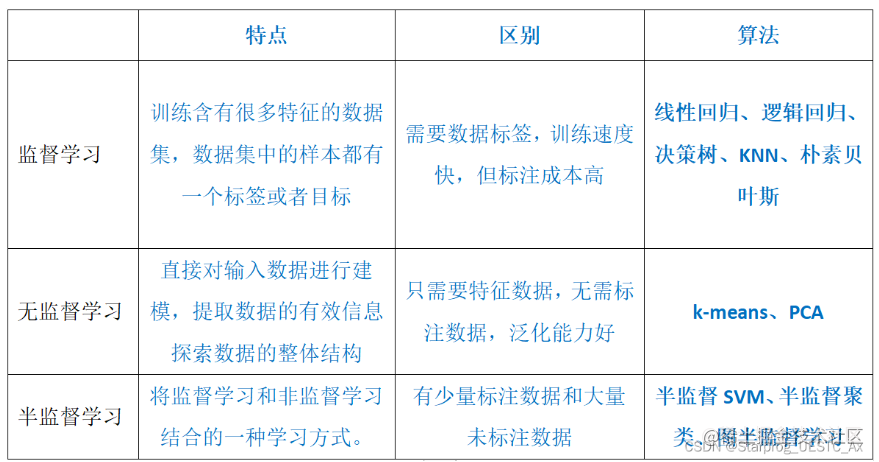
第五章、非监督学习

1.K均值聚类 k-means

通过迭代方式寻找K哥簇的一种划分方案，使得聚类结果对应的代价函数最小。其中，损失函数可以定义为各个样本距离所属簇中心点的误差平方和：
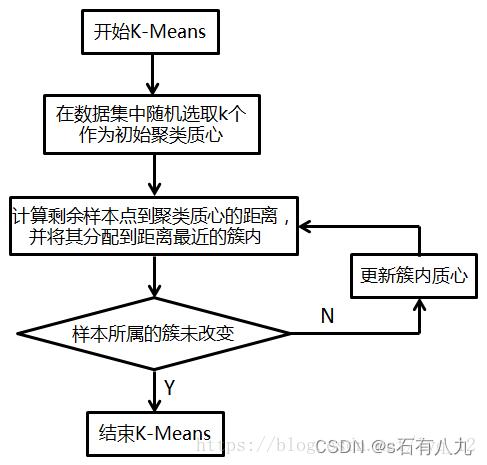
在这里插入图片描述

K-Means步骤及流程
输入：样本集D，簇的数目k，最大迭代次数N；
输出：簇划分（k个簇，使平方误差最小）；
算法步骤：
（1）为每个聚类选择一个初始聚类中心；
（2）将样本集按照最小距离原则分配到最邻近聚类；
（3）使用每个聚类的样本均值更新聚类中心；
（4）重复步骤（2）、（3），直到聚类中心不再发生变化；
（5）输出最终的聚类中心和k个簇划分

这里步骤引用的一个博主的，写的很好，原文链接：https://blog.csdn.net/lyq_12/article/details/81043690
问题：K-means的优缺点是什么？如何对其进行调参？

2.1 优点：

原理易懂、易于实现；
高效可伸缩，计算复杂度O(NKt)为接近于线性（N是数据量，K是聚类总数，t是迭代轮数）;
当簇间的区别较明显时，聚类效果较好。

2.2 缺点：

受初始值和异常点影响，聚类结果可能不是全局最优而是局部最优
k的取值十分关键，对不同数据集，k选择没有参考性，需要大量实验；
当样本集规模大时，收敛速度会变慢。

2.3 调优：

数据归一化和离群点处理。
合理选择K值。手肘法认为拐点就是K的最佳值，更先进的有Gap Statistic 方法。
采用核函数。核聚类方法的主要思想：是通过一个非线性映射，将输入空间中的数据点映射到高位的特征空间中，并在新的特征空间中进行聚类。。非线性映射增加了数据点线性可分的概率。

针对K均值的缺点，有哪些改进的模型？
主要缺点：
（1）需要入工预先确定初始K值，且该值和真实的数据分布未必吻合。
（2）K均值只能收敛到局部最优，效果受初始值影响大。
（3）易受到噪声影响。
（4）样本点只能被划分到单一的类中。
K-means++ 算法
原始K均值算法最开始随机选取数据集中K个点作为聚类中心，K-means++按照如下的思想选取K个聚类中心：假设已经选取了n个初始聚类中心( O<n<K ），则在选取第 n+1 个聚类中心肘，距离当前n个聚类中心越远的点会有更高的概率被选为第 n+1 个聚类中心。
ISODATA 算法
一分裂操作： 当属于某个类别的样本数过少时，把该类别去除；
二合并操作： 当属于某个类别的样本数过多、分散程度较大时，把该类别分为两个子类别。

2.高斯混合模型GMM

高斯混合模型与K均值算法的相同点是，它们都是可用于聚类的算法，都需要指定K值；都是使用EM算法来求解;都往往只能收敛于局部最优。
而它相比于K均值算法的优点是，可以给出一个样本属于某类的概率是多少；不仅仅可以用于聚类，还可以用于概率密度的估计;并且可以用于生成新的样本点。
通俗的理解：
当数据的分布（肉眼）是圆形，这很还凑合用。但是，当数据呈现不同的形状时，最终会得到如下图的结果，似乎很难符合人类的分类认知；
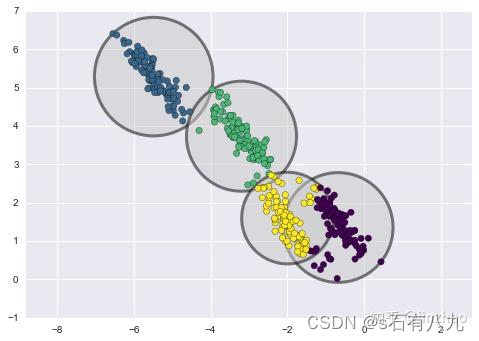
在这里插入图片描述
相反，高斯混合模型（Gaussian Mixture Models）很擅长这方面甚至可以处理非常长的簇。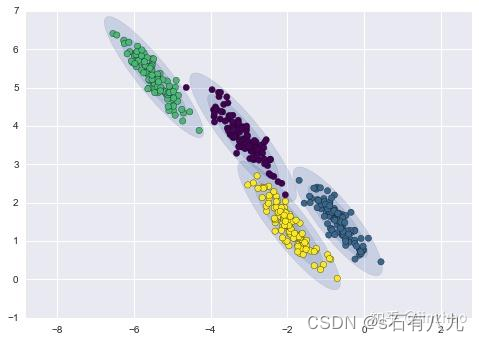
通俗的理解引用自https://zhuanlan.zhihu.com/p/151671154

第六章、概率图模型

1.贝叶斯

一种典型的生成式模型，属于有监督学习

2.马尔科夫

第七章、优化算法

机器学习算法 = 模型表征 + 模型评估 + 优化算法

1.问题：有监督学习涉及的损失函数有哪些？请列举并简述它们的特点。

0-1损失函数：用于二分类问题，当预测值和真实值相同时，损失为0，否则为1。它直接反映了分类的错误率，但是非凸、非光滑，难以优化。
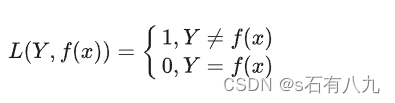
Hinge损失函数：用于支持向量机（SVM）算法，当预测值和真实值的乘积大于等于1时，损失为0，否则为1减去乘积。它是0-1损失函数的凸上界，且当预测值和真实值一致时，不做惩罚。它在某些点不可导，需要用次梯度下降法优化。
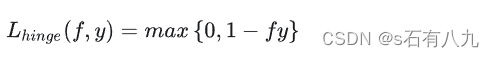
Logistic损失函数：用于逻辑回归算法，当预测值和真实值的乘积越大时，损失越小，趋近于0，当乘积越小时，损失越大，趋近于无穷。它是0-1损失函数的光滑凸上界，且处处可导，可以用梯度下降法优化。但是，它对所有的样本都有惩罚，对异常值敏感。
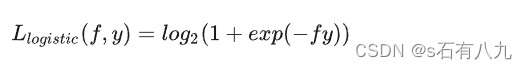
交叉熵损失函数：用于多分类问题，当预测值和真实值越接近时，损失越小，趋近于0，当预测值和真实值越远时，损失越大，趋近于无穷。它是0-1损失函数的光滑凸上界，且处处可导，可以用梯度下降法优化。它可以衡量两个概率分布的相似性，常用于神经网络中。

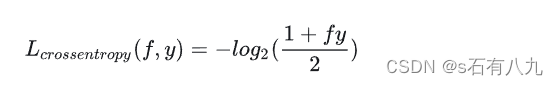
上面四个损失函数的曲线如下：
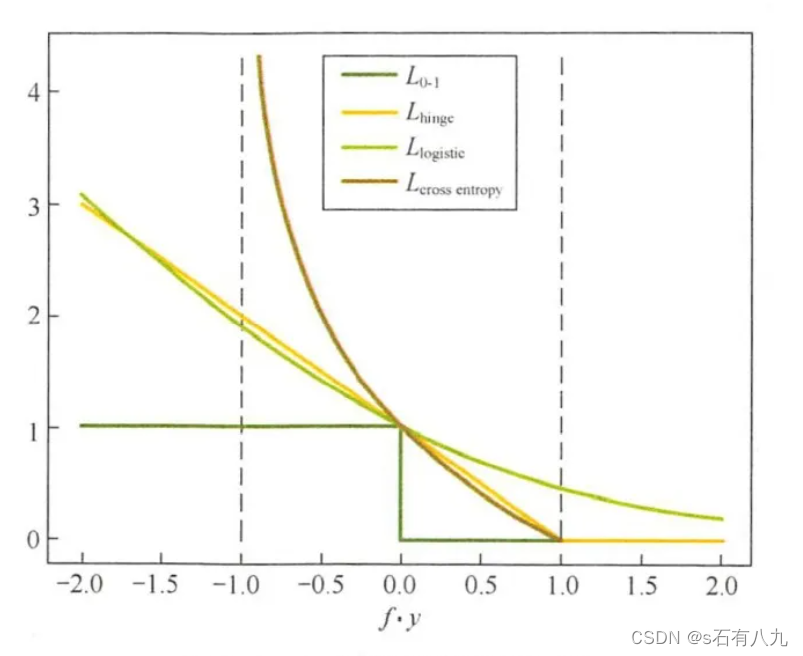
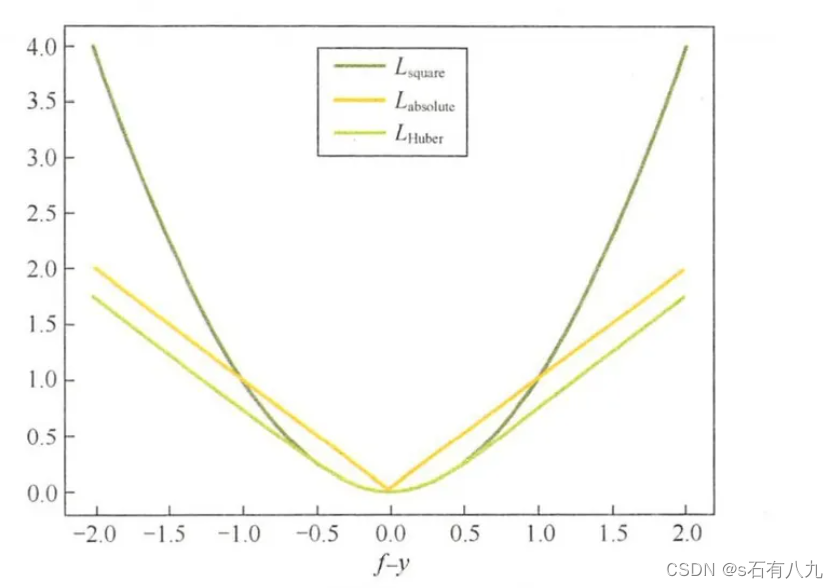
平方损失函数：用于回归问题，当预测值和真实值的差值越小时，损失越小，当差值越大时，损失越大。它是光滑函数，可以用梯度下降法优化。但是，它对异常值敏感，容易受到噪声的影响。
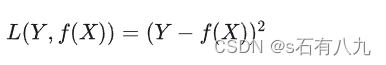
绝对损失函数：用于回归问题，当预测值和真实值的绝对差值越小时，损失越小，当绝对差值越大时，损失越大。它相比平方损失函数，对异常值更鲁棒，但是在某些点不可导，需要用次梯度下降法优化。
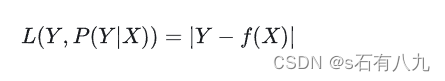
Huber损失函数：用于回归问题，当预测值和真实值的绝对差值小于某个阈值时，损失为平方损失，否则为线性损失。它综合了平方损失函数和绝对损失函数的优点，既光滑又鲁棒，可以用梯度下降法优化。

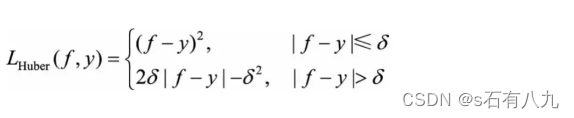
上面三种损失函数曲线如下：

2.梯度下降法

问题：当训练数据量特别大时，经典的梯度下降法存在什么问题，需要做如何改进?
（1）存在的问题：经典的梯度下降法采用所有的训练数据的平均损失近似目标函数。每次更新模型参数，需要遍历所有的训练数据。当数据量比较大时，计算量大，耗时长。
（2）为解决上述问题，随机梯度下降法SGD用单个训练样本的损失来近似平均损失，也就是说使用单个数据即可对模型进行一次更新，加快了收敛速率。适合于数据源源不断到来的在线更新场景。
（3）为降低随机梯度的方差，从而使得迭代算法更加稳定，也为了充分利用高度化的矩阵运算操作，在实际应用中我们会同时处理若干个训练数据，该方法被称为小批量梯度下降法。
小批量梯度下降法的使用： 假设处理n个训练数据，
（1）n的选择通过调参选择最合适的。n可选择的一般为2的幂次，32、64，128、256等。
（2）挑选 n个训练数据，先遍历，再随机。为了避免数据的特定顺序给算法收敛带来的影响，一般会在每次遍历训练数据之前，先对所有的数据进行随机排序，然后在每次迭代时按顺序挑选m个训练数据直至遍历完所有数据。
（3）选取学习率α，先大再小。通常采用衰减学习速率的方案：一开始算法采用较大的学习速率，加快代价函数收敛速度，当误差曲线进入平稳期后，减小学习速率做更精细的调整。但最优的学习速率也需要调参。

3.随机梯度下降法SGD

问题：随机梯度下降法失效的原因–摸着石头下山
批量梯度下降法BGD训练集都载入，睁着眼睛下山，正确性高但是开销大。
随机梯度下降法SGD只随机采样一步，闭着眼睛下山，开销小但是偏差大。
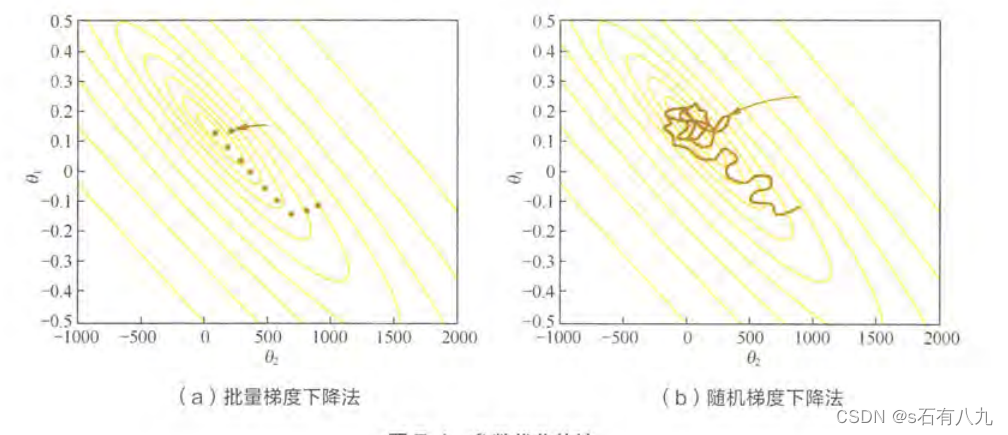
问题：解决梯度下降法失效–惯性保持和环境感知
（1）动量方法：可以直观理解成一个小球沿着山道下降，由于惯性减弱山壁间来回震荡并突破鞍点。惯性就体现在对前一次更新信息的重利用上。衰减系数扮演了阻力的作用。与随机梯度下降法相比，动量方法的收敛速度更快，收敛曲线也更稳定。
（2）AdaGrad方法：
AdaGrad方法梯度下降法是一种自适应的优化算法，它可以根据每个参数的历史梯度来调整学习率，使得不同参数有不同的更新速度。AdaGrad的主要思想是：
①对于出现频率高的参数，它们的梯度累积会很大，因此AdaGrad会降低它们的学习率，避免过度更新。
②对于出现频率低的参数，它们的梯度累积会很小，因此AdaGrad会增加它们的学习率，加速更新。
（3）Adam方法：该方法将惯性保持和环境感知这两个优点集于一身。一方面，Adam记录梯度的一阶矩，即过往梯度与当前梯度的平均，这体现了惯性保持；另一方面，Adam还记录了梯度的二阶矩，即过往梯度平方与当前梯度平方的平均，这类似AdaGrad方法中的环境感知能力，为不同参数产生自适应的学习率。

3.L1正则化与稀疏性

为什么希望模型具有稀疏性？
稀疏性就是一些特征的参数为0，稀疏性可以实现模型的特征选择，只保留一些重要的特征，去除一些冗余或无关的特征。
L1正则化使得模型参数具有稀疏性的原理是什么？（详解可看课本P164）
（1）从解空间形状角度理解：如果原问题目标函数的最优解不是恰好落在解空间内，那么约束条件下的最优解一定是在解空间的边界上，L2正则化项约束后的解空间是圆形，而L1正则化项约束的解空间是多边形。显然，多边形的解空间更容易在尖角处与等高线碰撞出稀疏解。（“带正则项”和“带约束条件”是等价的，都是为了约束w的可能取值空间从而防止过拟合）。
（2）从函数叠加角度理解：加入L1正则化后，对带正则项的目标函数求导，正则项部分产生的导数在左边部分是-C，在原点右边部分是C，因此只要目标函数的倒数绝对值小于C，那么带正则项的目标函数在原点左边部分始终是递减的，在原点右边部分始终是递增的，最小值点自然是原点处，此时对应的w为0，产生了稀疏性。相反，L2正则项在原点处的导数是0，只要原目标函数在原点处的导数不为0，那么最小值点就不会在原点，所以L2只有减小w绝对值的作用，对解空间的稀疏性没有贡献。
（3）在一些在线梯度下降算法中，往往会采用截断梯度法来产生稀疏性，这同L1正则项产生稀疏性的原理类似