数据结构-Treap
前置知识
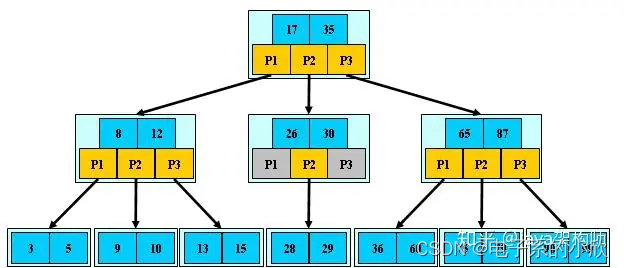
- 平衡树
- 二叉堆
思路
Treap 是平衡树的一种。
Treap=tree+heap=树堆 确实是这样的。
Treap 的每个节点维护两个值,原本的点权和随机生成的权重。Treap 对于点权满足 BST 的性质,对权重满足堆的性质,就可以达到 O ( log n ) O(\log n) O(logn) 的期望复杂度了。
下面来讲一下 Treap 各主要函数的实现。
Insert \text{Insert} Insert
插入节点。
先根据 BST 的性质插入元素为叶子节点,然后从叶子节点回溯至根节点,对不符合堆的性质的失衡子树做相应的旋转。
Delete \text{Delete} Delete
删除节点。
需要将该节点逐层旋转至叶子节点,同时需要维护堆的性质,最终在叶子处删除节点。
GetRnk \text{GetRnk} GetRnk
查询值对应的排名,该函数返回的其实是比该元素小的元素的数量。
利用 BST 的性质,每次向下需要加上该节点的同权值元素数,若向右子树递归则需要再加上左子树的大小。
GetVal \text{GetVal} GetVal
查询排名对应的值。
利用 BST 的性质,每次向下时重新计算目标节点在子树中的排名,递归即可。
GetPre \text{GetPre} GetPre
查询节点的前驱,即最大的比该元素小的数。
从根节点向下,若节点比该元素权值小,就向右子树递推,否则向左子树递推即可。
GetNxt \text{GetNxt} GetNxt
查询节点的后继,即最小的比该节点大的数。
从根节点向下,若节点比该元素权值大,就向左子树递推,否则向右子树递推即可。
数据结构参数
- 单次修改时间复杂度: Θ ( log n ) \Theta(\log n) Θ(logn)
- 单次查询时间复杂度: Θ ( log n ) \Theta(\log n) Θ(logn)
- 空间复杂度: Θ ( n ) \Theta(n) Θ(n)
实现代码
代码比较长。考验码力。
int root,tot;//root 根 //tot 节点数
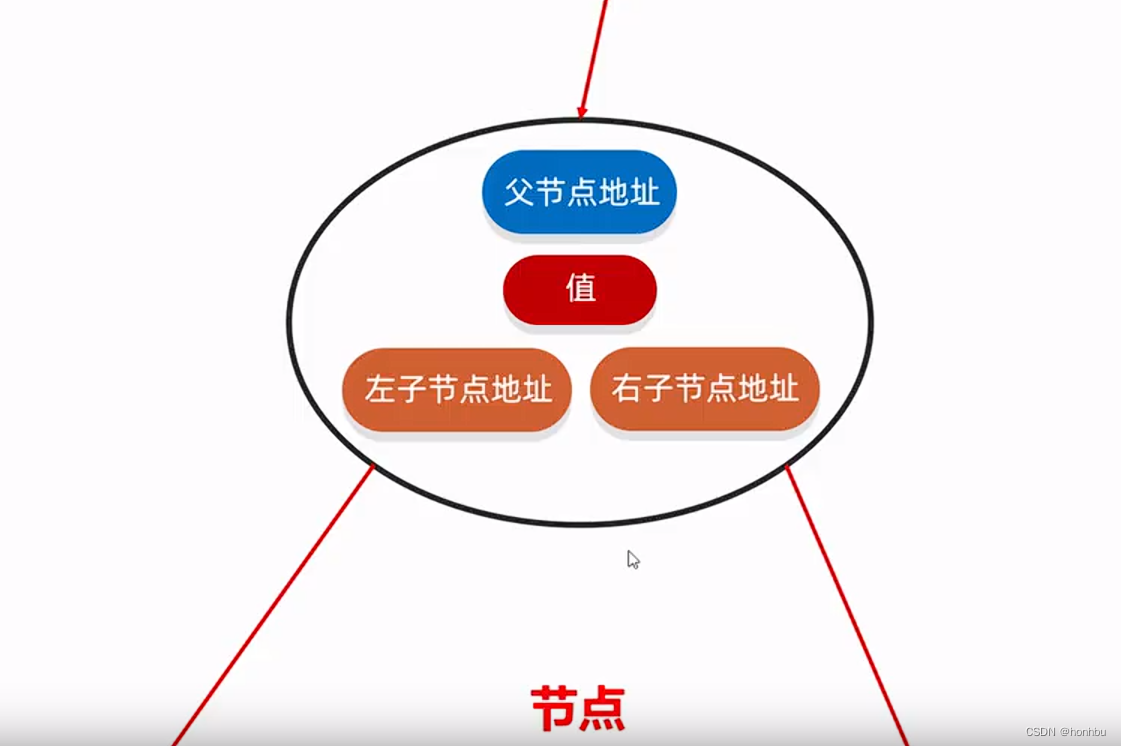
struct node{
int v,k,l,r,s,c;//v 权值 //k 随机权重 //l 左子节点 //r 右子节点 //s 子树大小 //c 同权值节点个数
}t[N];//Treap
void Pushup(int p){
//更新子树大小
t[p].s=t[t[p].l].s+t[t[p].r].s+t[p].c;
}
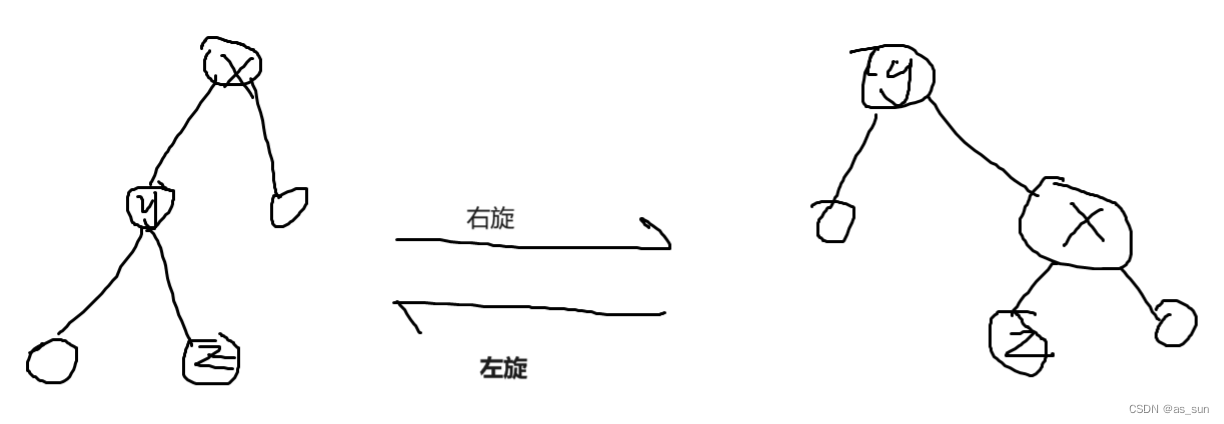
void Zag(int &p){
//左旋
int q=t[p].r;
t[p].r=t[q].l;
t[q].l=p;p=q;
Pushup(t[p].l);Pushup(p);
}
void Zig(int &p){
//右旋
int q=t[p].l;
t[p].l=t[q].r;
t[q].r=p;p=q;
Pushup(t[p].r);Pushup(p);
}
int Create(int x){
//创建节点
int k=++tot;
t[k].v=x;
t[k].s=t[k].c=1;
t[k].l=t[k].r=0;
t[k].k=rand();
return k;
}
void Insert(int &p,int x){
//插入
if (!p){
p=Create(x);return;}
if (x==t[p].v){
t[p].c++;t[p].s++;return;}
if (x<t[p].v) Insert(t[p].l,x);
if (x>t[p].v) Insert(t[p].r,x);
if (t[p].k<t[t[p].l].k) Zig(p);
if (t[p].k<t[t[p].r].k) Zag(p);
Pushup(p);
}
void Delete(int &p,int x){
//删除
if (!p) return;
if (t[p].v==x){
if (t[p].c>1){
t[p].c--;Pushup(p);return;}
if (t[p].l||t[p].r){
if (!t[p].r||t[t[p].l].k>t[t[p].r].k) Zig(p),Delete(t[p].r,x);
else Zag(p),Delete(t[p].l,x);
Pushup(p);
}
else p=0;
return;
}
if (x<t[p].v) Delete(t[p].l,x);
else Delete(t[p].r,x);
Pushup(p);
}
int GetRnk(int p,int v){
//获取排名,该函数返回的其实是比该元素小的元素的数量
if (!p) return 1;
if (v==t[p].v) return t[t[p].l].s+1;
else if (v<t[p].v) return GetRnk(t[p].l,v);
else return t[t[p].l].s+t[p].c+GetRnk(t[p].r,v);
}
int GetVal(int p,int x){
//获取权值
if (!p) return INF;
if (t[t[p].l].s>=x) return GetVal(t[p].l,x);
if (t[t[p].l].s+t[p].c>=x) return t[p].v;
return GetVal(t[p].r,x-t[t[p].l].s-t[p].c);
}
int GetPre(int x){
//获取前驱
int p=root,pre;
while (p)
if (t[p].v<x) pre=t[p].v, p=t[p].r;
else p=t[p].l;
return pre;
}
int GetNxt(int x){
//获取后继
int p=root,nxt;
while (p)
if (t[p].v>x) nxt=t[p].v, p=t[p].l;
else p=t[p].r;
return nxt;
}
void BuildT(){
//建树
Insert(root,INF);Insert(root,-INF);
Pushup(root);
if (t[root].k<t[t[root].l].k) Zig(root);
}