二叉搜索树

1 二叉搜索树

1.1 概念

我们在学习C语言数据结构的时候就说了，二叉树一般适用于一些特殊的场景或者特殊的用途，如果从单纯存储数据的角度来说，二叉树是不如vector和list等容器的。但是如果我们给二叉树加上一些规则，那么二叉树在某些场景下就很有意义了，就比如我们要讲的二叉搜索树。

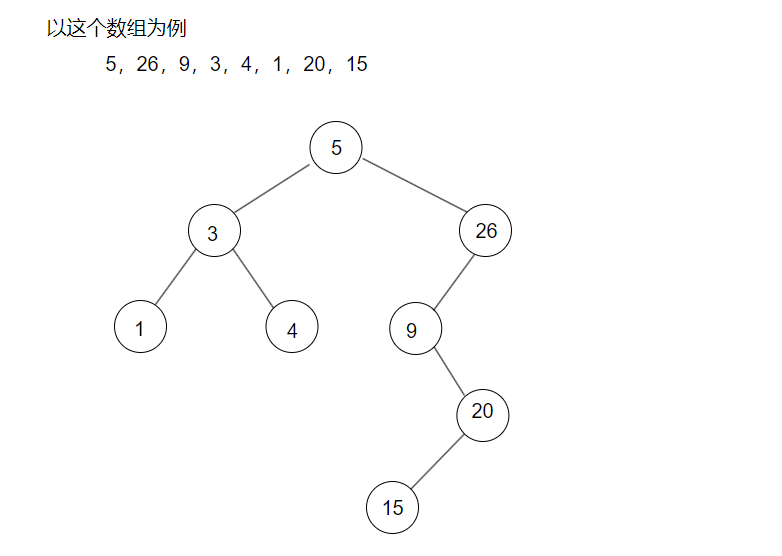
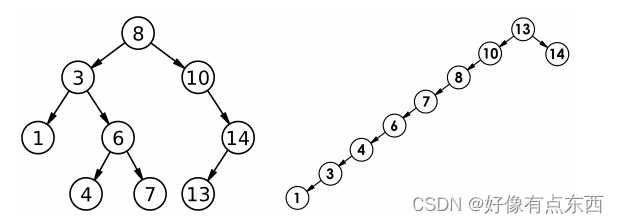
二叉搜索树有什么特点呢？拿下面的图来举例

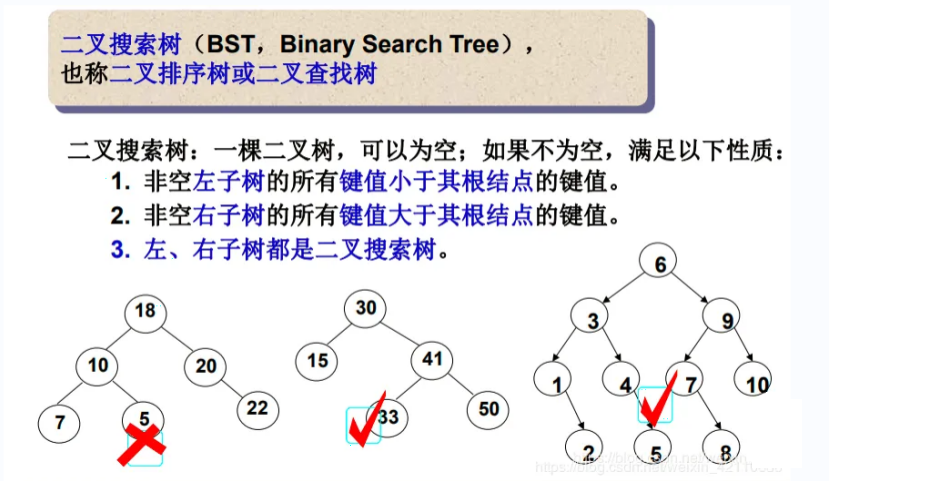
二叉搜索树（BST：Binary Search Tree）：对于任何一个节点，左子树的所有节点的值小于根，右子树的所有节点的值大于根，同时，左右子树都要满足上述条件。二叉搜索数也可以是一颗空树。

那么如此一来，对二叉搜索树走中序遍历，那么遍历访问的数据的顺序就是有序的，所以他也叫做二叉排序树。但是他的主要功能不是排序，而是搜索或者说查找某一个值，我们以前的查找都是暴力的查找，虽然我们学过二分查找，但是二分查找的前提条件太过严苛，要求数据必须是有序的同时要支持下标访问，也就是要是连续的顺序结构。但是二叉搜索树就没有这么麻烦，只要有一颗二叉搜索树，我们要在这棵树中去查找某一个值，那么我们拿这个值去跟根节点比较之后，就能排除一棵子树，只需要到其中的一棵子树去查找。我们可以想象，二叉搜索树的查找的效率最好的情况就是O(log2 N)，最好的情况发生在二叉搜索树是一颗完全二叉树或者接近完全二叉树的时候，而他的最坏情况则是 O(N)，这时候二叉搜索树接近一棵单只树或者两边高度差距很大。

1.2 模拟实现

二叉搜索树的结构和特点我们不难理解，那么我们该怎么实现一棵二叉搜索树呢？首先搜索二叉树的节点的结构还是和以前的二叉树没什么区别，无非就是多了一个模板。二叉搜索树就是在我们以前实现的二叉树的基础上加了一些规则，让他在某些场景能够发挥出它的优势。

那么节点的定义如下

template<typename K>
struct BSTNode
{
	K _key;
	BSTNode* _left;
	BSTNode* _right;

	BSTNode(K key)
		:_key(key),_left(nullptr),_right(nullptr)
	{}
};

在使用这种非线性的数据结构的时候，我们一般把数据的变量名叫做key而不再是val，把模板的参数名叫做K而不是T了，我们后面会讲K模型以及KV模型，使用K更加贴合这两种使用场景。

那么一个BSTree对象只需要保存这棵树的根节点就行了。

template<typename K>
class BSTree
{
public:
	typedef BSTNode<K> Node;
	BSTree() //默认构造
		:_root(nullptr)
	{}

private:
	Node* _root;
};

二叉搜索树的构造函数不是重点，他的重点是插入和删除这两个接口，不过在实现这两个接口之前，我们可以先实现一下查找和中序遍历，中序遍历方便我们的调试，查找则是二叉搜索树要实现的必要接口，这毕竟是二叉搜索树要达成的目标。

	void Inorder()const  //中序遍历调用的函数
	{
		Inorder(_root); //中序遍历实际进行遍历的子函数
		cout << endl;
	}

    //子函数可以设为private，因为用户反正也不能直接访问到_root，设为公有也没用，设为私有还能隐藏
	void Inorder(const Node* root)const
	{
		if (root == nullptr)
			return;

		if (root->_left)
			Inorder(root->_left);

		cout << root->_key << " ";

		if (root->_right)
			Inorder(root->_right);
	}

	//查找
	Node* find(const K& key)const
	{	
		if (!_root)
			return nullptr;
		return find(_root, key);
	}

    //查找的子函数
    Node* find(const Node* root, const K& key)const 
	{
		//每一个节点的左子树的所有节点的值都比它小，右子树的所有的节点的值都比他大
		while (root)
		{
			if (root->_key == key)
				return root;
			else if (key < root->_key)
				root = root->_left;
			else
				root = root->_right;
		}
		return false;
	}

insert，在搜索二叉树中插入数据的话，第一步就是要找到该数据要插入的位置，因为我们插入数据之后还是要保证这棵树是一棵二叉搜索树，不能违反他的的规则。

同时，插入这里还有一个问题，就是我们是否允许相同的值存在，如果允许，那么应该如何插入。在我看来，二叉搜索树毕竟是用来高效查找数据的，如果一棵树中有相同的数据可以说是一种冗余，没有必要，但是如果确实有这种需求的话，还是也可以根据自己的想法进行插入。在这里我们实现的是一颗不允许数据重复的二叉搜索树，那么我们的insert就有可能插入失败，也就是二叉树中已有该数据的时候，我们就觉得是插入失败，不创建新节点插入了。

	//插入
	bool insert(const K& key)
	{
		//判断是否为空树
		if (_root == nullptr)
		{
			Node* newnode = new Node(key);
			_root = newnode;
			return true;
		}
		//不是空树，需要找到插入的位置
		Node* parent = nullptr;//保存最终位置的父节点，用来连接新节点
		Node* cur = _root;

		while (cur)
		{
			parent = cur;
			if (cur->_key == key)
				return false;
			else if (key < cur->_key)
				cur = cur->_left;
			else
				cur = cur->_right;

		}
		//走到这里说明cur遍历到了nullptr，也就是说 parent 就是新节点的父节点
		cur = new Node(key);
		//判断一下是连接到左边还是右边
		if (key < parent->_key)
			parent->_left = cur;
		else
			parent->_right = cur;

		return true;
		
	}

插入写完之后我们可以先测试一下插入的逻辑是否有问题

void testBST1()
{
	BSTree<int> b;
	int arr[] = { 5,3,6,7,1,3,5,0,9,8 };
	for (auto e : arr)
		b.insert(e);
	b.Inorder();
}

目前来说确实将数据按照搜索树的规则放好了。

那么接下来就来实现一下删除erase

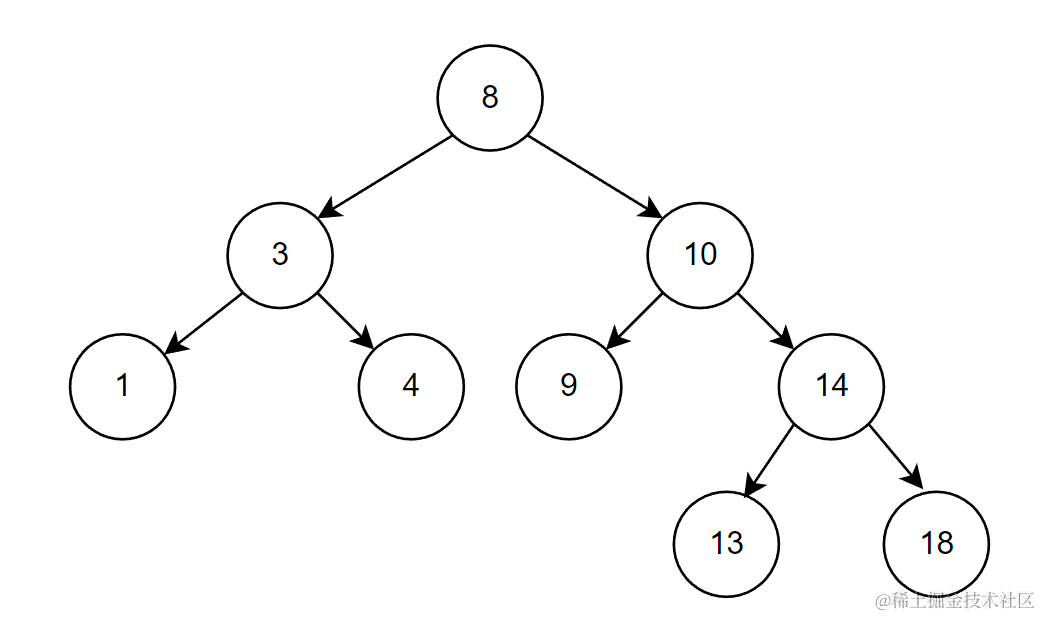
在删除的实现中我们就要考虑各种情况了，首先最简单的肯定是删除叶子节点，比如下面这种情况

删除叶子节点我们只需要释放该节点并且将他的父节点的链接关系修改为nullptr就行了。

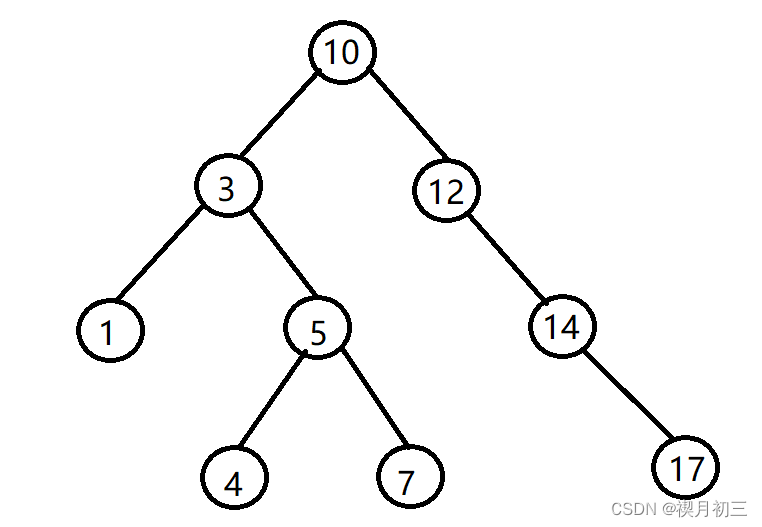
其次是删除一棵单支子树的根节点的情况

比如上面的图中，我们要删除 2 或者 9 的节点，2 和 9 这两个节点都只有一棵子树，另一边为空，这种删除也很简单，我们只需要将要删除的子节点中不为空的子树的根节点连接到它原本在父节点的位置，然后删除该节点就行了

删除的节点只有一颗子树的时候，还有另外一种情况，就是左树的右子树或者右树的左子树，也就是下图中的情况

其实这里的操作还是没有区别，不需要特殊处理，为什么呢？我们举个例子，比如上图中要删除 2 ，而2是 4 的左子树，那么意味着 2 和 3 都是比 4 小的值的，这样一来，把 3 链接到2的原来的位置也是没问题的，因为 3 本来就是 4 的左子树的节点，成为 4 的左子树没有任何问题。这里就算 3 是一颗子树也是一样的。我们可以把这种行为形象一点叫做托孤

这种情况其实可以将第一种最简单情况也一并解决了。

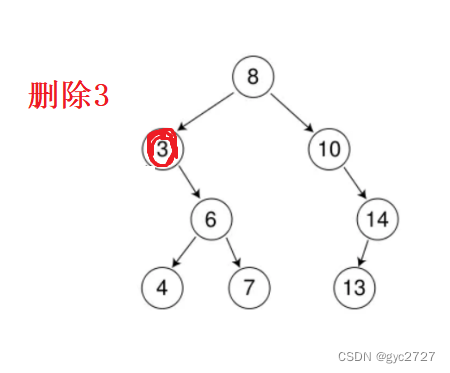
最难的一种情况就是要删除的节点的左右都不为空的时候，

如上图，这种情况该怎么办呢？这个类型地删除其实就是要删除一棵搜索二叉树的根节点，但是删除了根节点之后还怎么保持树的结构呢？所以我们实际上要做的是替换删除，也就是在这棵子树中找到一个节点的值，来替换要删除的子树的根的值，最后我们只需要把已经把值存到根节点的那个节点删除就行了，这样就有转变为了前两种情况。

那么对于一颗搜索二叉树的根节点来说，把哪个值替换过来之后能够保证根节点还是比左子树的所有节点大，同时比右子树的所有节点小呢？

我们只需要拿到左子树的最大节点，或者右子树的最小节点就行。为什么呢？我们把左子树的最大节点的值放到根节点中，他的值比左子树的所有的值都要大（除了他自己，但是他自己一会要删除），同时由于他是左子树中拿出来的值，那么他一定是要比右子树的所有的值要小的，所以替换之后，还是满足搜索二叉树的规则。

对于每一棵子树其实都可以这样使用替换法进行删除，前面的两种情况也可以这样做，只是前面几年的两种情况用替换法删除的话要增加太多的判断，不值得。同时，由于我们并没有实际删除子树的根节点，所以就算我们要删除的值是整棵树的根节点，我们也不需要改变_root指向的节点，我们是将他里面的数据进行狸猫换太子了。但是，当把节点删完之后，我们还是需要将_root置为空的。

但是这里还有一种情况，就是左子树的最大节点就是左子树的根

那么这时候还是使用前两种情况的方法进行删除，因为这样一来要删除的就是左子树的根节点，而这种情况的话左子树又是只有一棵子树。

	//删除
	bool erase(K key)//删除的值如果不存在就返回 false
	{
		assert(_root); //不能对一棵空树进行删除操作

		//首先找到要删除的节点，同时也要保存父节点
		Node* parent = nullptr;
		Node* cur = _root;
		while (cur)
		{
			if (key == cur->_key)
				break;
			else
			{
				parent = cur;//判断完不相等之后才更新父节点
				if (key < cur->_key)
					cur = cur->_left;
				else
					cur = cur->_right;
			}
		}
		if (!cur) //cur为nullptr说明没有找到要删除的节点，返回false
			return false;

		//删除cur
		//第一种情况 单支树的根节点或者叶子节点
		if (cur->_left == nullptr || cur->_right == nullptr)
		{
			if (parent == nullptr) //parent为空，意味着cur是整棵树的根节点
			{
				if (cur->_left) //左不为空就把根节点替换为左树的根节点
				{
					_root = cur->_left;
					delete cur;
					return true;
				}
				else
				{
					_root = cur->_right; //这里也包括了根节点的左右都为空，这时候就把根节点置为空了
					delete cur;
					return true;
				}
			}
			//走到这里说明不是根节点
			if (cur->_left == nullptr) //左子树为空，把右子树接到父节点的原位置
			{
				if (cur == parent->_left)
					parent->_left = cur->_right;
				else
					parent->_right = cur->_right;
			}
			else //右子树为空，把左子树街道父节点的原位置 ,这里也把cur是叶子节点的情况一并解决了
			{
				if (cur == parent->_left)
					parent->_left = cur->_left;
				else
					parent->_right = cur->_left;
			}
			//最后删除节点
			delete cur;
			return true;
		}
		else//删除左右子树都不为空的根节点
		{
			//首先要找到左子树的最大值或者右子树的最小值
			//左子树的最大值就是左子树的右路最远节点
			Node* del = cur->_left;
			while (del->_right)
			{
				del = del->_right;
			}
			//将要删除的节点的数据替换到根节点
			cur->_key = del->_key;
			//然后删除del
			if (del == cur->_left) //如果左子树的最大值就是左子树的根，证明左子树只有左子树，那么就直接进行删除和替换
			{
				cur->_left = del->_left;
				delete del;
				return true;
			}
			else
			{
				//要删除左子树的最大节点了
				cur = cur->_left;
				while (cur->_right != del)
					cur=cur->_right;
				cur->_right = nullptr;
				delete del;
				return true;
			}

		}
	}

删除的方法主要是要考虑几种情况来删除。这时候我们也可以进行测试

void testBST2()
{
	BSTree<int> b;
	int arr[] = { 5,3,6,7,1,3,5,0,9,8,2,4 };
	for (auto e : arr)
		b.insert(e);
	b.Inorder();
	for (int i=0;i<10;++i)
	{
		b.erase(i);
		b.Inorder();
	}
	//b.erase(0); //再测试一下空树删除是否会断言失败
}

目前来看删除的逻辑是没有问题的。

而其他的一些接口也没必要实现了，比如迭代器区间构造，这只需要不断插入数据就行了，同时我们要知道搜索二叉树是不支持对节点进行修改的，因为这可能会破坏搜索二叉树的规则。

既然搜索二叉树也是一棵二叉树，我们是不是可以把它的接口都实现成递归的形式呢？

递归查找没什么好说的

	//递归查找
	Node* findR(K key)
	{
		return findR(_root,key);
	}
    //递归查找子函数
	Node* findR(Node* root, K key)
	{
		if (root == nullptr)
			return nullptr;
		if (key == root->_key)
			return root;
		else if (key < root->_key)
			return findR(root->_left, key);
		else
			return findR(root->_right,key);
	}

递归的插入如果按照我们以前的C语言的写法，其实很麻烦，需要穿三个参数，root，parent ，和key，因为我们当root走到nullptr之后，需要将新插入的节点连接到parent上，所以需要传三个参数，但是当我们学习了C++的引用之后，我们就不需要这么麻烦了，我们可以用parent的left或者right的引用来传参给root，这样一来，root走到空了之后还是找到了对应的位置，那么就可以进行插入，插入到的节点我们直接给 root 就行，因为root就是他的父节点的left或者right的引用，修改root 就是修改parent的left或者right

    //递归插入
	bool insertR(K key)
	{
		return insertR(_root,key);
	}

    //递归插入子函数
	bool insertR(Node*& root, K key)
	{
		if (root == nullptr) //走到空了说明到了要插入的位置
		{
			Node* newnode = new Node(key);
			root = newnode;
			return true;
		}
		if (key == root->_key)
			return false;

		if (key < root->_key)
			return insertR(root->_left,key);
		else
			return insertR(root->_right,key);
	}

递归删除其实他的递归还是主要体现在查找要删除的节点上，他的节点的递归删除其实没有说明难度，还是那两种情况，只不过第二种情况的删除我们进行替换之后可以直接递归来删除。


	//递归删除
	bool eraseR(K key)
	{
		assert(_root);
		return eraseR(_root,key);
		
    }

    //递归删除子函数
	bool eraseR(Node*& root, K key) //还是使用引用传参，便于直接修改与父节点的链接关系
	{
		if (root == nullptr) //找不到该节点
			return false;
		if (key == root->_key)//删除
		{
			if (root->_left == nullptr || root->_right == nullptr)//左子树或者右子树为空
			{
				Node* del = root; //root就是要删除的节点
				if (root->_left)
					root = root->_left;
				else
					root = root->_right;
				//托孤完之后删除节点
				delete del;
				return true;
			}
			else//换节点数据
			{
				//还是找左子树的最大值
				Node* del = root->_left;
				while (del->_right)
				{
					del = del->_right;
				}
				//找到最大值之后还是替换
				root->_key = del->_key;
				//转换成递归删除左子树的最大值的节点
				return eraseR(root->_left,root->_key);
			}
		}

		if (key < root->_key)
			eraseR(root->_left,key);
		else
			eraseR(root->_right, key);
	}

虽然搜索二叉树的这些接口可以实现递归版本，但是我们实际上还是不会写成递归，有递归就有可能会栈溢出，一般情况下，能用迭代解决的问题就不用递归解决。

最后就是析构函数，析构函数我们注意后续遍历就行了

	~BSTree()
	{
		clear(_root);
	}
	//清除所有节点
	void clear(Node*& root) //还是采用引用传参，方便删除之后直接置空
	{
		if (root == nullptr)
			return;
		//后序
		clear(root->_left);
		clear(root->_right);
		delete root;
		root = nullptr;
	}

拷贝构造的话就是前序遍历的顺序

	//拷贝构造
	BSTree(const BSTree& bt)
	{
		_root = copy(bt._root);
	}
	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;

		//前序
		Node* newnode = new Node(root->_key);
		newnode->_left = copy(root->_left);
		newnode->_right = copy(root->_right);
		return newnode;
	}

赋值重载就更简单了，直接现代写法，传值传参，然后交换两个根节点。

	//赋值重载
	BSTree operator=(BSTree bt)
	{
		swap(_root,bt._root);
	}

1.3 应用模型

搜索二叉树和我们以前学的数据结构已经有一些本质性的区别，之前学的容器我们叫做序列式容器，这些容器以线性表的形式存储数据，数据与数据之间其实没有联系，单纯存储数据。而搜索二叉树以及我们后面要学的从搜索二叉树发展而来的一些容器我们叫做 关联式容器，顾名思义，就是数据与数据之间存在很强的关联，而不是单纯存储，每一个数据的位置都符合一定的规则。

那么搜索二叉树具体有什么应用呢？

1 K模型：K模型就是只有key作为关键码，树的节点中只需要存储key即可。关键码就是我们搜索的值。

具体的应用场景比如：所有单词的集合，我们可以以每个单词作为key，构建一棵搜索二叉树，方便我们检索某个字符串是不是单词。

2 KV模型：每一个关键码 key ，都有与之对应的值 value ，即节点存储的是 <key ,value> 的键值对。

这种方式我们用的比较多，具体的引用场景比如我们的英汉也就是单词与翻译的对应关系，我们可以以每一个单词作为 key ，然后以他的翻译作为 value，这样我们就能很方便的查找一个单词的中文翻译。或者我们也可以用来统计某个单词出现的次数，我们不断将单词与次数进行插入，初始的value为1，如果遇到相同的单词，不是插入失败，而是在将该节点的键值对中的value 加1。最后，我们如果要查询一个单词出现的次数，就可以搜索该单词，与之对应的 value 就是该单词出现的次数

我们上面模拟实现的搜索二叉树就是K模型，如果要改造成KV模型也很简单，就是在每个节点中存储的是一个键值对而不是单纯的key，但是由于我们还没有学习键值对，也可以直接存两个变量key和value，也是一一对应的。改造的过程我们只需要修改一下构造和插入这两类函数就跟可以了

    //要修改的的地方

template<typename K,typename V>
struct BSTNode
{
	K _key;
	V _value;
	BSTNode* _left;
	BSTNode* _right;

	BSTNode(K key ,V value=1)
		:_key(key), _value(value), _left(nullptr), _right(nullptr)
	{}
};


template<typename K ,typename V>

	typedef BSTNode<K,V> Node;


	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;

		//前序
		Node* newnode = new Node(root->_key,root->value);
		newnode->_left = copy(root->_left);
		newnode->_right = copy(root->_right);
		return newnode;
	}

	//插入
	bool insert(const K& key)
	{
		//判断是否为空树
		if (_root == nullptr)
		{
			Node* newnode = new Node(key);
			_root = newnode;
			return true;
		}
		//不是空树，需要找到插入的位置
		Node* parent = nullptr;//保存最终位置的父节点，用来连接新节点
		Node* cur = _root;

		while (cur)
		{
			if (cur->_key == key)
			{
				cur->_value++; //value++
				return false;
			}
			else
			{
				parent = cur; //不相等时才更新parent
				if (key < cur->_key)
					cur = cur->_left;
				else
					cur = cur->_right;
			}
		}
		//走到这里说明cur遍历到了nullptr，也就是说 parent 就是新节点的父节点
		cur = new Node(key);
		//判断一下是连接到左边还是右边
		if (key < parent->_key)
			parent->_left = cur;
		else
			parent->_right = cur;

		return true;
	}

	Node* copy(Node* root)
	{
		if (root == nullptr)
			return nullptr;

		//前序
		Node* newnode = new Node(root->_key,root->value);
		newnode->_left = copy(root->_left);
		newnode->_right = copy(root->_right);
		return newnode;
	}

	//递归插入子函数
	bool insertR(Node*& root, K key)
	{
		if (root == nullptr) //走到空了说明到了要插入的位置
		{
			Node* newnode = new Node(key);
			root = newnode;
			return true;
		}
		if (key == root->_key)
		{
			root->_value++; //value++
			return false;
		}
		if (key < root->_key)
			return insertR(root->_left, key);
		else
			return insertR(root->_right, key);
	}

这样我们就可以首先一个统计单词出现次数的搜索二叉树了。

2 二叉树的oj题

这种就是很简单的前序遍历的顺序，只不过每一棵子树构建的字符串都需要用括号括起来

初步转化

    string tree2str(TreeNode* root) {
        string ret;
        if(root==nullptr)
        return ret;
        //初步转化构建
        //前序遍历
        ret+=root->val+'0';

        //左右子树
        ret+='(';
        ret+=tree2str(root->left);  //左子树得到的字符串
        ret+=')';
        
        ret+='(';
        ret+=tree2str(root->right); //右子树得到的字符串
        ret+=')';

        return ret;
    }

进行初步转化之后，就得到了

但是题目要求没有必要的括号要删除，那么那些括号是没有必要的呢？一般来说，如果字数是空树，那么是没有必要用括号括起来的，但是这里有有一个例外，就是当左树为空但是右树不为空的时候，左树虽然是一棵空树，但还是要有一对括号用来占位的。而右树就很随意了，只要右树为空，就可以省略括号。

    string tree2str(TreeNode* root) {
        string ret;
        if(root==nullptr)
        return ret;
        //初步转化构建
        //前序遍历
        ret+=root->val+'0';
        if(root->left||root->right) //左树或者右树有一边不为空，左树的括号就不能省略
        {
            ret+='(';
            ret+=tree2str(root->left);  //左子树得到的字符串
            ret+=')';
        }    
        if(root->right)//右树为空就省略空括号
        {
            ret+='(';
            ret+=tree2str(root->right); //右子树得到的字符串
            ret+=')';
            return ret;
        }
        return ret;
    }

但是这个题还有一个坑，就是节点的数据有可能是负数，如果是负数的话，就不能单纯的用

root->val+'0'来表示了，有一个简单的办法就是用C语言的to_string函数.

最终代码


class Solution {
public:
   
    string tree2str(TreeNode* root) {
        string ret;
        if(root==nullptr)
        return ret;
        //初步转化构建
        //前序遍历
        ret+=to_string(root->val);
        if(root->left||root->right) //左树或者右树有一边不为空，左树的括号就不能省略
        {
            ret+='(';
            ret+=tree2str(root->left);  //左子树得到的字符串
            ret+=')';
        }    
        if(root->right)//右树为空就省略空括号
        {
            ret+='(';
            ret+=tree2str(root->right); //右子树得到的字符串
            ret+=')';
            return ret;
        }
        return ret; 
    }
};

这里的层序遍历要求我们每一层单独放在一个vector来返回。层序遍历我们还是很好写的，用一个队列就能实现，但是如何标识每个节点的层数呢？

最简单的方法就是我们在队列中不只放节点指针，还把节点的层数放进去，以此来分层。


struct Node
{
    TreeNode* _node; //节点
    int _floor; //节点所在层数
    Node(TreeNode*node,int floor)
    :_node(node),_floor(floor)
    {}
};


class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ret;
        if(!root)
        return ret;
        //规定根节点的层数为0，便于放进二维数组中
        queue<Node> q;
        q.push(Node(root,0));
        while(!q.empty())
        {
            Node front=q.front();
            q.pop();
            if(front._floor>=ret.size())//判断是否要扩容
            {
                ret.resize(front._floor+1);
            }
            ret[front._floor].push_back(front._node->val);
            if(front._node->left)
            q.push(Node(front._node->left,front._floor+1)); //子节点的层数加1
            if(front._node->right)
            q.push(Node(front._node->right,front._floor+1)); //子节点的层数加1
        }
        return ret;
    }
};

但是其实还有一种更简单的方式，我们知道，当第 n 层的节点全部从队列里面取出来的的时候，那么意味着第 n+1 层的节点已经全部入队列了，那么第 n+1层的节点的个数就是队列此时的size，这样一来我们就能用一个变量来表示当前层数还有几个节点在队列中，当数量变为 0 的时候，就意味着要更新该变量为下一层的节点的个数了。

如图，以此类推，当q为空的时候就结束了。


class Solution {
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
        vector<vector<int>> ret;
        if(!root)
        return ret;

        queue<TreeNode*> q;
        q.push(root);
        int count=q.size();
        while(!q.empty())
        {
            vector<int> floor; //保存当前层的节点值
            while(count>0)
            {
                TreeNode* front = q.front();
                floor.push_back(front->val);
                q.pop();
                count--;
                if(front->left)
                q.push(front->left);
                if(front->right)
                q.push(front->right);            
            }
            //count为0时更新count，并把当前层的数组放进总体的数组中
            ret.push_back(floor);
            count=q.size();
        }
        return ret; 
    }
};

这个题需要我们返回自底向上的层序遍历，如果真的按照自底向上的遍历顺序来搞，肯定会十分复杂。那么我们其实是可以利用上一个题的自顶向下的层序遍历，把结果逆置一下就行了。

class Solution {
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
        vector<vector<int>> ret;
        if(!root)
        return ret;

        queue<TreeNode*> q;
        q.push(root);
        int count=q.size();
        while(!q.empty())
        {
            vector<int> floor; //保存当前层的节点值
            while(count>0)
            {
                TreeNode* front = q.front();
                floor.push_back(front->val);
                q.pop();
                count--;
                if(front->left)
                q.push(front->left);
                if(front->right)
                q.push(front->right);            
            }
            //count为0时更新count，并把当前层的数组放进总体的数组中
            ret.push_back(floor);
            count=q.size();
        }
        reverse(ret.begin(),ret.end()); //结果逆置一下
        return ret; 
    }
};

求二叉树的两个节点的最近公共祖先。我们最容易想到思路就是把两个节点到根的路径给保存下来，然后对比，就能很容易找到最近公共祖先。但是如何把路径求出来呢？还是用递归吗，如果该节点在当前节点的左树或者右树，就将该节点保存起来。

class Solution {
public:
    //求节点路径
    bool Getpath(TreeNode* root,TreeNode* node,vector<TreeNode*>& path)
    {
        if(!root)
        return false ;
        if(root==node) //节点自身也是自己的祖先节点
        {
            path.push_back(root);
            return true;
        }
        else if(Getpath(root->left,node,path)||Getpath(root->right,node,path))
        {
            path.push_back(root);
            return true;
        }
        return false;

    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        vector<TreeNode*> ppath;
        Getpath(root,p,ppath);
        vector<TreeNode*> qpath;
        Getpath(root,q,qpath);
        //注意递归求出来的路径是反着放的
        int pend=ppath.size()-1;
        int qend=qpath.size()-1;
        while(pend>=0&&qend>=0)
        {
            if(ppath[pend]==qpath[qend])
            {
                pend--;
                qend--;
            }
            else
            break;
        } 
        return ppath[pend+1];

    }
};

这个题该有一种方法，判断两个节点是否当前节点的左右子树，如果两个节点都在左子树或者都在右子树，就说明当前虽然是公共祖先节点，但是不是最近的。而当两个节点分别在当前节点的左右子树或者其中一个节点就是根同时另一个节点也在当前子树，就说明是最近公共祖先节点


class Solution {
bool IsInTree(TreeNode*root,TreeNode*node)
{
    if(!root)
        return false;
    if(node==root)
        return true;
    else
    return IsInTree(root->left,node)||IsInTree(root->right,node);
}

public:
    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        if(p==root||q==root)
        return root;

        bool qleft=IsInTree(root->left,q);   //q是否在左子树 
        bool qright=IsInTree(root->right,q); //q是否在右子树 
        bool pleft=IsInTree(root->left,p);   //p是否在左子树 
        bool pright=IsInTree(root->right,p); //p是否在右子树 
        
        if((pleft&&qright)||(qleft&&pright)) //在左右两边
            return root;
        else //都在一边
        {
            if(qleft)
                return lowestCommonAncestor(root->left,p,q);
            else
                return lowestCommonAncestor(root->right,p,q);
        }
    }
};

这种方法虽然思路很简单，但是在判断是否在左子树和是否在右子树的时候会有过多的重复操作，所以效率不如直接求路径高。

同时，如果这棵树是二叉搜索树的话，我们直接使用数据的大小来判断会更加简单。

这个题就是让我们把搜索二叉树变成一个有序的双向链表，但是我们要直接用这棵树的节点来改造，不能增加新的节点，把节点的 left 看成是链表的prev，把right看成是链表的next。

首先我们能想到的思路就是中序遍历来解决问题，对于一个节点来说，对于一个子树的根节点来说，如果他的左子树不为空，那么他的 left 要指向左子树的最右节点，左子树的最右节点的right也要链接到该节点。如果他的右子树为空，那么该节点的 right 就要链接到他的父节点。如果他的右子树不为空，那么该节点的right就要连接到右子树的最左节点，同时右子树的最左节点的left也要连接到该节点。

这就意味着，要保存左子树的最右节点来连接到节点的left，要保存右子树的最左节点来链接到节点的right，同时也要保存父节点以防右子树为空。

当前逻辑看着就很复杂，对于上面的三种情况，我们是否需要用四个变量来保存所谓的四个节点呢？我们可以仔细思考一下中序的遍历顺序。我们访问根节点的前一个访问的节点就是左子树的最右节点，访问完根节点之后的下一个要访问的节点就是右子树的最左节点。如果左右子树都为空，那么访问该节点前的上一个被访问的节点不就是他的父节点吗？所以我们上面说的三个特殊的节点其实都可以用两个节点来概括，就是中序遍历中当前要访问的节点和前一个访问的节点。

前一个访问的节点的right要链接到当前节点，当前节点的left要链接到前一个节点。

对于叶子节点，访问他的时候就只需要更新prev，因为他的链接关系要在访问他的下一个节点时才修改。

同时要注意的是，他要改成一个双向循环链表，所以最后我们还要将头节点与尾节点链接起来。虽然我们在链接的时候没有关注头节点和尾节点，但是我们目前知道的就是，头节点的left一定是为空的，因为头节点就是最左节点，我们是没有动最左节点的left的，而尾节点是最右节点，最右节点的right我们也是没有动的，所以他还是原来的nullptr，因为不管哪个节点的right，都要在下一个访问的节点才动。所以我们拿着root不断往左走和不断往右走就能找到头和尾。

class Solution {
public:
    void toList(Node*cur,Node*&prev)
    {
        if(!cur)
        return;

        //中序遍历
        toList(cur->left,prev);

        cur->left=prev;
        if(prev)
        prev->right=cur;
        prev=cur;

        toList(cur->right,prev);
    }

    Node* treeToDoublyList(Node* root) {
        if(!root)
        return nullptr;

        //定义prev，用来引用传参，修改prev
        Node* prev =nullptr;
        toList(root,prev);
        //找头尾进行链接
        Node*head=root;
        while(head->left)
            head=head->left;
       
        Node* tail=root;
        while(tail->right)
            tail=tail->right;
    
        head->left=tail;
        tail->right=head;
        return head;
    }
};

其实如果题目没有空间复杂度的要求的话，我们还有一种更简单的方法，就是中序遍历将所有的节点存在一个vector里，然后再来修改链接关系，这种方法简单粗暴。


class Solution {
public:
    void tolist(Node* root,vector<Node*>& ret)
    {
        if(!root)
        return;
        if(root->left)
        tolist(root->left,ret);
        ret.push_back(root);
        if(root->right)
        tolist(root->right,ret);

    }
    
    Node* treeToDoublyList(Node* root) {
        if(!root)
        return root;
        vector<Node*> ret ;
        tolist(root,ret);
        for(int i=0;i<ret.size();++i)
        {
            if(i<ret.size()-1)
            ret[i]->right=ret[i+1];
            if(i>0)
            ret[i]->left=ret[i-1];
        }
        ret[0]->left=ret[ret.size()-1];
        ret[ret.size()-1]->right=ret[0];
        return ret[0];
    }
};

用前序序列和中序序列构造二叉树，这个题其实我们在二叉树基础部分就已经讲过思路了，我们知道，前序是能够确定根节点的，而中序则能够通过根节点来确定该节点的左右子树的区间。

如图：

首先确定根，然后前序遍历的第二个节点就是左子树的根，

其实只要构建完根节点并划分完区间之后，我们就能用分治的思想来解决左右子树的构建了。

class Solution {
public:
    TreeNode* Build(vector<int>&preorder,int& index,vector<int>&inorder ,int left,int right)
    {
        //首先判断中序区间是否有数据
        if(left>right)
        return nullptr;

        //构建根节点
        TreeNode* root =new TreeNode(preorder[index++]);
        //在中序区间以根节点为间隔，划分左右子树的区间
        int root_index=0;
        for(;inorder[root_index]!=root->val;++root_index)
        {}
    
        //构建左右子树
        root->left=Build(preorder,index,inorder,left,root_index-1);
        root->right=Build(preorder,index,inorder,root_index+1,right);
        return root;
    }

    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
        int index=0; //index是所有栈帧共享的，随着根节点的创建不断往后移动
        int left=0;
        int right=inorder.size()-1; //left和right是每个栈帧所独有的,不影响上一层,传值传参
        TreeNode*root=Build(preorder,index,inorder,left,right);


        return root;

    }
};

再来做一个类似的

中序和后续构造二叉树其实跟前序和中序构建没什么区别，无非就是根节点从后往前看，然后是先构建右子树在构建左子树，区别不是很大们直接给出代码。

class Solution {
public:
    TreeNode* Build(vector<int>& postorder,int& index, vector<int>& inorder,int left,int right)
    {
        if(left>right)
        return nullptr;
        //先构建根节点
        TreeNode* root=new TreeNode(postorder[index--]);
        int root_index=0;
        for(;inorder[root_index]!=root->val;++root_index)
        {}

        //先构建右子树，再构建左子树
        root->right=Build(postorder,index,inorder,root_index+1,right);
        root->left=Build(postorder,index,inorder,left,root_index-1);
        return root;
    }

    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
        int left=0;
        int right=inorder.size()-1;
        int index=postorder.size()-1; 
        
        TreeNode*root=Build(postorder,index,inorder,left,right); 

        return root;
    }
};

不使用递归，使用迭代完成前序遍历

迭代实现的前序遍历，我们可以把一棵树分为左路节点，和左路节点的右子树。那么我们需要用一个数据结构来保存左路节点。由于是前序遍历，所以我们在将左路节点放进这个数据结构的时候之前要先访问这个节点，但是我们知道，前序遍历的时候，越往深处的左路节点的右子树是要先被访问的，也就是后访问的左路节点我们要先访问它的右子树，右子树的访问方法又和前面的一样，所以我们需要一个后进先出的数据结构，也就是栈来存储这些访问过的左路节点。对于栈中的节点，我们只需要访问它的右子树

class Solution {
public:
    vector<int> preorderTraversal(TreeNode* root) {
        stack<TreeNode*> st;
        TreeNode*cur=root;
        vector<int> ret;

        while(cur||!st.empty()) //栈不为空或者当前要访问的树不为空就继续
        {
            //左路节点全部访问并入栈
            while(cur)
            {
                ret.push_back(cur->val);
                st.push(cur);
                cur=cur->left;
            }
            //拿出栈顶的元素
            cur=st.top();
            st.pop();
            cur=cur->right; //访问左路节点的右子树
        }

        return ret;
    }
};

中序遍历，但是还是要非递归实现，思路还是和前序的思路一样，把一棵树的访问分为左路节点和左路节点的右子树来进行。但是外面拿他的左路节点的时候先不访问，而是直接入栈，在出栈的时候访问该节点并访问该节点的右子树，这样才符合中序遍历的顺序。

class Solution {
public:
    vector<int> inorderTraversal(TreeNode* root) {
        vector<int> ret;
        TreeNode* cur=root;
        stack<TreeNode*> st;
        while(cur||!st.empty())
        {
            //左路节点先入栈，但是不访问，出栈的时候才是访问他的时机
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            cur=st.top();
            st.pop();
            //访问左路节点和他的右子树
            ret.push_back(cur->val);
            cur=cur->right;
        }
        return  ret;

    }
};

二叉树的非递归后序遍历。思路还是用的前面的思路，访问一棵树首先要分为左路节点和左路节点的右子树。

左路节点入栈的时候也不能直接访问。但是出栈的时候就能访问了吗？不一定，因为如果该节点的右子树不为空的话，那么要先访问完他的右子树才能访问这个节点，甚至当该节点的右子树不为空的时候，该节点都给还不能出栈，因为出栈的话右子树访问完了也找不到该节点访问了。每一个节点都是这样，所以我们必须要对节点做一个标记，看他的右子树是否访问完了。最简单的标记方式就是栈里面放一个键值对，保存一个结点指针和一个标记位，当我们取到该节点并且开始去访问他的右树的时候，我们就把标记位更新。这样一来，对于每一个栈顶的键值对，我们首先要看的是该节点右子树是否为空，如果为空那么就直接出栈并且访问数据。但是如果不为空，那么就需要先修改标记位，然后访问他的右子树。

 struct Node{
    TreeNode* _node;
    int _flag=0; //0表示右子树还没访问，1表示右子树已经访问完了
    Node(TreeNode*node,int flag=0)
    :_node(node),_flag(flag)
    {}
 };
 
class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> ret;
        stack<Node> st;
        TreeNode*cur=root;
        while(cur||!st.empty())
        {
            //左路节点入栈
            while(cur)
            {
                st.push(Node(cur)); //默认是未访问右子树，flag=0
                cur=cur->left;
            }
            //取出栈顶元素
            Node& top=st.top(); //注意这里要的是引用
            //先判断右子树是否为空。为空就不需要管标记，直接访问
            if(top._node->right==nullptr||top._flag==1)
            {
                ret.push_back(top._node->val);
                st.pop();
                //不需要更新cur，因为cur走到这里已经是nullptr了
            }
            else //flag==0
            {
             
                cur=top._node->right;
                top._flag=1;
            }
        }
        return ret;
    }
};

这种方法虽然可以完成，但是还是有点复杂。这里还有一种更简单的方法，我们可以参考上面的那个将搜索二叉树改为链表的题，我们只需要一个prev指针就能够完成标记和链接的作用。而我们这里的后序遍历也是一样的，我们要访问一个节点，如果他的右子树为空，那么是可以直接访问的，但是如果他的右子树不为空且没有被访问，那么我们就需要先访问他的右子树，如何判断该节点的右子树有没有被访问呢？很简单，还是判断上一个访问的节点，如果上一个访问的节点就是他的右子树的根，那么就说明了他的右子树已经访问完了。

代码如下

class Solution {
public:
    vector<int> postorderTraversal(TreeNode* root) {
        TreeNode*prev=nullptr;
        TreeNode*cur=root;
        vector<int> ret;
        stack<TreeNode*>st;
        while(cur||!st.empty())
        {
            //左路节点入栈
            while(cur)
            {
                st.push(cur);
                cur=cur->left;
            }
            //取出栈顶元素
            cur=st.top();
            //判断上一个访问的节点是否是他的右子树的根 , 或者他的右子树是否为空
            if(prev==cur->right||cur->right==nullptr)
            {
                //直接访问
                prev=cur; //更新prev
                st.pop();
                ret.push_back(cur->val);
                cur=nullptr; //这里不更新cur为栈顶节点，懒得考虑栈为空了
            }
            else
            {
                cur=cur->right;//访问右子树
            }

        }
    return ret;
    }
};