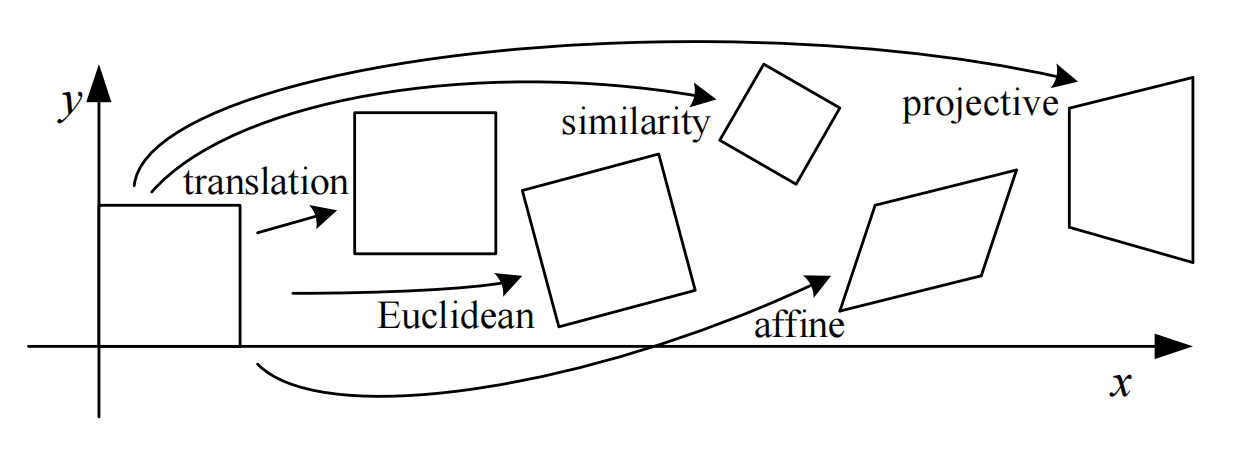
2D运动模型
其中相应的运动可以通过变换矩阵实现
基本运算
平移
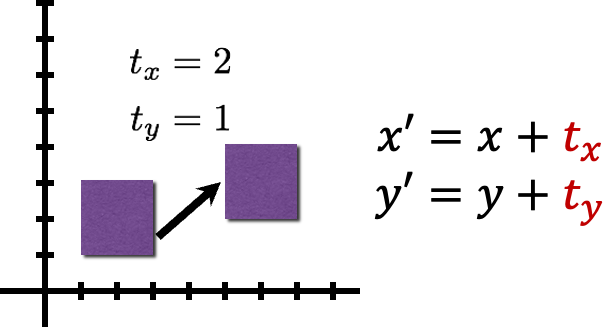
[ x ′ y ′ 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] = [ I t 0 T 1 ] [ x y 1 ] \begin{aligned} \begin{bmatrix}x'\\y'\\1\end{bmatrix} &=\begin{bmatrix}1&0&t_x\\0&1&t_y\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}\\ &=\begin{bmatrix}I&t\\0^T&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} \end{aligned} x′y′1 = 100010txty1 xy1 =[I0Tt1] xy1
I : 2 × 2 的单位矩阵 I:2\times2的单位矩阵 I:2×2的单位矩阵
t = [ t x , t y ] T : 2 t=\begin{bmatrix}t_x,t_y\end{bmatrix}^T:2 t=[tx,ty]T:2D平移向量
缩放
缩放:坐标系的每个轴乘以一个标量/缩放因子
均匀缩放:所有轴的缩放因子相同
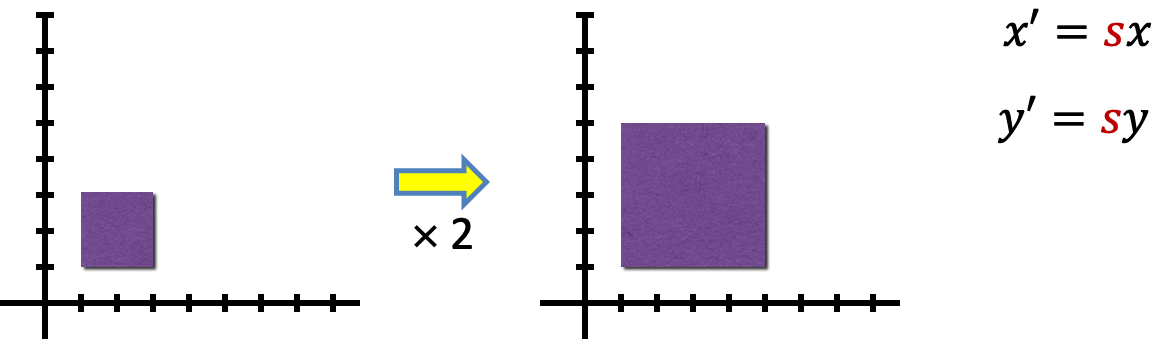
[ x ′ y 1 ] = [ s 0 0 0 s 0 0 0 1 ] [ x y 1 ] = [ s I 0 0 T 1 ] [ x y 1 ] \begin{aligned}\begin{bmatrix}x^{\prime}\\y\\1\end{bmatrix}&=\begin{bmatrix}s&0&0\\0&s&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}\\&=\begin{bmatrix}sI&0\\0^{\mathrm{T}}&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}\end{aligned}
x′y1
=
s000s0001
xy1
=[sI0T01]
xy1
非均匀缩放:不同轴的缩放因子不同
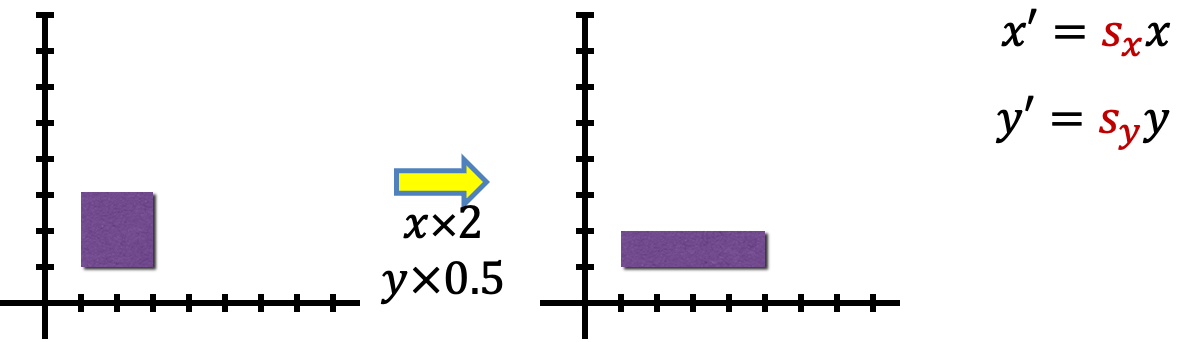
[ x ′ y ′ 1 ] = [ s x 0 0 0 s y 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}{s_x}&0&0\\0&{s_y}&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}
x′y′1
=
sx000sy0001
xy1
错切
方形变平行四边形,
x轴不变,沿y轴方向错切

[ x ′ y ′ 1 ] = [ 1 0 0 β y 1 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}1&0&0\\\beta_y&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}
x′y′1
=
1βy0010001
xy1
y轴不变,沿x轴方向错切

[ x ′ y ′ 1 ] = [ 1 β x 0 0 1 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}1&{\beta_x}&0\\0&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}
x′y′1
=
100βx10001
xy1
任意一边都可以被拉长

[ x ′ y ′ 1 ] = [ 1 β x 0 β y 1 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}1&{\beta_x}&0\\{\beta_y}&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix}
x′y′1
=
1βy0βx10001
xy1
旋转

[ x ′ y ′ 1 ] = [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\end{bmatrix} \begin{bmatrix} x\\y\\1 \end{bmatrix}
x′y′1
=
cos(θ)sin(θ)0−sin(θ)cos(θ)0001
xy1
综上所述
| 平移 | 缩放 | 错切 | 旋转 |
|---|---|---|---|
| [ x ′ y ′ 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}1&0&\color{red}{t_x}\\0&1&\color{red}{t_y}\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′1 = 100010txty1 xy1 | [ x ′ y ′ 1 ] = [ s x 0 0 0 s y 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}\color{red}{s_x}&0&0\\0&\color{red}{s_y}&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′1 = sx000sy0001 xy1 | [ x ′ y ′ 1 ] = [ 1 β x 0 β y 1 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}1&\color{red}{\beta_x}&0\\\color{red}{\beta_y}&1&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′1 = 1βy0βx10001 xy1 | [ x ′ y ′ 1 ] = [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\1\end{bmatrix}=\begin{bmatrix}\cos({\color{red}\theta})&-\sin({\color{red} \theta})&0\\\sin({\color{red} \theta})&\cos({\color{red}\theta})&0\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′1 = cos(θ)sin(θ)0−sin(θ)cos(θ)0001 xy1 |
复合运算
可以通过矩阵乘法得到复杂变换,矩阵乘法的顺序不同,可能会得到不同的变换。
欧式(刚体)变化
欧式(刚体)变换:(先)旋转+(后)平移
[ r 11 r 12 t x r 21 r 22 t y 0 0 1 ] = [ R ( θ ) t 0 T 1 ] = [ cos ( θ ) − sin ( θ ) t x sin ( θ ) cos ( θ ) t y 0 0 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] \begin{aligned}&\quad\begin{bmatrix}r_{11}&r_{12}&t_x\\r_{21}&r_{22}&t_y\\0&0&1\end{bmatrix}\\&=\begin{bmatrix}\boldsymbol{R}(\theta)&\boldsymbol{t}\\\boldsymbol{0}^\mathrm{T}&1\end{bmatrix}\\&=\begin{bmatrix}\cos(\theta)&-\sin(\theta)&t_x\\\sin(\theta)&\cos(\theta)&t_y\\0&0&1\end{bmatrix}\\&=\begin{bmatrix}1&0&\boldsymbol{t}_x\\0&1&\boldsymbol{t}_y\\0&0&1\end{bmatrix}\begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\end{bmatrix}\end{aligned}
r11r210r12r220txty1
=[R(θ)0Tt1]=
cos(θ)sin(θ)0−sin(θ)cos(θ)0txty1
=
100010txty1
cos(θ)sin(θ)0−sin(θ)cos(θ)0001
其中自由度为3
等距变换
[ x ′ y ′ w ′ ] = [ ε c o s θ − s i n θ t x ε s i n θ c o s θ t y 0 0 1 ] [ x y 1 ] \begin{bmatrix}x^{\prime}\\y^{\prime}\\w^{\prime}\end{bmatrix}=\begin{bmatrix}{\varepsilon}\mathrm{cos}\theta&-\mathrm{sin}\theta&{t}_x\\\varepsilon\mathrm{sin}\theta&\mathrm{cos}\theta&{t}_y\\0&0&1\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′w′ = εcosθεsinθ0−sinθcosθ0txty1 xy1
其中 ε \varepsilon ε为1或-1
不变量:(绝对)长度、角度、面积
相似变换
相似变换:均匀缩放+旋转+平移
[ a − b t x b a t y 0 0 1 ] = [ s R ( θ ) t 0 T 1 ] = [ s cos ( θ ) − s sin ( θ ) t x s sin ( θ ) s cos ( θ ) t x 0 0 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] [ s 0 0 0 s 0 0 0 1 ] \begin{aligned} &\quad\begin{bmatrix}a&-b&t_x\\b&a&t_y\\0&0&1\end{bmatrix}\\&=\begin{bmatrix}sR(\theta)&t\\0^\mathrm{T}&1\end{bmatrix}\\&=\begin{bmatrix}s\cos(\theta)&-s\sin(\theta)&t_x\\s\sin(\theta)&s\cos(\theta)&t_x\\0&0&1\end{bmatrix} \\ &=\begin{bmatrix}1&0&{t_x}\\0&1&{t_y}\\0&0&1\end{bmatrix}\begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\end{bmatrix}\begin{bmatrix}{s}&0&0\\0&{s}&0\\0&0&1\end{bmatrix} \end{aligned}
ab0−ba0txty1
=[sR(θ)0Tt1]=
scos(θ)ssin(θ)0−ssin(θ)scos(θ)0txtx1
=
100010txty1
cos(θ)sin(θ)0−sin(θ)cos(θ)0001
s000s0001
自由度为4
不变量: 长度的比例(相对长度)、角度、面积的比例、平行线
在刚体变换中:a2+b2=1
仿射变换
仿射变换:错切+均匀缩放+旋转+平移
[ a 11 a 12 t x a 21 a 22 t y 0 0 1 ] = [ s cos ( θ ) − s sin ( θ ) β y s cos ( θ ) β x − s sin ( θ ) t x s sin ( θ ) + s cos ( θ ) β y s sin ( θ ) β x + s cos ( θ ) t y 0 0 1 ] = [ 1 0 t x 0 1 t y 0 0 1 ] [ cos ( θ ) − sin ( θ ) 0 sin ( θ ) cos ( θ ) 0 0 0 1 ] [ s 0 0 0 s 0 0 0 1 ] [ 1 β x 0 β y 1 0 0 0 1 ] \begin{aligned} &\quad\begin{bmatrix}a_{11}&a_{12}&t_x\\a_{21}&a_{22}&t_y\\0&0&1\end{bmatrix}\\ &=\begin{bmatrix}s\cos(\theta)-s\sin(\theta)\beta_y&s\cos(\theta)\beta_x-s\sin(\theta)&t_x\\s\sin(\theta)+s\cos(\theta)\beta_y&s\sin(\theta)\beta_x+s\cos(\theta)&t_y\\0&0&1\end{bmatrix} \\ &=\begin{bmatrix}1&0&{t_x}\\0&1&{t_y}\\0&0&1\end{bmatrix}\begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\end{bmatrix}\begin{bmatrix}{s}&0&0\\0&{s}&0\\0&0&1\end{bmatrix}\begin{bmatrix}1&{\beta_x}&0\\{\beta_y}&1&0\\0&0&1\end{bmatrix} \end{aligned}
a11a210a12a220txty1
=
scos(θ)−ssin(θ)βyssin(θ)+scos(θ)βy0scos(θ)βx−ssin(θ)ssin(θ)βx+scos(θ)0txty1
=
100010txty1
cos(θ)sin(θ)0−sin(θ)cos(θ)0001
s000s0001
1βy0βx10001
自由度为6
保持了图像的“平行性”和“平直性”,即图像中原来的直线和平行线,变换后仍然保持原来的直线和平行线
不变量: 平行线、平行长度的比例、面积比例
射影变换
[ x ′ y ′ w ′ ] = [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] [ x y 1 ] \begin{bmatrix}x'\\y'\\w'\end{bmatrix}=\begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix}\begin{bmatrix}x\\y\\1\end{bmatrix} x′y′w′ = h11h21h31h12h22h32h13h23h33 xy1
不变量:线上4点的交比(比例的比例),直线仍然是直的
综上所述
| 群 | 矩阵 | 失真 | 不变性质 |
|---|---|---|---|
| 射影(8DOF) | [ h 11 h 12 h 13 h 21 h 22 h 23 h 31 h 32 h 33 ] \begin{bmatrix}h_{11}&h_{12}&h_{13}\\h_{21}&h_{22}&h_{23}\\h_{31}&h_{32}&h_{33}\end{bmatrix} h11h21h31h12h22h32h13h23h33 |  |
共点、共线、接触的阶:相交(1阶接触)、相切(二阶接触)、拐点(3阶接触)、交比 |
| 仿射(6DOF) | [ a 11 a 12 t x a 21 a 22 t y 0 0 1 ] \begin{bmatrix}a_{11}&a_{12}&t_x\\a_{21}&a_{22}&t_y\\0&0&1\end{bmatrix} a11a210a12a220txty1 | 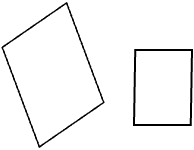 |
平行、面积比、平行线的长度比(如中点)、向量的线性组合(如形心)、无穷远直线l_∞_ |
| 相似(4DOF) | [ s r 11 s r 12 t x s r 21 s r 22 t y 0 0 1 ] \begin{bmatrix}sr_{11}&sr_{12}&t_x\\sr_{21}&sr_{22}&t_y\\0&0&1\end{bmatrix} sr11sr210sr12sr220txty1 | 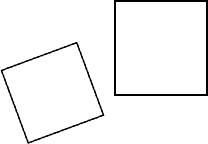 |
长度比、角度、虚圆点 I,J |
| 欧氏(3DOF) | [ r 11 r 12 t x r 21 r 22 t y 0 0 1 ] \begin{bmatrix}r_{11}&r_{12}&t_x\\r_{21}&r_{22}&t_y\\0&0&1\end{bmatrix} r11r210r12r220txty1 | 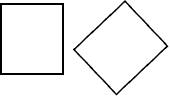 |
长度、面积 |
[!CAUTION]
给定同一条直线上的4个点 x 1 , x 2 , x 3 , x 4 x_1,x_2,x_3,x_4 x1,x2,x3,x4, 交比定义为:
cos ( x 1 , x 2 , x 3 , x 4 ) = ∥ x 1 x 3 ∥ ∥ x 1 x 4 ∥ ∥ x 2 x 3 ∥ ∥ x 2 x 4 ∥ \cos(x_1,x_2,x_3,x_4)=\frac{\|x_1x_3\|\|x_1x_4\|}{\|x_2x_3\|\|x_2x_4\|} cos(x1,x2,x3,x4)=∥x2x3∥∥x2x4∥∥x1x3∥∥x1x4∥
其中 ∥ x i x j ∥ = det [ x i 1 x j 1 x i 2 x j 2 ] \|x_{i}x_{j}\|=\det\begin{bmatrix}x_{i1}&x_{j1}\\x_{i2}&x_{j2}\end{bmatrix} ∥xixj∥=det[xi1xi2xj1xj2]