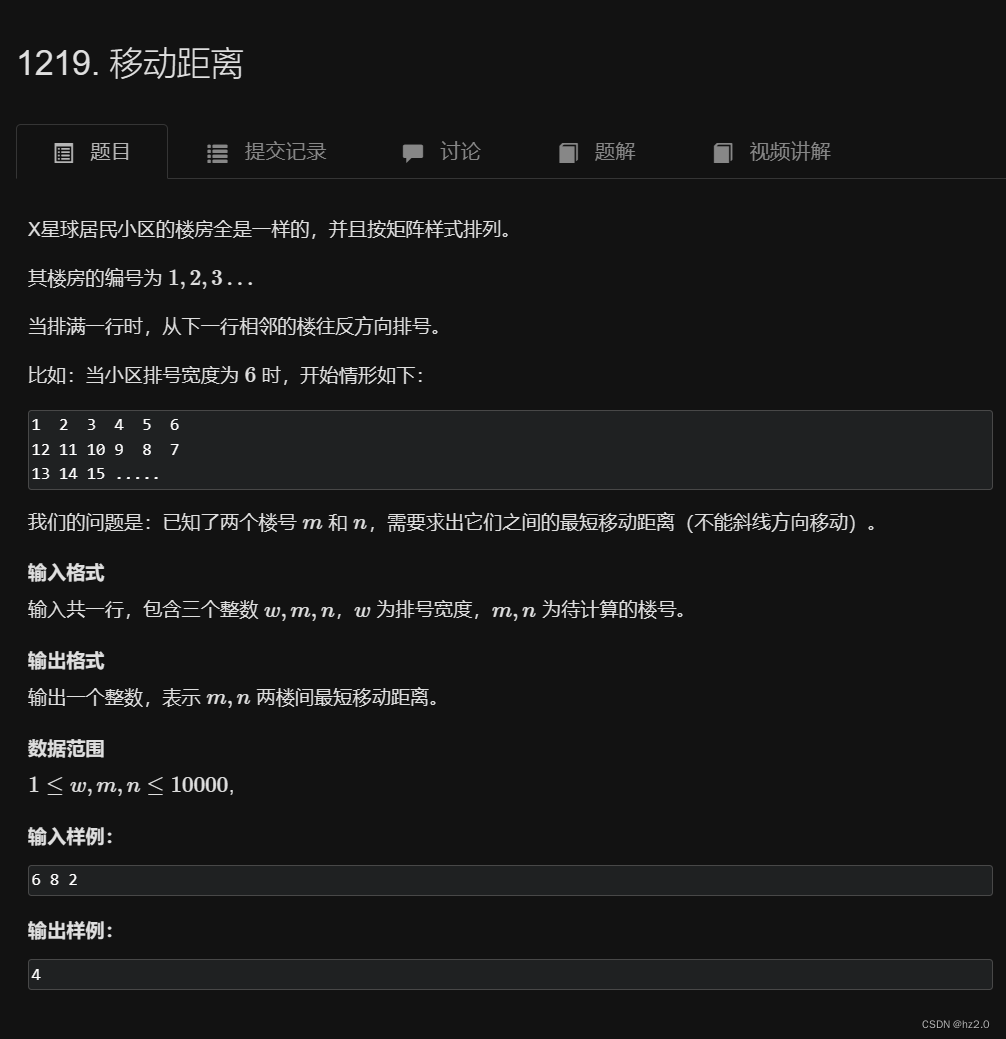
算法 {曼哈顿距离,切比雪夫距离}

算法 {曼哈顿距离,切比雪夫距离}

曼哈顿距离

定义

二维: 曼哈顿距离(A,B) = abs(A.x - B.x) + abs(A.y - B.y);
. 同时他也等于切比雪夫距离(A1,B1), 其中A1 = (A.x+A.y, A.x-A.y); B1 = (B.x+B.y, B.x-B.y)

三维: 曼哈顿距离(A,B) = abs(A.x - B.x) + abs(A.y - B.y) + abs(A.z - B.z);

算法

二维曼哈顿距离转切比雪夫距离|曼哈顿空间与切比雪夫空间的等距映射

#把绝对值给化简掉#
$曼哈顿距离(A,B)=abs(A.x-B.x)+abs(A.y-B.y)=MAX\{(A.x+A.y)-(p1.x+p1.y),(A.x-A.y)-(p1.x-p1.y),(p1.x-p1.y)-(A.x-A.y),(p1.x+p1.y)-(A.x+A.y)\}$;
令$Add[P]=P.x+P.y,Minus[P]=P.x-P.y$, 则 曼哈顿距离 ( A , B ) = M A X { A d d [ A ] − A d d [ B ] , A d d [ B ] − A d d [ A ] , M i n u s [ A ] − M i n u s [ B ] , M i n u s [ B ] − M i n u s [ A ] } 曼哈顿距离(A,B) = MAX\{ Add[A] - Add[B], Add[B] - Add[A], Minus[A] - Minus[B], Minus[B] - Minus[A]\} 曼哈顿距离(A,B)=MAX{Add[A]−Add[B],Add[B]−Add[A],Minus[A]−Minus[B],Minus[B]−Minus[A]};
继续化简得到: $MAX(abs(Add[A]-Add[B]),abs(Minus[A]-Minus[B]))$;
. 而这是式子 其实就等于(Add[A], Minus[A])与(Add[B], Minus[B])这两个点 之间的切比雪夫距离; (其实 即便你看不出这是切比雪夫距离, 此时也足矣了, 因为原来的曼哈顿距离 他是abs(x...) + abs(y...) 他是两个式子相加, 而此时 我们转换成了max( abs(Add...), abs(Minus...)) 他是两个式子取最大值, 这已经大大简化了, 因为你可以单独分析这两个式子, 即先得到abs(Add...)的最大值 然后再得到abs(Minus...)的最大值 (这两个步骤 是完全分开独立的), 两者取最大值 就是答案; 然而之前的式子 他俩是相加的 是不能分开的;

即对于任意点X, 令X1 = (X.x+X.y, X.x-X.y) = (Add[X], Minux[X]); 则任意两点A,B的曼哈顿距离 等于 A1,B1之间的切比雪夫距离;
. 令S0: 曼哈顿空间, S1: 切比雪夫空间, 则S0的任一点(x,y) -> S1的(x+y,x-y), 同样的S1的任意点(x,y) -> S0的((x+y)/2, (x-y)/2), 即得到了 S0, S1的一个等距映射;
因此 你去研究切比雪夫距离即可, 他有个非常重要的性质, 即各个维度是完全独立的, 是可以相互间分开的, 即切比雪夫距离(A,B) = max{ abs(A.x-B.x), abs(A.y-B.y)}, 然后你独立的求X轴/Y轴/…, 最终取最大值即可;

给定若干个点, 求任意两点的曼哈顿距离的最大值

代码

template< class _TypePoint_> class ___MaximalManhattanDistance_OfOnePairPoints{
public:
    _TypePoint_ __Max_sum, __Min_sum;
    _TypePoint_ __Max_dif, __Min_dif;
    std::pair<_TypePoint_, _TypePoint_> __ANS_point[4]; // 分别对应`Max_sum, Min_sum, Max_dif, Min_dif`所表示*点坐标*;
    void Initialize(){
        __Max_sum = std::numeric_limits<_TypePoint_>::lowest();
        __Min_sum = std::numeric_limits<_TypePoint_>::max();
        __Max_dif = std::numeric_limits<_TypePoint_>::lowest();
        __Min_dif = std::numeric_limits<_TypePoint_>::max();
    }
    void Initialize_addPoint( _TypePoint_ _x, _TypePoint_ _y){
        if( _x+_y > __Max_sum){
            __Max_sum = _x+_y;
            __ANS_point[0] = {_x, _y};
        }
        if( _x+_y < __Min_sum){
            __Min_sum = _x+_y;
            __ANS_point[1] = {_x, _y};
        }
        if( _x-_y > __Max_dif){
            __Max_dif = _x-_y;
            __ANS_point[2] = {_x, _y};
        }
        if( _x-_y < __Min_dif){
            __Min_dif = _x-_y;
            __ANS_point[3] = {_x, _y};
        }
    }
    std::tuple<_TypePoint_, std::pair<_TypePoint_,_TypePoint_>, std::pair<_TypePoint_,_TypePoint_> >  Work(){
        if( __Max_sum-__Min_sum > __Max_dif-__Min_dif){
            return {__Max_sum-__Min_sum, __ANS_point[0], __ANS_point[1]};
        }
        return {__Max_dif-__Min_dif, __ANS_point[2], __ANS_point[3]};
    }
}; // ___MaximalManhattanDistance_OfOnePairPoints

定义

因为曼哈顿距离 可以转换为 切比雪夫距离, 设任一点X 他对应的切比雪夫坐标为X1 = (X.x+X.y, X.x-X.y), 那么若干个X点的最大曼哈顿距离 就等于 若干个对应的X1点的最大切比雪夫距离;
. 因此答案是max{ (X1.x最大值 - X1.x最小值), (X1.y最大值 - X1.y最小值)} (即在各个维度独立的 求一下最大值和最小值即可);

给定若干个点, 选择删除任一点后 求任意两点的曼哈顿距离的最大值的最小值

@LINK: https://editor.csdn.net/md/?not_checkout=1&articleId=137246555;

应用

@LINK: https://www.luogu.com.cn/problem/P5098;
给定若干个点, 求任意两点的曼哈顿距离的最大值; 模板题;

切比雪夫距离

定义

二维: 切比雪夫距离(A,B) = max{ abs(A.x - B.x), abs(A.y - B.y)};
. 同时他也等于曼哈顿距离(A1,B1), 其中A1 = ((A.x+A.y)/2, (A.x-A.y)/2); B1 = ((B.x+B.y)/2, (B.x-B.y)/2);

三维: 切比雪夫距离(A,B) = max{ abs(A.x - B.x), abs(A.y - B.y), abs(A.z - B.z)};

算法

给定若干个点, 求任意两点的切比雪夫距离的最大值

令X: 所有点的x坐标, Y: 所有点的y坐标, 则{ (X最大值 - X.最小值), (Y最大值 - Y.最小值)}的最大值 便是答案;