Laplace变换-2

回忆：函数$f(t)$的单边Laplace变换是以$s$为自变量的函数$$[Lf](s):={\int }_0^{\infty }{e}^{-st}f(t)dt.$$
此处假设上述反常积分收敛.

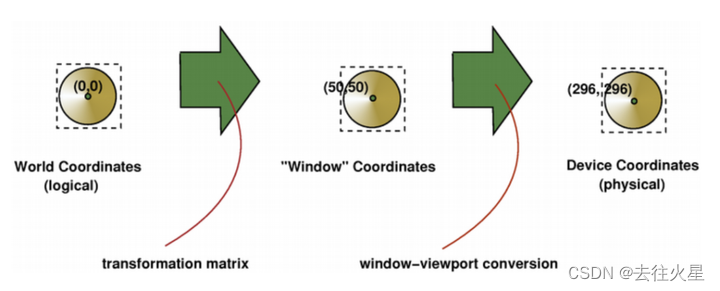
（物理）背景：$t$是时间，$s$是频率。如果$x=f(t)$表示质点（物体）在时间$t$的位置，则$z=[Lf](s)$描述质点在相空间(phase space)的状态。

#Laplace变换的性质

1. 线性：$[L({\sum }_{i=1}^k{c}_i{f}_i)](s)={\sum }_{i=1}^k{c}_i[L{f}_i](s)$.
2. 平移性质：如果$f(t)$的Laplace变换是$F(s)=[Lf](s)$. 那么$e^{at}f(t)$的Laplace变换是$F(s-a)$. （此处假设$F(s)$的定义域是$s>s_0$, 则这个性质对任意$a<s-s_0$成立）
3. 平移性质2：$f(t-t_0)\cdot H(t-t_0)$的Laplace变换是$e^{-t_{0}s}F(s)$. 这里$H(t-t_0)$当$t\ge t_0$时等于1，否则等于0. 称$H(t-t_0)$为Heaviside函数.
4. 对$-F(s)$求导会得到$tf(t)$的变换：$-\frac{d}{ds}F(s)=[L(tf(t))]$.
5. 导函数的变换：对任意$n\in \mathbb{N}$, 有$$[L{f}^{(n)}](s)=s^n[Lf](s)-s^{n-1}f(0)-s^{n-2}{f}^{\prime }(0)-\cdots -s{f}^{(n-2)}(0)-f^{(n-1)}(0).$$
6. 原函数的变换：$$[L({\int }_0^{t}f)](s)=\frac{1}{s}[Lf](s).$$ 注意：如果认为求原函数是求$-1$次导数，则4也可以认为是3中取$n=-1$.