逻辑回归(Logistic Regression)

一、分类问题

在接下来的内容中将开始介绍分类问题，在分类问题中，我们要预测的变量 y 是离散的值，我们将学习一种叫做逻辑回归 (Logistic Regression) 的算法，这是目前使用最广泛的一种学习算法。分类问题的例子有：判断一封电子邮件是否是垃圾邮件、判断肿瘤是恶性的还是良性的等等。

简单起见，我们从二元的分类问题开始讨论。我们将因变量可能属于的两个类分别称为负向类和正向类，则因变量 $y\in { 0,1 \\}$ ，其中 0 表示负向类，1 表示正向类，但如果你使用的是线性回归算法，那么假设函数的输出值可能远大于 1，或者远小于0，即使所有训练样本的标签 y 都等于 0 或 1，尽管我们知道标签应该取值0 或者1，但是如果算法得到的值远大于1或者远小于0的话，就会感觉很奇怪。所以我们在接下来的要研究的算法就叫做逻辑回归算法，这个算法的性质是：它的输出值永远在0到 1 之间。

顺便说一下，逻辑回归算法是分类算法，我们将它作为分类算法使用，有时候可能因为这个算法的名字中出现了“回归”使你感到困惑，但逻辑回归算法实际上是一种分类算法，它适用于标签 y 取值离散的情况，如：1 0 0 1。在接下来的内容中，我们将开始学习逻辑回归算法的细节。

二、假说表示

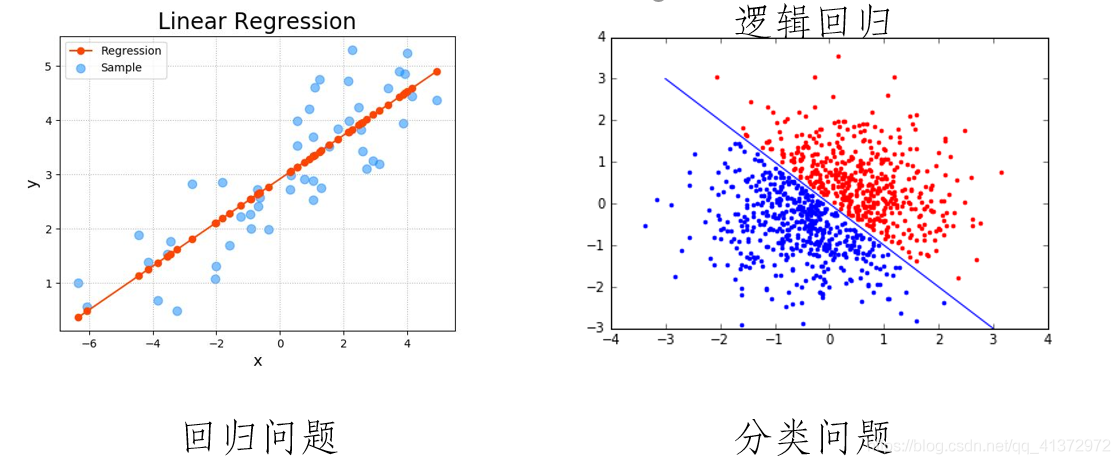
在这一小节中，我要给你们讲解假设函数的表达式，也就是说，在分类问题中，要用什么样的函数来表示我们的假设。此前我们说过，希望我们的分类器的输出值在0和1之间，因此我们希望得到一个满足某个性质的假设函数，这个性质是它的预测值要在0和1之间。回顾在一开始提到的乳腺癌分类问题，我们可以用线性回归的方法求出适合数据的一条直线：

根据线性回归模型我们只能预测连续的值，对于分类问题，我们需要输出0或1，我们可以预测：

当 ${h_\theta}\left( x \right)$ $\geq$ 0.5时，预测 y=1

当 ${h_\theta}\left( x \right)$ $<$ 0.5时，预测 y=0

对于上图所示的数据，这样的一个线性模型似乎能很好地完成分类任务。假使我们又观测到一个非常大尺寸的恶性肿瘤，将其作为实例加入到我们的训练集中来，这将使得我们获得一条新的直线。

这时再使用0.5作为阀值来预测肿瘤是良性还是恶性便不合适了，可以看出，因为线性回归模型预测的值可以超越[0,1]的范围，所以其并不适合解决这样的问题，因此我们引入一个新的模型----逻辑回归，该模型的输出变量范围始终在0和1之间。

逻辑回归模型的假设： $h_\theta \left( x \right)=g\left(\theta^{T}X \right)$

X 代表特征向量

g 代表逻辑函数（logistic function)是一个常用的逻辑函数，也叫做S形函数（Sigmoid function），公式为： $g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$

python代码实现：

import numpy as np
    
def sigmoid(z):
    
   return 1 / (1 + np.exp(-z))

该函数的图像为：

综上所述，我们得到逻辑回归模型的假设：

对模型的理解： $g\left( z \right)=\frac{1}{1+{{e}^{-z}}}$ 。

$h_\theta \left( x \right)$ 的作用是，对于给定的输入变量，根据选择的参数计算输出变量=1的可能性，即 $h_\theta \left( x \right)=P\left( y=1|x;\theta \right)$ 。例如，如果对于给定的x，通过已经确定的参数计算得出 $h_\theta \left( x \right)=0.7$ ，则表示有70%的几率y为正向类，相应地y为负向类的几率为1-0.7=0.3。

三、决策边界

现在讲下决策边界(decision boundary)的概念，这个概念能更好地帮助我们理解逻辑回归的假设函数在计算什么。

在逻辑回归中，我们预测：

当 $h_\theta \left( x \right)$ $\geqslant$ 0.5时，预测 y=1

当 $h_\theta \left( x \right)$ $<$ 0.5时，预测 y=0

根据上面绘制出的 S 形函数图像，我们知道当z=0时：g(z)=0.5；当z>0时：g(z)>0.5；当z<0时：g(z)<0.5。又 $z={\theta^{T}}x$ ，即： ${\theta^{T}}x$ $\geq$ 0 时，预测 y=1； ${\theta^{T}}x$ $<$ 0 时，预测 y=0

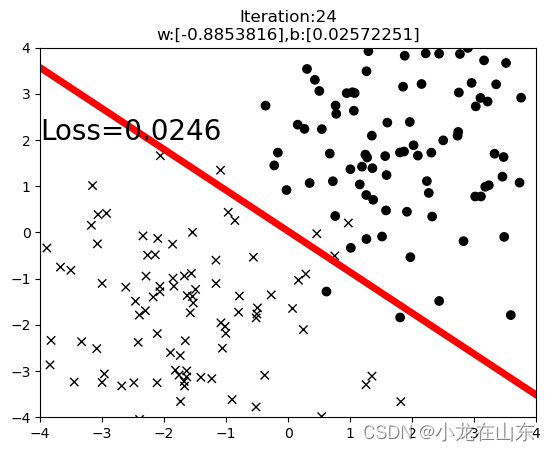
现在假设我们有一个模型，并且参数 $\theta$ 是向量[-3 1 1]，则当 $-3+{x_1}+{x_2} \geq 0$ ，即 ${x_1}+{x_2} \geq 3$ 时，模型将预测 y=1。我们可以绘制直线 ${x_1}+{x_2} = 3$ ，这条线便是我们模型的分界线，将预测为1的区域和预测为 0的区域分隔开。

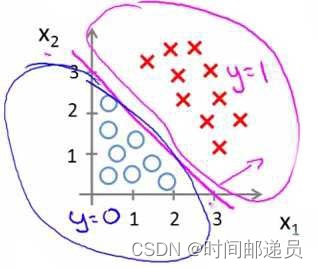
又假如我们的数据呈现这样的分布情况，怎样的模型才能适合呢？

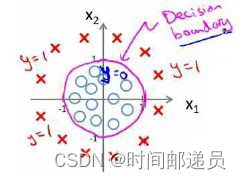
因为需要用曲线才能分隔 y=0 的区域和 y=1 的区域，我们需要二次方特征，即 ${h_\theta}\left( x \right)=g\left( {\theta_0}+{\theta_1}{x_1}+{\theta_{2}}{x_{2}}+{\theta_{3}}x_{1}^{2}+{\theta_{4}}x_{2}^{2} \right)$ ，并且参数 $\theta$ 是向量[-1 0 0 1 1]，则我们得到的判定边界恰好是圆点在原点且半径为1的圆形，因此我们可以用非常复杂的模型来适应非常复杂形状的判定边界。

四、代价函数

在这一小节中，我们要介绍如何拟合逻辑回归模型的参数 $\theta$ 。具体来说，我要定义用来拟合参数的优化目标或者叫代价函数，这便是监督学习问题中的逻辑回归模型的拟合问题。

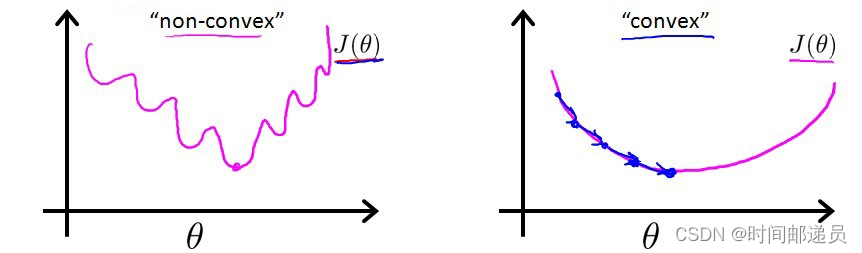
对于线性回归模型，我们定义的代价函数是所有模型误差的平方和。理论上来说，我们也可以对逻辑回归模型沿用这个定义，但是问题在于当我们将 ${h_\theta}\left( x \right)=\frac{1}{1+{e^{-\theta^{T}}X}}$ 带入到这样的代价函数中时，我们得到的代价函数将是一个非凸函数（non-convexfunction）似乎国外的凸函数和我们理解的不一样，这意味着我们的代价函数有许多局部最小值，这将影响梯度下降算法寻找全局最小值

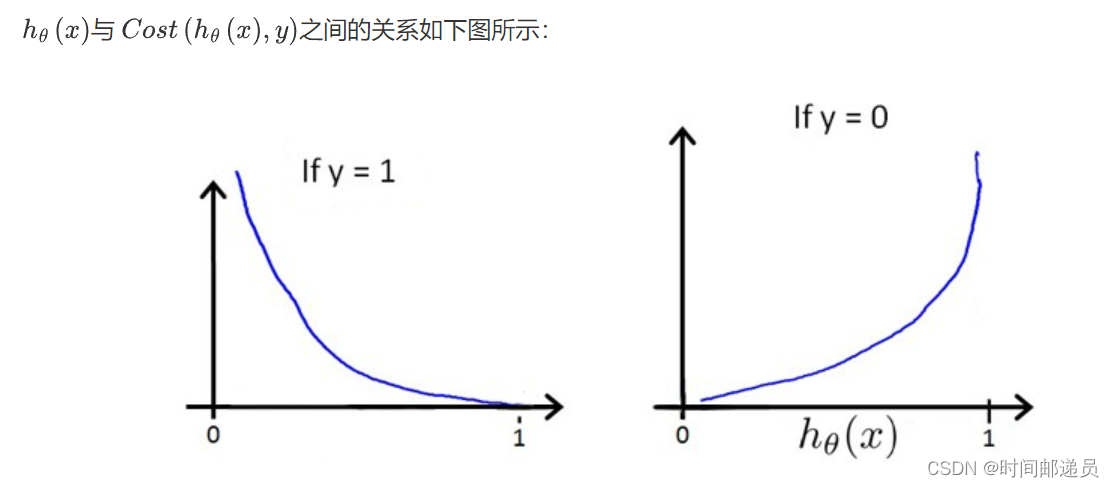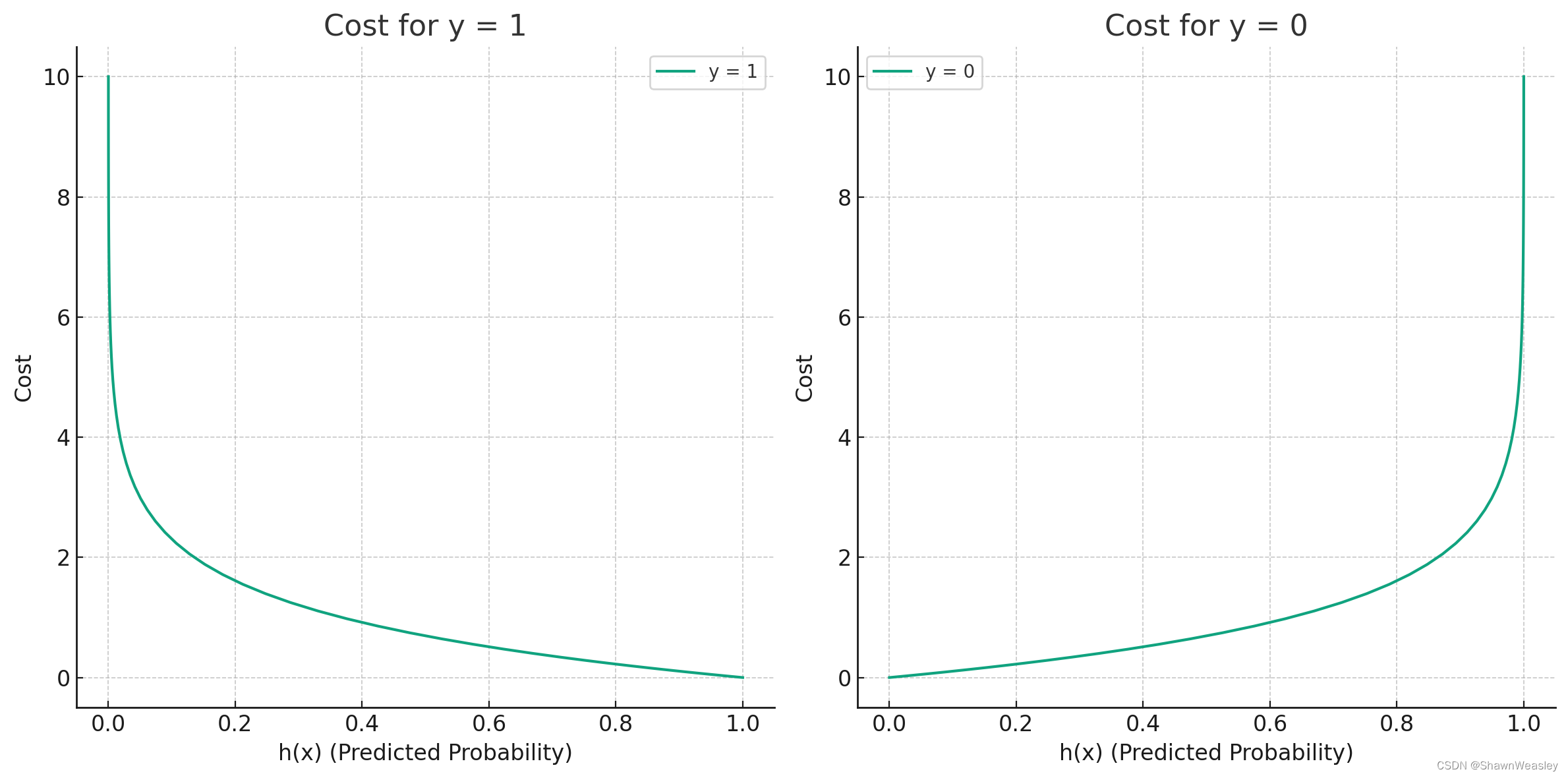
这样构建的 $Cost\left( {h_\theta}\left( x \right),y \right)$ 函数的特点是：当实际的 y=1 且 ${h_\theta}\left( x \right)$ 也为 1 时误差为 0，当 y=1 但 ${h_\theta}\left( x \right)$ 不为1时误差随着 ${h_\theta}\left( x \right)$ 变小而变大；当实际的 y=0 且 ${h_\theta}\left( x \right)$ 也为 0 时代价为 0，当y=0 但 ${h_\theta}\left( x \right)$ 不为 0时误差随着 ${h_\theta}\left( x \right)$ 的变大而变大。

将构建的 $Cost\left( {h_\theta}\left( x \right),y \right)$ 简化如下：

带入代价函数得到：

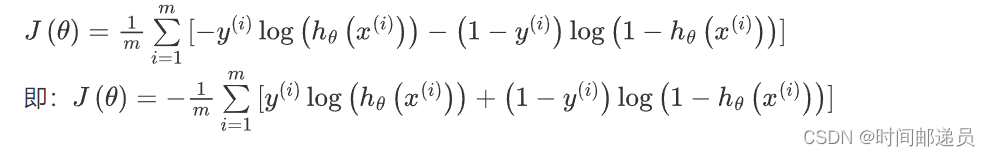
Python代码实现：

import numpy as np
    
def cost(theta, X, y): 
  theta = np.matrix(theta)
  X = np.matrix(X)
  y = np.matrix(y)
  first = np.multiply(-y, np.log(sigmoid(X* theta.T)))
  second = np.multiply((1 - y), np.log(1 - sigmoid(X* theta.T)))
  return np.sum(first - second) / (len(X))

在得到这样一个代价函数以后，我们便可以用梯度下降算法来求得能使代价函数最小的参数了,算法为：

求偏导后得到：

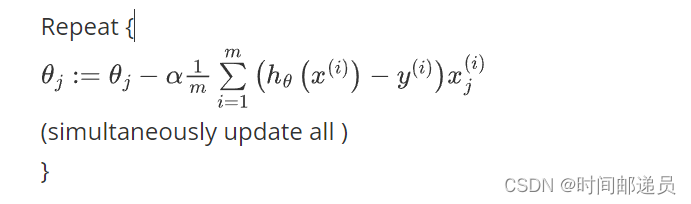大家会发现，虽然得到的梯度下降算法表面上看上去与线性回归的梯度下降算法一样，但是这里的 ${h_\theta}\left( x \right)=g\left( {\theta^T}X \right)$ 与线性回归中不同，所以实际上是不一样的。另外在运行梯度下降算法之前，进行特征缩放依旧是非常必要的。

五、多类别分类：一对多

在本小节内容中，我们将谈到如何使用逻辑回归 (logistic regression)来解决多类别分类问题，具体来说，我想实现一个叫做"一对多" (one-vs-all) 的分类算法，先看这样一些例子。

第一个例子：假如说你现在需要一个学习算法能自动地将邮件归类到不同的文件夹里，或者说可以自动地加上标签，那么你也许需要一些不同的文件夹或者不同的标签来完成这件事，区分开来自工作的邮件、来自朋友的邮件、来自家人的邮件或者是有关兴趣爱好的邮件，那么我们就有了这样一个分类问题：其类别有四个，分别用y=1、y=2、y=3、y=4 来代表。

第二个例子是有关药物诊断的，如果一个病人因为鼻塞来到你的诊所，他可能并没有生病，用 y=1 这个类别来代表；或者患了感冒，用 y=2 来代表；或者得了流感用y=3来代表。

对于之前的一个二元分类问题，我们的数据看起来可能是像这样：

对于一个多类分类问题，我们的数据集或许看起来像这样：

我用三种不同的符号来代表三个类别，问题就是给出三个类型的数据集，我们如何得到一个学习算法来进行分类呢？我们现在已经知道如何进行二元分类，可以使用逻辑回归，对于直线或许你也知道，可以将数据集一分为二为正类和负类。用一对多的分类思想，我们可以将其用在多类分类问题上。下面将介绍如何进行一对多的分类工作，有时这个方法也被称为"一对余"方法。

现在我们有一个训练集，好比上图表示的有三个类别，我们用三角形表示 y=1，方框表示y=2，叉叉表示 y=3。我们下面要做的就是使用一个训练集，将其分成三个二元分类问题。

我们先从用三角形代表的类别1开始，实际上我们可以创建一个新的"伪"训练集，类型2和类型3定为负类，类型1设定为正类，我们创建一个新的训练集，如下图所示的那样，我们要拟合出一个合适的分类器。

这里的三角形是正样本，而圆形代表负样本。可以这样想，设置三角形的值为1，圆形的值为0，为了能实现这样的转变，我们将多个类中的一个类标记为正向类（y=1），然后将其他所有类都标记为负向类，这个模型记作 $h_\theta^{\left( 1 \right)}\left( x \right)$ 。接着类似地我们选择另一个类标记为正向类（y=2），再将其它类都标记为负向类，将这个模型记作 $h_\theta^{\left( 2 \right)}\left( x \right)$ 。依此类推。最后我们得到一系列的模型简记为： $h_\theta^{\left( i \right)}\left( x \right)=p\left( y=i|x;\theta \right)$ ，其中： $i=\left( 1,2,3....k \right)$

最后为了做出预测，我们给出输入一个新的 x 值。我们要做的就是在我们三个分类器里面输入 x，然后我们选择一个让 $h_\theta^{\left( i \right)}\left( x \right)$ 最大的 i，即 $\mathop{\max}\limits_i\,h_\theta^{\left( i \right)}\left( x \right)$