这是二分法的第19篇算法,力扣链接。
给你一个
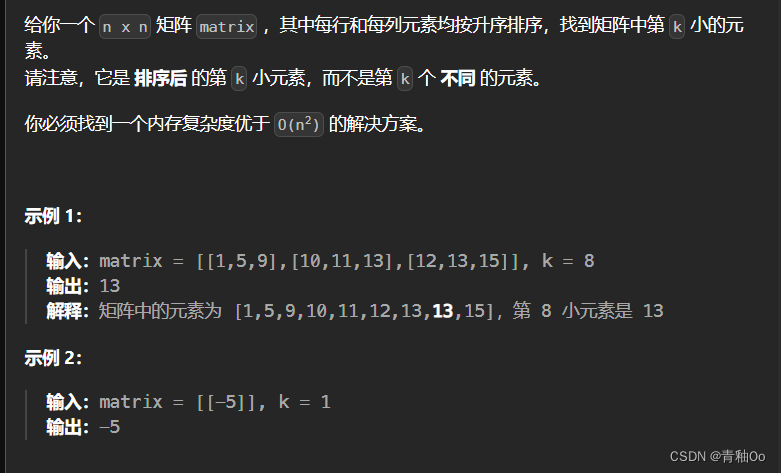
n x n矩阵matrix,其中每行和每列元素均按升序排序,找到矩阵中第k小的元素。
请注意,它是 排序后 的第k小元素,而不是第k个 不同 的元素。你必须找到一个内存复杂度优于
O(n2)的解决方案。示例 1:
输入:matrix = [[1,5,9],[10,11,13],[12,13,15]], k = 8 输出:13 解释:矩阵中的元素为 [1,5,9,10,11,12,13,13,15],第 8 小元素是 13
这道题很抽象,他告诉我们行和列都是有序的。但是不代表下一列一定大于上一行。
老规矩,直接上暴力法,先把所有数字存起来然后排序。
func kthSmallest(matrix [][]int, k int) int {
nums := make([]int, len(matrix)*len(matrix[0]))
index := 0
for _, row := range matrix {
for _, num := range row {
nums[index] = num
index++
}
}
sort.Ints(nums)
return nums[k-1]
}那这道题二分法怎么搞呢?
首先明确,无论这个分布怎么诡异,在matrix[0][0]的数一定matrix[len(matrix)-1][len(matrix[0])-1]的数小。我门可以利用这两个值当作边界,往中间找mid,移动左右边界的逻辑可以根据小于等于mid的数的多少。当左右指针相等的时候返回指针就可以了。
这时候还会有一个疑问,当左右指针相等的时候,那个边界的值真的存在吗,这个值不是根据mid左右移动算出来的吗。
其实很简单,求出矩阵元素排序后,把矩阵分成两份,且使得前一份包含k个元素的数值范围左边界值(满足条件的数值可能是个范围,有些值不存在矩阵中,但这个左边界值一定在矩阵中)。可以尝试去推导一下,会发现这个结论是存在的。
上代码:
func kthSmallest(matrix [][]int, k int) int {
l, r := matrix[0][0], matrix[len(matrix)-1][len(matrix[0])-1]
for l <= r {
mid := l + (r-l)/2
if count(mid, matrix) < k {
l = mid + 1
} else {
r = mid - 1
}
}
return l
}
func count(mid int, matrix [][]int) int {
result, x, y := 0, len(matrix)-1, 0
for x >= 0 && y < len(matrix[0]) {
if matrix[x][y] <= mid {
result += x + 1
y++
} else {
x--
}
}
return result
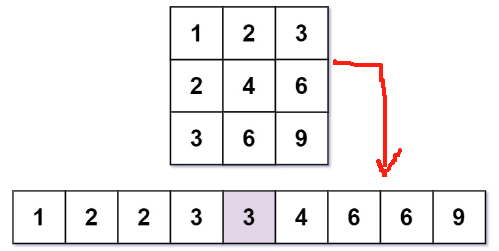
}这个count是有点学问的,这个是一列一列的加数字,梯形的方式加。
























![3.[BUU]warmup_csaw_20161](https://img-blog.csdnimg.cn/direct/dcc6fe8ea7f04cdf9b94a4a732a85cde.png)
![[已解决] Ubuntu远程桌面闪退+登录显示“远程桌面由于数据加密错误 , 这个会话将结束“](https://img-blog.csdnimg.cn/direct/81e8a3d0d68d42f198e02d333cc0c9ad.png)