截痕法分析曲面形状@旋转曲面@双曲面@锥面

abstract

• 使用截痕法分析曲面形状
  • 旋转曲面方程及其特点
• 伸缩变形法另见它文:
  • 空间曲面@曲面分析方法@常见曲面方程@球面@柱面@二次曲面分类和汇总

旋转曲面👺

基本概念

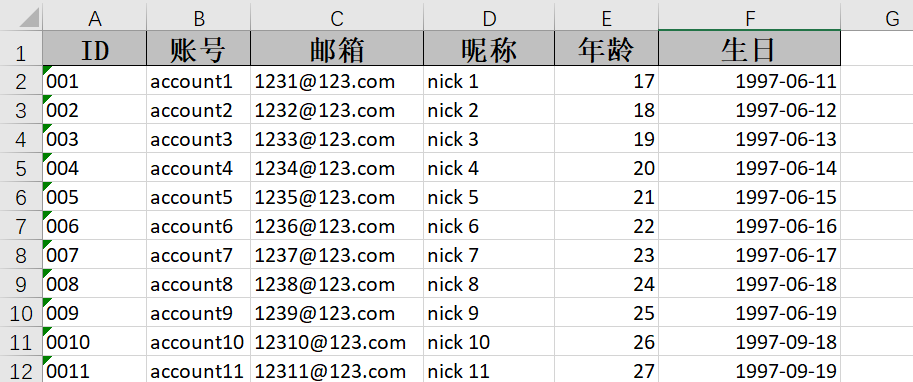
• 以一条平面曲线$C$绕其平面上的一定直线旋转一周所成的曲面称为旋转曲面

• 旋转曲线$C$称为旋转曲面的母线,定直线称为旋转曲面的轴

• 平面曲线(绕坐标轴)旋转类曲面的共同特点是可以利用几何关系:曲线上的各点在旋转过程中旋转半径恒定

• 某个点的相对于其旋转轴的距离(旋转半径)的计算可以使用2点坐标的距离公式计算

• 为了建立旋转后的点所满足的方程(面由点构成,因此曲面上的点满足的方程也是旋转曲线后构成的曲面的方程)

  • 设曲线C若属于某个坐标面,该平面包含的两个坐标轴记为$u_1,u_2$,另一个轴是该平面的法线方向,记为$u_0$
  • 设已知曲线上的点$M_1=(x_1,y_1,z_1)$坐标满足曲线方程$C:f(u_1,u_2)=0$(曲线方程仅包含变量$u_1,u_2$,因为$u_0=0$在坐标面$u_{1}O{u}_2$上是恒定的)
  • 将旋转后的点的坐标记为$M=(x,y,z)$,其中,$M$在旋转轴坐标轴$u_0$上的坐标分量和$M_1$的相同,记为$u_0(M)=u_0(M_1)$,其中函数$u_0(M)$表示计算点$M$在$u_0$轴上的坐标分量(即投影),可以类似地定义$u_1(M),u_2(M)$分别表示点M在$u_1,u_2$轴上的投影

旋转情况分类

• 绕$u_1$轴旋转

  • 坐标面上曲线C:$f(u_1,u_2)=0;u_0=0$上的点$M_1(u_0(M_1),u_1(M_1),u_2(M_1))$在旋转过程中的轨迹所在平面和$u_{0}O{u}_2$平行
  • 根据勾股定理,可以确定$M_1,M$在非旋转轴2个坐标轴上的坐标的关系为:平方和相等,记为$u_0(M{)}^2+u_2(M{)}^2=u_0(M_1{)}^2+u_2(M_1{)}^2$
  • 设曲线$C$属于平面$u_{1}O{u}_2$,从而$u_0(M_1)=0$,即$u_0(M{)}^2+u_2(M{)}^2=u_2(M_1{)}^2$仅根据这个关系,我们还无法得到能够完整描述$M$的各个坐标分量的关系(方程),需要借助曲线$C$的方程$C:f(u_1,u_2)=0$
    • 由于点$M_1$在$C$上,成立$D:f(u_1(M_1),u_2(M_1))=0$
    • $u_2(M_1)=\pm \sqrt{u_0(M{)}^2+u_2(M{)}^2}$
    • $u_1(M)=u_1(M_1)$,即$u_1(M_1)=u_1(M)$
    • 方程$D$,得到$f(u_1(M),\pm \sqrt{u_0(M{)}^2+u_2(M{)}^2})=0$,也就是关于点$M$的三个坐标分量的关系方程(作为旋转曲面的方程)

• 类似的,可以讨论绕$u_2$轴旋转的情况

例

• 以yOz上的曲线绕$z$轴旋转为例

• 设在$yOz$坐标面上有曲线$C:f(y,z)=0$

• 把$C$绕$z$轴旋转一周,得到一个以$z$轴为轴的旋转曲面,它的方程的构造:

  • 设$M_1(0,y_1,z_1)$是曲线$C$上的一点(位于坐标面$yOz$),有$f(y_1,z_1)=0$成立

  • 当$C$绕$z$轴旋转时,点$M_1$绕$z$轴转到另一点$M(x,y,z)$

  • 此时$z=z_1$

  • 同时点$M$,到$z$轴的距离,$d=\sqrt{x^2+y^2}=\sqrt{0^2+y_1^2}=|y_1|$,此时$y_1=\pm d=\pm \sqrt{x^2+y^2}$

  • 将$z_1,y_1$带入到$f(y_1,z_1)=0$,即$f(\pm \sqrt{x^2+y^2},z)=0$

旋转曲面的方程👺

研究思路

• 曲面方程就是描述曲面上所有点的坐标满足的关系式(方程式)
  • 因此,我们可以任意取曲面上的某个点$P(x,y,z)$进行研究,得到关于$x,y,z$的方程
• 旋转曲面由其母线和旋转轴唯一确定,因此旋转曲面的方程和母线方程有密切联系
  • 我们考虑将旋转曲面上的任意点$P$和母线上的某点$P_1$联系起来,利用母线上的点满足母线方程的事实来得到曲面方程
  • 即,可以通过研究旋转曲面的母线$C$上的任意一点在旋转过程中形成的轨迹方程来得到旋转曲面的方程

推导过程

• 以$yOz$平面(即$x=0$平面)上的曲线$C:f(y,z)=0$绕$z$轴旋转一周得到的旋转曲面方程推导为例
  • 设$P(x,y,z)$是旋转曲面$\Pi$上的任意一点,该曲面由$yOz$坐标面上的曲线$C$作为旋转母线绕$z$轴旋转一周得到的,设$C$的方程为$f(y,z)=0;x=0$(0)
  • 显然,点$P(x,y,z)$可看作是由曲线$C$上的某点$P_1(0,y_1,z_1)$(0-1)旋转得到
    • $P,P_1$具有相同的$z$轴坐标,即$z_1=z$(1),并且$P_1$是$yOz$面(即$x=0$平面)上的点,因此$P_1$的$x$轴坐标为0,因此这里直接设$P_1(0,y_1,z_1)$
    • 另一方面,$P(x,y,z)$在$xOy$面上的投影坐标为$Q(x,y)$由旋转关系可知,$x^2+y^2$=$y_1^2$(2),即$y_1=\pm \sqrt{x^2+y^2}$(2-1)
    • 而$P_1$满足曲线$C$的方程,即$f(y_1,z_1)=0$(3),将式(1,2-1)代入(3),得$f(\pm \sqrt{x^2+y^2},z)=0$(1),此方程描述了旋转曲面上任意点满足的方程,即旋转曲面的方程
• 类似的,若旋转曲面是曲线$C$绕着$y$轴旋转,得到的旋转曲面方程为$f(y,\pm \sqrt{x^2+z^2})=0$(2)

小结

• 方程公式(1,2)都包含了$x,y,z$三个变量
• 以$yOz$平面(即$x=0$坐标面)内曲线方程$f(y,z)=0$(1);$x=0$例
  • 以$y$轴为旋转轴时,公式(1)中字母$y$(称为转轴字母)就保持不变,而把另一个字母$z$替换为转轴字母以外的两个字母的平方和开根号,对于(1)式就是将字母$z$替换为根式$\delta (y)$=$\pm \sqrt{x^2+z^2}$,记为$\overline{y}\to \delta (y)=\pm \sqrt{x^2+z^2}$替换(这里用$\overline{y}$表示方程(1)中转轴字母外的字母,即$z$,这就得到$f(y,\pm \sqrt{x^2+z^2})=0$这一旋转面公式
  • 若绕着$z$轴旋转,则类似的替换:$\overline{z}\to \delta (z)=\pm \sqrt{x^2+y^2}$
• 其他坐标面上的图形绕轴旋转的公式情形类似,将上述公式整理并补充如下
  • $x=0$面内的曲线$f(y,z)=0,x=0$,绕$y$轴旋转:$f(y,\pm \sqrt{x^2+z^2})=0$;绕$z$轴旋转:$f(\pm \sqrt{x^2+y^2},z)=0$
  • $y=0$面内的曲线$f(x,z)=0,y=0$绕$x$轴旋转:$f(x,\pm \sqrt{y^2+z^2})$=0;绕$z$轴旋转:$f(\pm \sqrt{x^2+y^2},z)$=0
  • $z=0$面内的曲线$f(x,y)=0,z=0$绕$x$轴旋转:$f(x,\pm \sqrt{y^2+z^2})=0$;绕$y$轴旋转:$f(\pm \sqrt{x^2+z^2},y)=0$

常见旋转曲面方程

• $yOz$面上抛物线$C:y^2=2pz$(1)绕$z$轴旋转所成的曲面方程为$x^2+y^2=2pz$(1-1),这类曲线称为旋转抛物面
• $yOz$面上椭圆线$C:\frac{y^2}{a^2}+\frac{z^2}{b^2}=1$(2)绕$z$轴旋转所成的曲面方程为$\frac{x^2+y^2}{a^2}+\frac{z^2}{b^2}=1$,(2-1),这类曲线称为旋转椭圆面
• $xOz$面上双曲线$C:\frac{x^2}{a^2}-\frac{z^2}{b^2}=1$(3)绕$z$轴,$x$轴旋转所成的曲面方程分别为$\frac{x^2+y^2}{a^2}-\frac{z^2}{b^2}=1$(3-1),$\frac{x^2}{a^2}-\frac{y^2+z^2}{b^2}=1$(3-2),这两类曲线分别称为旋转单叶双曲面,旋转双叶双曲面

双曲面

单叶双曲面

• 方程(3-1)也写作:$\frac{x^2}{a^2}+\frac{y^2}{a^2}-\frac{z^2}{b^2}=1$,
• 更一般的单叶双曲面$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$(4)(当$a^2=b^2$时是绕$z$轴的旋转面,类似可以写出其他轴的情形)

  • 将(4)变形为:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=$1+\frac{z^2}{c^2}$(4-1)

  • 利用截面$z=z_0$去截(4),若式(4)中若$a^2\ne b^2$,可得截面方程为椭圆,若$a^2=b^2$,则截得一个圆(此时式(4)是旋转单叶双曲面)

    • (4-1)两边同时除以$1+\frac{z^2}{c^2}$,得到椭圆标准式

  • 利用截面$x=x_0$,$y=y_0$截方程(4),得到的都是双曲线的方程

    • 以$x=0$为例,得到$\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$,(当$b=c$也是双曲线)

双叶双曲面

• 形如:$\frac{x^2}{a^2}-\frac{y^2}{b^2}-\frac{z^2}{c^2}=1$(5)或写成$\frac{y^2}{b^2}+\frac{z^2}{c^2}-\frac{x^2}{a^2}=-1$(5-1)(当$b^2=c^2$时是绕$x$轴旋转面)
• 将(5-1)变形为$\frac{y^2}{b^2}+\frac{z^2}{c^2}$=$\frac{x^2}{a^2}-1$(5-2)
• 首先分析自变量取值范围
  • 式(5-2)左端为非负的,所以右端非负,即$\frac{x^2}{a^2}-1⩾0$,从而$x^2⩾a^2$,即$|x|⩾|a|$
  • 这意味着$(-|a|,|a|)$区间内曲面没有定义
  • 而用$|x|⩾|a|$范围内的$x=x_0$去截取(5-2),
    • 若$b^2\ne c^2$,则得到的方程是椭圆方程
    • 若$b^2=c^2$,则得到圆,此时方程(5)是旋转曲面
  • 用$y=y_0$或$z=z_0$截得的截痕方程都是双曲线
  • 综上,这就容易勾勒出双叶双曲面的空间图形

双曲抛物面(马鞍面)

• 形如$\frac{x^2}{a^2}-\frac{y^2}{b^2}=z$(6)
  • 分别用$z=z_0$,$x=x_0$,$y=y_0$去截曲面(6)
  • 截痕分别为双曲线,抛物线(开口朝$z$轴负方向),抛物线(开口朝$z$轴正方向)

锥面👺

• 移动直线$L$,使它始终通过点$Q$且始终与定曲线$C$相交,这样由$L$所生成的曲面叫做锥面
• 特征:顶点与曲面上任意其他点的连线都在曲面上,若顶点在原点,则顶点与锥面上一点$P(x,y,z)$的连线直线$L$方程的参数方程可知,$L$上任意点$T$可以表示为$(tx,ty,tz)$,$t$可以为任意实数
• 因此若$P(x,y,z)$满足$f(x,y,z)=0$,则$T(tx,ty,tz)$也满足$f(x,y,z)=0$
• 例如,令$f(x,y,z)$=$\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2}$,方程$f(x,y,z)=0$
  • 容易验证$f(tx,ty,tz)$=$\frac{t^2{x}^2}{a^2}+\frac{t^2{y}^2}{b^2}-\frac{t^2{z}^2}{c^2}$=$t^2(\frac{x^2}{a^2}+\frac{y^2}{b^2}-\frac{z^2}{c^2})$=0
• 构造锥面(二次曲线)
  • $f(x,y,z)$=$a{x}^2+b{y}^2+c{z}^2$(1),$f(tx,ty,tz)$=$t^{2}f(x,y,z)$
  • 若$f(x,y,z)=0$,则$f(tx,ty,tz)$=0,因此形如$a{x}^2+b{y}^2+c{z}^2=0$的方程都是锥面
  • 例如$G(x,y,z)$=$t^2(x^2-y^2+z^2)$=$(tx{)}^2-(ty{)}^2+(tz{)}^2$;$f(x,y,z)=x^2-y^2+z^2$
• 锥面的截面图形
  • 用平面$x=0$去截锥面,可得$y^2=z^2$,即$z=y$或$z=-y$,这在坐标面$yOz$(即$x=0$平面)上表现为过原点的直线,并且两条直线关于$z$轴对称
  • 类似的$y=0$去截锥面由类似效果